





Preview text:
Sản phẩm của: “Nhóm Toán Tiểu Học-THCS-THPT VIỆT NAM”
LỜI GIẢI ĐƯỢC THỰC HIỆN BỞI
Tập Thể Giáo Viên Nhóm Toán “Tiểu Học – THCS – THPT VIỆT NAM”
Tạ Thị Huyền Trang Nguyễn Trí Chính Hoàng Dương Thắng Vũ Phạm Thụ Trần Lệnh Ánh Phạm Thu Hà Việt Dũng Lê Hợp Nguyễn Lan Anh Phạm Văn Tuân Lê Hường
Ngô Nguyễn Quốc Mẫn Võ Quang Mẫn Trần Hùng Quân Lê Quỳnh Trang Lê Minh Đức
Lê Thị Hoàng Hạnh Bùi Quốc Trọng Phạm Duy Nguyên Nguyễn Hưng Nguyễn Minh Toàn Bài 1. (2,5 điểm) Cho 1 5 a + = 2
a) Tìm một đa thức bậc hai Q(x) với hệ số nguyên sao cho α là nghiệm của Q(x) b) Cho đa thức: 5 4
P(x) = x − x − x +1. Tính giá trị của P(α) Lời giải
a).Tìm một đa thức bậc hai Q(x) với hệ số nguyên sao cho α là nghiệm của Q(x) Cách 1: Có 1+ 5 2 2 α =
⇔ 2α −1 = 5 ⇒ 4α − 4α − 4 = 0 ⇔ α −α −1 = 0 . 2
NHÓM TOÁN TIỂU HỌC – THCS - THPT VIỆT NAM Trang 2
Sản phẩm của: “Nhóm Toán Tiểu Học-THCS-THPT VIỆT NAM” Phương trình 2
x − x −1 = 0 có hệ số nguyên và có 2 nghiệm 1 5 α + = , 1 5 β − = . 2 2 Vậy Q(x) 2
= x − x −1 thỏa yêu cầu bài. Cách 2: Có 1 5 α + = , đặt 1 5 β − = 2 2 α + β = 1 Ta có α .β = 1 −
Phương trình có hệ số nguyên nhận α , β làm nghiệm là 2
x − x −1 = 0 Vậy Q(x) 2
= x − x −1 thỏa yêu cầu bài. b) 5 4 5 4 3 3
P(x) = x − x − x +1 = x − x − x + x − x +1 3 P x = x ( 2 x − x − ) 3 2 2 ( )
1 + x − x − x + x +1 2 3 2
P(x) = (x − x −1)(x + x) + x +1 2 3 2
P(α) = (α −α −1)(α +α) +α +1. 2
P(α) = 0 +α +1 (Do α là nghiệm của phương trình: 2 x − x −1). Mà 2 α +1 = α + 2 nên 2 1 5 5 5 P(α) α 1 α + + = + = + 2 = + 2 = . 2 2 Vậy 5 5 P(α + ) = . 2 Bài 2. (3,0 điểm) Cho ,
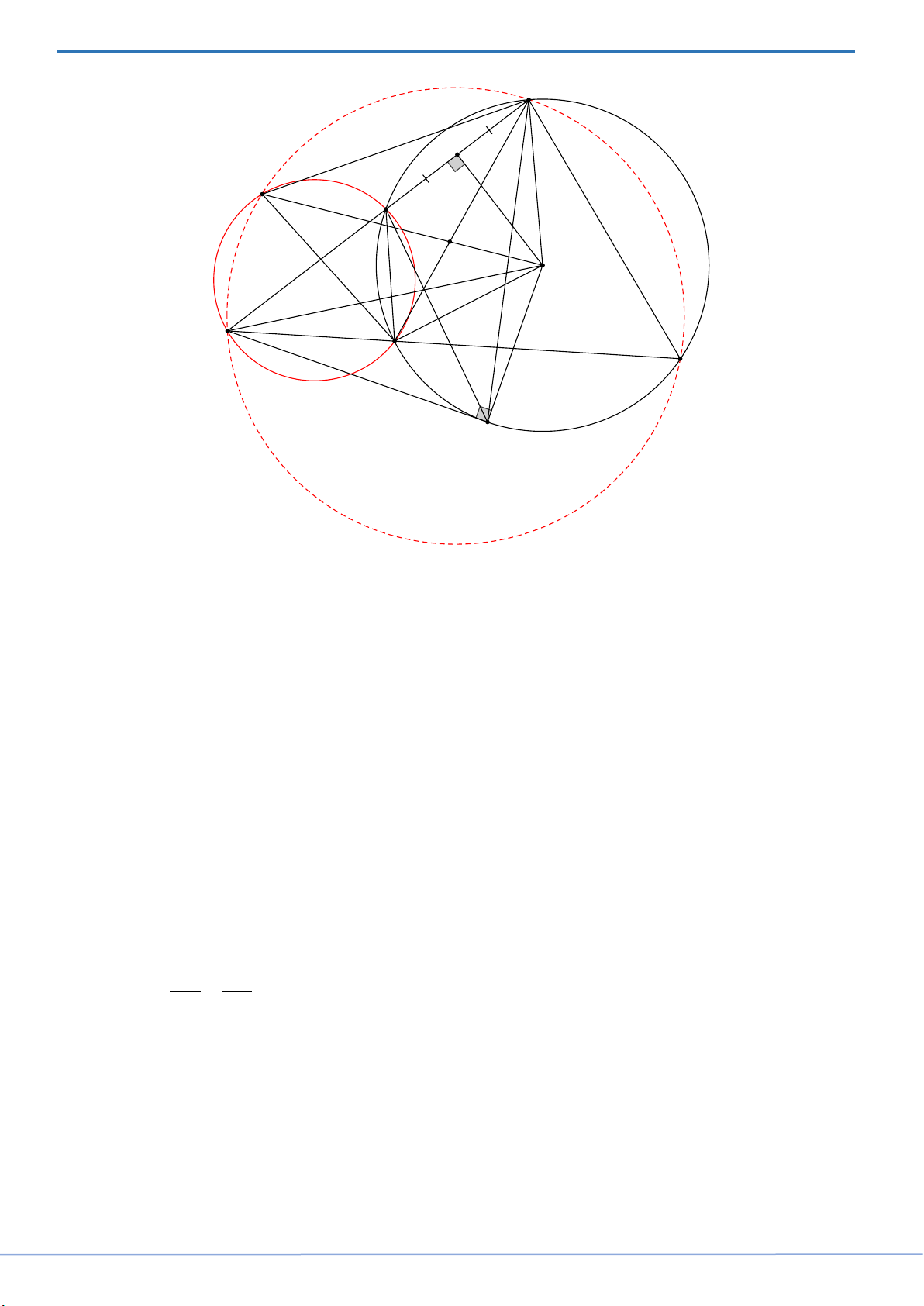
A B là hai điểm cố định nằm trên đường tròn tâm O , bán kính R . Giả sử C là điểm cố
định trên tia đối của tia BA . Một cát tuyến thay đổi qua C cắt đường tròn (O) tại D và E (
D nằm giữa C, E ). Các đường tròn ngoại tiếp các tam giác BCD và ACE cắt nhau tại giao
điểm thứ hai M . Biết rằng bốn điểm O, B,M , E tạo thành tứ giác OBME . Chứng minh rằng:
a) Tứ giác OBME nội tiếp. b) 2 2 .
CD CE = CO − R .
c) M luôn di chuyển trên một đường tròn cố định. Lời giải
NHÓM TOÁN TIỂU HỌC – THCS - THPT VIỆT NAM Trang 3
Sản phẩm của: “Nhóm Toán Tiểu Học-THCS-THPT VIỆT NAM” E T M D O C B A F
a) Chứng minh tứ giác OBME nội tiếp.
= = = = −
EOB 2BAE 2BDC 2BMC 2(EMC EMB) = ° − − 2(180 EAB EMB) = ° − − 360 EOB 2EMB suy ra +
EOB EMB =180° hay tứ giác OBME nội tiếp. b) Chứng minh 2 2 .
CD CE = CO − R . Cách 1.
Kẻ CF là tiếp tuyến của (O) , suy ra 2 2 2 2 2
CF ⊥ OF ⇒ CF = CO − OF = CO − R (1) Mặt khác: C ∆ DF ∽ C ∆ FE (g.g) CD CF 2 ⇒ = ⇒ CF = . CD CE (2) CF CE Từ (1) và (2) ta có 2 2 .
CD CE = CO − R . Cách 2.
Gọi T là trung điểm DE . Có .
CD CE = (CT −TD)(CT +TE), TD = TE 2 2 2 2 2 2 2 2 2
= CT −TD = CO − OT −TD = CO − OD = CO − R
NHÓM TOÁN TIỂU HỌC – THCS - THPT VIỆT NAM Trang 4
Sản phẩm của: “Nhóm Toán Tiểu Học-THCS-THPT VIỆT NAM”
c) Chứng minh M luôn di chuyển trên một đường tròn cố định. = + = +
OMC OMB BMC OEB EAB = 90° hay M luôn di chuyển trên đường tròn đường
kính OC cố định. Bài 3. (2,0 điểm)
Tìm tất cả các số nguyên dương N sao cho N có thể biểu diễn một cách duy nhất ở dạng 2
x y +1 với x, y là hai số nguyên dương. xy +1 Lời giải 2 x + y 2 N =
⇔ x − Nxy − N + y = 0 ⇔ x(Ny − x) = y − N ( ) 1 xy +1
Với N =1 dễ thấy có vô số cách biểu diễn N theo x, y
là các bộ số dạng (x y) = (a a + ) ( * , , 1 a ∈ ) Với N ≥ 2 Nếu 2
y = N ⇒ x = N
Nếu y ≠ N thì ( )
1 ⇒ y − Nx ⇒ y − N ≥ x
suy ra trong hai số y; N có ít nhất một số lớn hơn x
⇒ Ny − x > 0 ⇒ y − N > 0 ⇒ y > N ⇒ y > x Từ ( )
1 ⇒ y − NNy − x ⇒ y − N ≥ Ny − x ≥ 2y − x ≥ y + ( y − x) ≥ y ⇒ N ≤ 0 ( loại) 2 +
Vậy với N ≥ 2 thì ta có một biểu diễn duy nhất ở dạng x y xy +1 Cách khác. 2 x + y
+) N = 1 có vô số bộ ( ;
x y) có dạng (k;k + )
1 (k ∈ N )thỏa mãn = N . xy +1 Suy ra N =1 loại +) N ≠ 1 2 x + y xy +1 ⇒ y( 2
x + y) − x(xy + ) 1 xy +1 2
⇒ y − xxy +1
NHÓM TOÁN TIỂU HỌC – THCS - THPT VIỆT NAM Trang 5
Sản phẩm của: “Nhóm Toán Tiểu Học-THCS-THPT VIỆT NAM” +) 2
x < y ⇒ x + y ≤ xy + y < 2xy + 2 2 2 + ⇒ + ≤ + = 2 < 2 + 2 x y x y xy xy xy xy ⇒
< 2 ⇒ N < 2 vô lý. xy +1
+) x ≥ y ⇒ −( xy + ) 2 2
1 < −x < y − x < y < xy +1 2 2
⇒ y − x = 0 ⇒ x = y 4 y + y ⇒ N = = y 2 y +1 2 ⇒ x = N
Với mọi N > 1 thì cặp ( 2
N ; N ) là duy nhất Bài 4. (2,5 điểm)
Cho a , b , c là ba số nguyên dương sao cho mỗi số trong ba số đó đều biểu diễn được dưới
dạng lũy thừa của 2 với số mũ tự nhiên. Biết rằng phương trình bậc hai 2
ax − bx + c = 0 (1) có
cả hai nghiệm đều là số nguyên. Chứng minh rằng hai nghiệm của phương trình (1) bằng nhau. Lời giải Cách 1:
Đặt = 2k; = 2n; = 2m a b c (k, , m n∈)
Gọi x ; x là nghiệm nguyên của phương trình 2
ax − bx + c = 0 1 2 Ta có 2 − + = 0 ⇒ = − > 0 ⇒ ⇒ 2m ax bx c c x b ax c x
x tương tự 2mx 1 2 ( ) 1 1 1 ( 1 ) 1 1
x + x = 2n−k x > 0 Theo hệ thức Vi-et: 1 2 1 ⇒ (2)
x .x = 2m−k x > 0 1 2 2 Từ ( )
1 ;(2) ⇒ x ; x là các lũy thừa với số mũ tự nhiên của 2. 1 2
Đặt = 2p, = 2q x x p,q ∈
không mất tính tổng quát giả sử p ≥ q . 1 2 ( ) Khi đó 2n k 2q 2p q 1 2n k 2p q 1 2n k q x x − − − − − − + = ⇔ + = ⇒ + = 1 2 ( )
Vì 2p−q +1≥ 2 ⇒ 2n−k−q ≥ 2 ⇒ 2n−k−q là số chẵn ⇒ 2p−q +1 là số chẵn
⇒ 2p−q =1⇒ p − q = 0 ⇔ p = q ⇒ x = x (đpcm). 1 2
NHÓM TOÁN TIỂU HỌC – THCS - THPT VIỆT NAM Trang 6
Sản phẩm của: “Nhóm Toán Tiểu Học-THCS-THPT VIỆT NAM” Cách 2:
Đặt = 2n; = 2m; = 2p a b c ( ; m ; n p∈). Xét phương trình 2
ax + bx + c = 0 ( ) 1 có 2 2m n+ p+2
∆ = b − 4ac = 2 − 2 . Để phương trình ( )
1 có nghiệm nguyên thì ∆ là số chính phương. 2m n+ p+2 2 ⇒ 2 − 2 = k (k ∈) n+ p+2 ⇔ 2 = (2m − )(2m k + k )
2m − k = 2u u v ⇒ (u < v) m 2 + 2 u 1 ⇒ 2 =
= 2 − (1+ 2v−u . m v ) 2 − k = 2 2
Nếu u ≠ v thì 1+ 2v−u là số lẻ và khác 1 (vô lý).
Suy ra u = v ⇒ k = 0 ⇒ ∆ = 0 . Do đó, phương trình ( )
1 có hai nghiệm bằng nhau.
____________________ HẾT ____________________
NHÓM TOÁN TIỂU HỌC – THCS - THPT VIỆT NAM Trang 7
Document Outline
- 20210625-162248_p0-converted
- CHUYEN-ĐHSP-HA-NOI-TS10- Vòng 2




