Đề tuyển sinh lớp 10 chuyên môn Toán (chuyên) năm 2022 – 2023 sở GD&ĐT Vĩnh Long

SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN VĨNH LONG NĂM HỌC 2022 – 2023 Môn: TOÁN (chuyên) ĐỀ CHÍNH THỨC Khóa thi ngày: 04/6/2022
Thời gian làm bài: 150 phút (không kể thời gian giao đề) Câu 1. (2.0 điểm)  x  3 x  2 1  1 a) Cho biểu thức P     :
với x  0 và x  4. Rút gọn biểu thức x x  8 x  2   x
P và tìm giá trị của P tại x  14  6 5 . 3  2 2 3  2 2
b) Tính giá trị biểu thức  . 17 12 2 17 12 2
Câu 2. (1.0 điểm) Cho phương trình 2
x  (m  2)x  m  3  0 ( x là ẩn số, mlà tham số).
Tìm m để phương trình có hai nghiệm phân biệt x , x sao cho biểu thức A  2x x  x  x  3 1 2  1 22 1 2
đạt giá trị lớn nhất. Câu 3. (1.5 điểm)
a) Giải phương trình x 1  2x 1  5 . x(x  3)(2x  y)  30
b) Giải hệ phương trình  . 2 x  5x  y  13 Câu 4. (1.5 điểm) a) Cho A   2023 2023 2023 2 1  2  ...  2022
. Chứng minh rằng A chia hết cho 2022.
b) Tìm các nghiệm nguyên của phương trình 2 2 2x  5y  4x  21.
Câu 5. (2.0 điểm) Cho đường tròn O đường kính AB . Gọi H là điểm thuộc đoạn thẳng
AO ( H  A, H  O ). Qua H vẽ đường thẳng vuông góc với AB , đường thẳng này cắt đường tròn
O tại C và D . Hai đường thẳng BC và AD cắt nhau tại M . Gọi N là hình chiếu của M trên đường thẳng AB . a) Chứng minh  ACN   AMN . b) Chứng minh 2 CH  NH.OH .
c) Tiếp tuyến tại A của đường tròn (O) cắt NC tại E . Chứng minh đường thẳng EB đi qua
trung điểm của đoạn thẳng CH .
Câu 6. (1.0 điểm) Cho hình vuông ABCD nội tiếp đường tròn O; R , trên dây cung DC lấy
điểm E sao cho DC  3DE , đường thẳng AE cắt cung nhỏ DC tại M . Gọi I là giao điểm của
BM và DC , vẽ OH vuông góc với DM tại H . Tính độ dài các đoạn thẳng AE và DI theo R .
Câu 7. (1.0 điểm) Cho hai số thực không âm a , b . a) Chứng minh a  b   2 2 2 a  b  . 2ab b) Biết 2 2
a  b  6. Tìm giá trị lớn nhất của biểu thức P  . a  b  2 - HẾT -
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ............................................... SBD: ..............................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN VĨNH LONG NĂM HỌC 2022 – 2023 Môn thi: TOÁN (chuyên) ĐỀ CHÍNH THỨC HƯỚNG DẪN CHẤM Câu 1. (2.0 điểm)  x  3 x  2 1  1 a) Cho biểu thức P     : 
với x  0 và x  4 . Rút gọn biểu thức P và x x 8 x 2    x  
tìm giá trị của P tại x 14  6 5 . 3  2 2 3  2 2
b) Tính giá trị biểu thức  . 17 12 2 17 12 2 Câu Điểm 1 2.0
Với x  0; x  4 , ta có:  x  3 x  2 1  1 P     :  x x 8 x 2      x 0.25   x  3 x  2 x  2 x  4        x 
x    x  x  x    . x x 2 2 4 2 2 4  x  2 x   x  0.25
x  2x  2 x  4. . x  2 x  4 2 2
Ta có x  14  6 5  9  2.3. 5  5  3 5  x  3 5  3 5  3 5. 0.25 3  5 3  5 3  5 1 Khi đó, ta có: P     0.25
14  6 5  2.3 5  4 248 5 8.3 5 . 8 3  2 2 3  2 2 1 1 b)  0.5      2   2 32 2 32 2 3 2 2 3 2 2 1 1 1 1      2 (vì 2 1  0 ) 2 1 2 1 2 1 2 1 0.5
Câu 2. (1.0 điểm) Cho phương trình 2
x  (m  2)x  m  3  0 ( x là ẩn số, mlà tham số). Tìm
m để phương trình có hai nghiệm phân biệt x , x sao cho biểu thức A  2x x  x  x  3 đạt giá 1 2  1 22 1 2 trị lớn nhất. 2 1.0
Ta có   m  2  m   m  m   m  2 2 2 4( 3) 8 16 4  0 0.25
Để phương trình có hai nghiệm phân biệt khi 2
  0  (m 4)  0  m  4 x  x  2  m
Theo định lí vi-ét ta có 1 2  0.25 x x  m  3  1 2 1
A  2x x   x  x 2  3  6x x   x  x 2  3 2  m 10m 19 0.25 1 2 1 2 1 2 1 2 2
 A  6  (m 5)  6, m  .
Dấu đẳng thức xảy ra khi m  5  0  m  5 (thỏa điều kiện m  4 ) 0.25
Vậy A đạt giá trị lớn nhất là Max A  6 khi m  5 . Câu 3. (1.5 điểm)
a) Giải phương trình x 1  2x 1  5 . x(x  3)(2x  y)  30
b) Giải hệ phương trình  . 2 x  5x  y  13 3 1.5
Ta có x 1  2x 1  5 x  1  0.25   3
 x  2  2 (x 1)(2x 1)  25  x  1  1   x  9     . 0.25 2
2 2x 3x 1  27  3x 2 2
4(2x  3x 1)  (27  3x) 1   x  9    x  5 . 0.25 2 x 150x  725  0 2
(x  3x)(2x  y)  30
b) Hệ đã cho tương đương với  2
x  3x  2x  y 13 t 10 Suy ra 2
x  3x và 2x  y là 2 nghiệm của phương trình 2 t 13t  30  0   0.25 t  3 2 x  3x 10 2 x  3x  3
Vậy hệ đã cho tương đương với  (I ) hoặc  (II ) 2x  y  3 2x  y  10 x  2  y  1 Giải (I): 2 2
x  3x  10  x  3x 10  0   x  5   y  13  3 21 x   y  13  21 Giải (II): 2 2 x  3x  3  0    3 21 x   y  13  21 0.5  2  3   21   3   21 
Vậy hệ đã cho có 4 nghiệm  ;13  21  ;  ;13  21 ;2;  1  ; 2      2    5  ;13 . Câu 4. (1.5 điểm) a) Cho A   2023 2023 2023 2 1  2  ... 2022
. Chứng minh rằng A chia hết cho 2022.
b) Tìm các nghiệm nguyên của phương trình 2 2 2x 5y  4x  21. 4 1.5
a) Với 2 số nguyên dương , a b bất kì ta có: 2023 2023 a b (a  ) b . Ta có: 2 2023 2023 2 1   2021 2022   0.25 2023 2023 2 2  2020 2022   ... 2023 2023 2 1  010 1012 2022   Và 2023 2.1011 2022 ; 2023 2022 2022 0.25 Suy ra A   2023 2023 2023 2 1  2 ... 2022 2022 0.25
b) Tìm các nghiệm nguyên của phương trình: 2 2 2x  5y  4x  21 (1) 0.25 x  y  x   x  2 2 2   2 2 5 4 21 2 1 5 4  y  Mà  x  2 2 1  0   2  y  2 2 5 4
 0  y  4  y 1;  4 0.25  x  2 + 2 y 1vào (1) tìm được 2 2x  4x 16  0   x  4  2   6 x  + 2
y  4 vào (1) tìm được 2 2 2x  4x 1  0   0.25  2   6 x   2
Vậy các nghiệm nguyên của phương trình là: 2,  1 ;2,  1 ; 4  ,  1 ; 4  ,  1 .
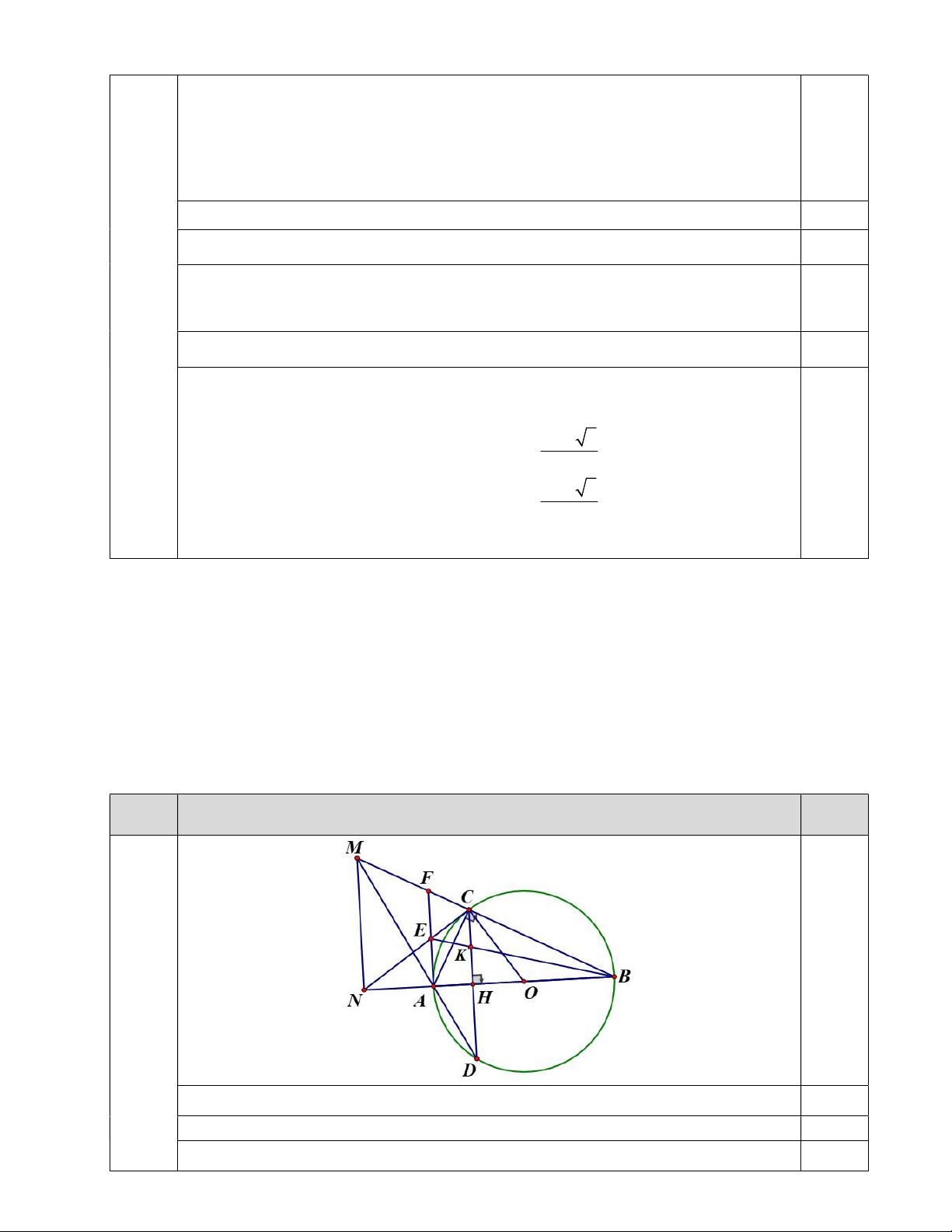
Câu 5. (2.0 điểm) Cho đường tròn O đường kính AB . Gọi H là điểm thuộc đoạn thẳng AO
( H  A, H  O ). Qua H vẽ đường thẳng vuông góc với AB , đường thẳng này cắt đường tròn O
tại C và D . Hai đường thẳng BC và AD cắt nhau tại M . Gọi N là hình chiếu của M trên đường thẳng AB . a) Chứng minh  ACN   AMN . b) Chứng minh 2 CH  NH.OH .
c) Tiếp tuyến tại A của đường tròn (O) cắt NC tại E . Chứng minh đường thẳng EB đi qua
trung điểm của đoạn thẳng CH . 5 2.0
a) Tứ giác MNAC có     90o  90o 180o MNA MCA 0.25
nên MNAC là tứ giác nội tiếp. 0.25   ACN   AMN . 0.25 3 b) Ta có:  ACN   AMN  AMN  
ADC (do MN//DC vì cùng vuông góc với AB) 0.25
AB  CD suy ra H là trung điểm của CD .
Tam giác ACD là tam giác cân do AH vừa là đường cao, vừa là trung tuyến. 0.25 Suy ra  ADC   ACD . Từ đó ta có:  ACN   ACD .
Ta có:         9  0O NCO ACN ACO ACD OAC . Suy ra CN  CO . 0.25  NCO vuông tại C 2  CH  NH.OH . 1 c)  ACE   EAC (cùng bằng sd 
AC ).  AEC cân tại E  E thuộc đường trung 2
trực của AC . Gọi F  AE  BM 0.25
Ta có C thuộc đường tròn đường kính FA . Nên đường trung trực của AC phải cắt
đường kính FA tại tâm của đường tròn này. Suy ra E là trung điểm của FA . CK KH  BK 
Gọi K  CH  BE . Ta có: CH / /FA nên     . FE EA  BE  0.25
Mà FE  EA nên CK  KH . Vậy BE đi qua trung điểm của CH .
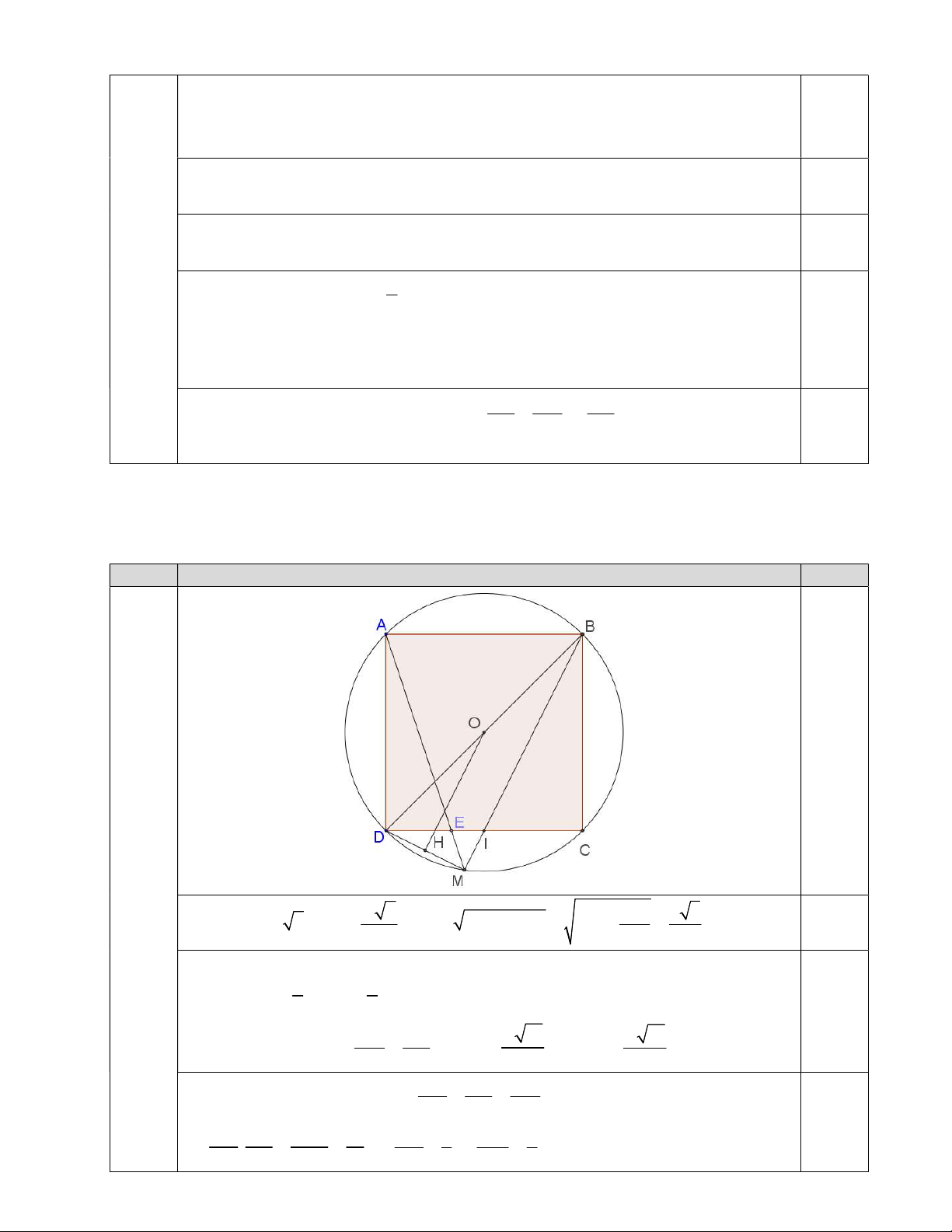
Câu 6. (1.0 điểm) Cho hình vuông ABCD nội tiếp đường tròn  ;
O R , trên dây cung DC lấy
điểm E sao cho DC  3DE , đường thẳng AE cắt cung nhỏ DC tại M . Gọi I là giao điểm của
BM và DC , vẽ OH vuông góc với DM tại H . Tính độ dài các đoạn thẳng AE và DI theo R . 6 1.0 R 2 2 2R 2 5 Ta có AD  R 2 ; DE  ; 2 2 2 AE  AD  DE  2R   R . 0.25 3 9 3
Tam giác DOM cân tại O mà OH  DM 1 1 Suy ra  DOH   DOM  sd  DM   DAM 2 2 0.25 DH DE   10 R 10 OHD ∽ A  DE     R DH  DM  OD AE 10 5 ME DE MD
Ta có DEM ∽ AEC (g-g)    CE AE AC 0.25 2 ME DE MD 1  ME 1 ME 1 .       2 AE CE AC 10 AE 5 AM 6 4 EI ME 1 1 R 2 EI //AB     EI  AB  AB AM 6 6 6 0.25 R 2 R 2 R 2  DI  DE  EI    . 3 6 2
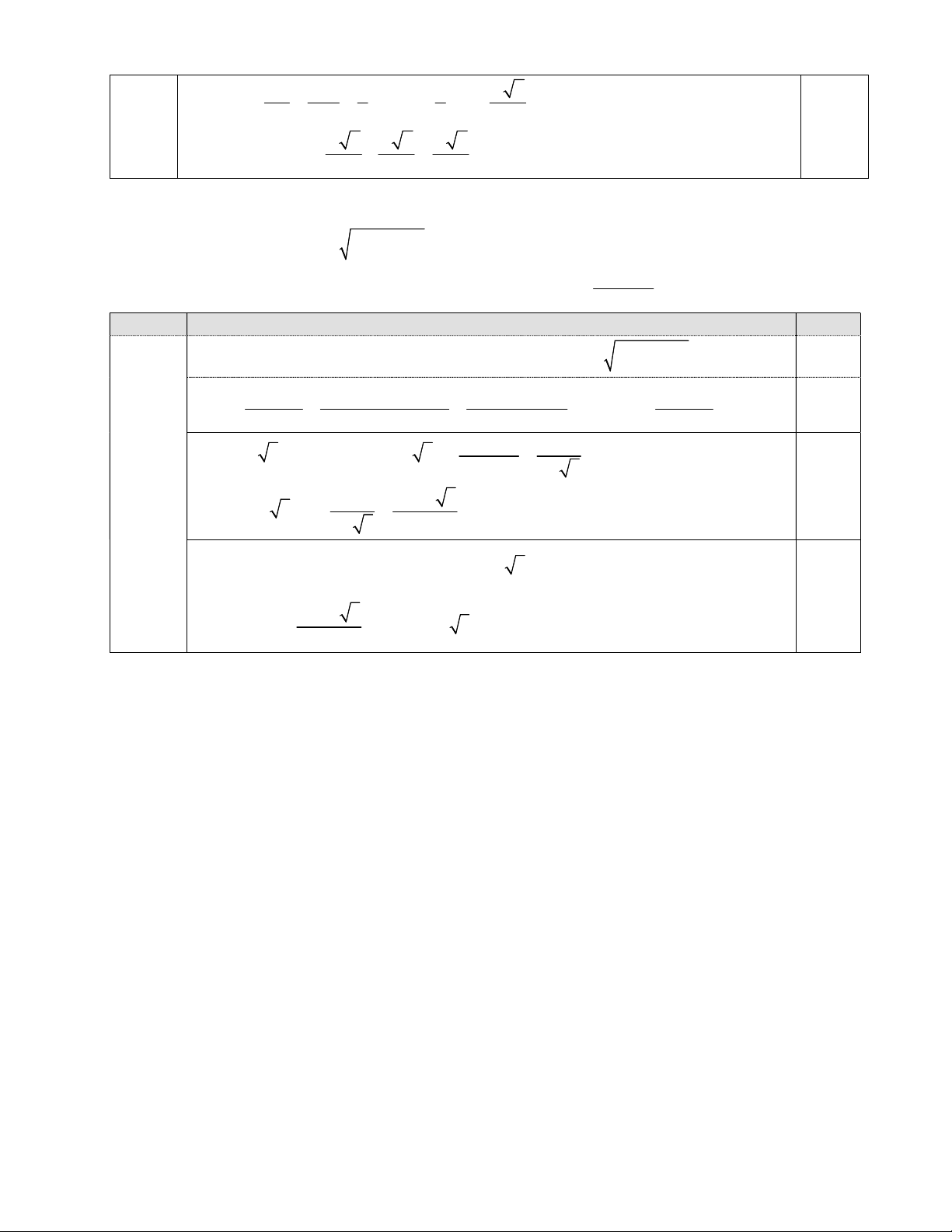
Câu 7. (1.0 điểm) Cho hai số thực không âm a , b . a) Chứng minh a  b   2 2 2 a  b  . 2ab b) Biết 2 2
a  b  6 . Tìm giá trị lớn nhất của biểu thức P  . a  b  2 7 1.0
a) Ta có: ab  a  b  a  b2 2 2   2 2 a  b   a  b   2 2 2 2 2 a  b  . 0.25 2ab a b2  2 2
a  b  a  b2  4  2 2 b) P     a  b  2  0.25 a  b  2 a  b  2 a  b  2 a  b  2 2 1
a  b  2 3  a  b  2  2  2 3   a  b  2 1 3 0.25 1 3   3 3 Vậy P  2 3  2   . 1 3 2 2 2 a  b  6
Dấu “” xảy ra khi   a  b  3 . a  b 0.25 3   3 3 Vậy M x a P  khi a  b  3 . 2 - HẾT - 5