Đề tuyển sinh lớp 10 chuyên môn Toán (chuyên) năm 2023 – 2024 sở GD&ĐT Hà Nam

Giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi tuyển sinh vào lớp 10 THPT chuyên môn Toán (đề chuyên) năm học 2023 – 2024 sở Giáo dục và Đào tạo UBND tỉnh Hà Nam; kỳ thi được diễn ra vào thứ Ba ngày 30 tháng 05 năm 2023. Mời bạn đọc đón xem!

44 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

7 trang 8 tháng trước

Tác giả:

Profile Vũ Hường
Câu I. (2,0 điểm)
Cho biểu thức
11 2
1
12
xx x x
A
x
xx xx

−+−
= −

−
++ − −

với
0, 1, 4.
x xx≥ ≠≠
1. Rút gọn biểu thức
.A
2. Tìm tất cả các số nguyên của
x
để
2 1 1 2.AA−+=
Câu II. (2,0 điểm)
1. Giải phương trình
22
( 1) 6 16 2 6 4.x xx xx− ++= −+
2. Giải hệ phương trình
3 23
22 2
2 (2 ) 2 6 3
.
3( ) 7 5 5 14 4
x xy y x x x xy y y
x y x y yx
+ −+ + = ++
+ ++ + + =−−
Câu III. (1,0 điểm)
Tìm tất cả các số tự nhiên
n
để
là số chính phương.
Câu IV. (4,0 điểm)
Cho đường tròn
(
)
O
có dây cung
BC
cố định và không đi qua tâm
O
. Gọi
A
là
điểm di động trên đường tròn
( )
O
sao cho tam giác
ABC
nhọn và
.AB AC<
Gọi
M
là
trung điểm của cạnh
BC
và
H
là trực tâm tam giác
.
ABC
Tia
MH
cắt đường tròn
(
)
O
tại
K
, đường thẳng
AH
cắt cạnh
BC
tại
D
và
AE
là đường kính của đường tròn
( )
O
.
1. Chứng minh
.BAD CAE=
2. Chứng minh rằng tứ giác
BHCE
là hình bình hành và
..HA HD HK HM=
.
3. Tia
KD
cắt đường tròn
(
)
O
tại
I
(
I
khác
K
), đường thẳng đi qua
I
và vuông
góc với đường thẳng
BC
cắt
AM
tại
J
. Chứng minh rằng các đường thẳng
,AK BC
và
HJ
cùng đi qua một điểm.
4. Một đường tròn thay đổi luôn tiếp xúc với
AK
tại
A
và cắt các cạnh
,AB AC
lần lượt tại
,PQ
phân biệt. Gọi
N
là trung điểm của đoạn thẳng
PQ
. Chứng minh rằng
đường thẳng
AN
luôn đi qua một điểm cố định.
Câu V. (1,0 điểm) Cho
,,abc
là ba số thực dương thỏa mãn điều kiện
222
111
1++=
abc
.
Tìm giá trị lớn nhất của biểu thức:
2 22 22 2
111
522 522 522
= ++
++ ++ ++
P
a ab b b bc c c ca a
.
--- HẾT---
Thí sinh được sử dụng máy tính bỏ túi không có chức năng soạn thảo văn bản và không
có thẻ nhớ.
Họ và tên thí sinh:………………………...Số báo danh:.................................................
Cán bộ coi thi số 1……………………… Cán bộ coi thi số 2…………….........................
UBND TỈNH HÀ NAM
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ CHÍNH THỨC
(Đề thi gồm 01 trang)
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
NĂM HỌC 2023 - 2024
Môn: TOÁN (Đề chuyên)
Thời gian làm bài: 150 phút, không kể thời gian giao đề
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NAM
ĐỀ CHÍNH THỨC
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
Năm học: 2023-2024
(Hướng dẫn chấm thi có 06 trang)
HƯỚNG DẪN CHẤM MÔN TOÁN (ĐỀ CHUYÊN)
Ghi chú:
- Điểm toàn bài không làm tròn.
- Các cách giải khác mà đúng cho điểm tương đương.
Nội dung
Điểm
Câu I (2,0 điểm) .
Cho biểu thức
11 2
1
12
xx x x
A
x
xx xx

−+−
= −

−
++ − −

với
0, 1, 4.x xx≥≠≠
1.(1,5 điểm) Rút gọn biểu thức
.A
( )
( )( ) ( )( )
3
1
12
.
1
11 12
x
xx
A
xx
xx xx

−
+−

= −

++
+− +−

0,5
( )
( ) ( )
( )
( 1)( 1) 1 2
.
1
11 12
x xx x x
xx
xx xx

− ++ + −

= −

++
+− +−

0,25
(
)
11
1
11
x
xx

=−−

−+

0,25
( )
( )
( )
2
1
11
x
xx
= −
−+
0,25
2
.
1x
=
+
0,25
2.(0,5 điểm) Tìm tất cả các số nguyên của
x
để
2 1 1 2.AA−+=
+)
1
2112 2121210
2
A AA A A A−+= ⇔ − = −⇔ −≥ ⇔ ≥
0,25
+)
21
39
2
1
xx
x
≥ ⇔ ≤⇔≤
+
Kết hợp với điều kiện
{ }
0; 1; 4 0; 2;3;5;6;7;8;9x xx x≥ ≠ ≠⇒∈
0,25
Câu II (2,0 điểm).
1.(1,0 điểm) Giải phương trình
22
( 1) 6 16 2 6 4.x xx xx− ++= −+
22 2
( 1) 6 16 2 6 4 ( 1) 6 16 ( 1)(2 4)x xx xx x xx x x− ++= −+⇔− ++=− −
2
( 1)( 6 16 2 4) 0x xx x⇔− ++−+=
0,25
+)
10 1xx−= ⇔ =
0,25
+)
2
22
2 40
6 16 2 4
6 16 (2 4)
x
xx x
xx x
−≥
+ + = −⇔
++= −
2
2
2
2
0( )
3 22 0
22
()
3
x
x
xl
xx
x tm
≥
≥
=
⇔⇔

−=
=
0,25
Phương trình đã cho có hai nghiệm
22
1;
3
xx= =
0,25
2.(1,0 điểm) Giải hệ phương trình
3 23
22 2
2 (2 ) 2 6 3 (1)
.
3( ) 7 5 5 14 4 (2)
x xy y x x x xy y y
x y x y yx
+ −+ + = ++
+ ++ + + =−−
Điều kiện:
2
2
3( ) 7 0
5 5 14 0
xy
xy
+ +≥
++≥
Phương trình
(1)
tương đương với
3 22 2 3
32 23 2
22
22
22 26 3
(2 ) (2 ) (2 ) (6 3 ) 0
(2 ) (2 ) (2 ) 3(2 ) 0
(2 )( 3) 0
x xy x y x x xy y y
x x y xy y x xy x y
x xy y xy xxy xy
x yx y x
+ − + +=++
⇔ − + −+ −+−=
⇔ −+ −+ −+ −=
⇔ − + ++ =
0,25
22
1 11
(2 )[( ) ] 0
24
xyx y⇔ − + ++ =
202
xy y x
⇔ −=⇔=
0,25
Thay
2
yx
=
vào phương trình
(2)
ta được
22 2
2 22
22
2
22
2
22
3 6 7 5 10 14 4 2
( 3 6 7 2) ( 5 10 14 3) ( 2 1) 0
3( 1) 5( 1)
( 1) 0
3 6 7 2 5 10 14 3
35
( 1) ( 1) 0
3 6 7 2 5 10 14 3
x x x x xx
xx x x xx
xx
x
xx x x
x
xx x x
+++ + +=−−
⇔ + +− + + + − + + +=
++
⇔ + ++ =
+ ++ + + +
⇔ + + +=
+ ++ + + +
0,25
Vì
22
35
10
3 6 7 2 5 10 14 3xx x x
+ +>
+ ++ + + +
nên phương trình tương đương với
2
( 1) 0 1 0 1 2 ( )x x x y tm+ = ⇔ += ⇔ =−⇒ =−
Vậy hệ phương trình có nghiệm
( ; ) ( 1; 2)xy =−−
0,25
Câu III. (1,0 điểm) Tìm tất cả các số tự nhiên
n
để
2024 2027
222
n
++
là số chính phương.
Giả sử số tự nhiên
n
thỏa mãn đề bài. Khi đó tồn tại số nguyên dương
k
sao cho
(
)( )
2024 2027 2 2024 2 1012 1012
2 2 2 9.2 2 3.2 3.2 2
nn n
k kk k+ +=⇔ +=⇔+ − =
.
0,25
1012
1012
3.2 2
3.2 2
,,
a
b
k
k
ab a b n
+=
⇒− =
∈ +=
1013
2 2 3.2
ab
⇒−=
.
0,25
3
1013
1013
2 13
2 (2 1) 3.2
22
ab
b ab
b
−
−
−=
⇔ −= ⇔
=
0,25
2 1015
2028
1013 1013
ab a
n
bb
−= =

⇔ ⇔ ⇒=

= =

Vậy với
2028
n
=
thì
2024 2027
222
n
++
là số chính phương
0,25
Câu IV.
(4 điểm) Cho đường tròn
(
)
O
có dây cung
BC
cố định và không đi qua tâm
O
. Gọi
A
là
điểm di động trên đường tròn
( )
O
sao cho tam giác
ABC
nhọn và
.AB AC<
Gọi
M
là trung điểm của
cạnh
BC
và
H
là trực tâm tam giác
.ABC
Tia
MH
cắt đường tròn
( )
O
tại
K
, đường thẳng
AH
cắt
cạnh
BC
tại
D
và
AE
là đường kính của đường tròn
( )
O
.
1. ( 1,0 điểm) Chứng minh
.BAD CAE=
0
90
AH BC ADB⊥⇒ =
0
90ABE
=
( góc nội tiếp chắn nửa đường tròn)
0,25
Suy ra
BAD CBE=
( cùng phụ với
ABC
)
0,25
Mà
CBE CAE=
( góc nội tiếp cùng chắn cung
AC
)
0,25
Suy ra
.BAD CAE
=
0,25
2. ( 1,0 điểm) Chứng minh rằng tứ giác
BHCE
là hình bình hành và
..HA HD HK HM=
.
H
E
K
M
D
O
B
C
A
4
Ta có
90
ACE = °
(góc nội tiếp chắn nửa đường tròn)
EC AC⇒⊥
.
Mà
H
là trực tâm tam giác
ABC
BH AC
⇒⊥
. Từ đó suy ra
//EC BH
.
Tương tự
//HC BE
0,25
Xét tứ giác
BHCE
có
//
EC BH
và
//
HC BE
nên tứ giác
BHCE
là hình bình hành.
0,25
Mà
M
là trung điểm của
BC
nên ba điểm
, , HME
thẳng hàng.
Lại có ba điểm
, , MKH
thẳng hàng. Từ đó suy ra ba điểm
,,
KHE
thẳng hàng.
Ta có
90AKE = °
(góc nội tiếp chắn nửa đường tròn)
90AKM⇒=°
.
Xét
AKH∆
và
MDH∆
có:
( )
90AKM MDH= = °
;
KHA DHM=
(hai góc đối đỉnh).
0,25
( )
.
HA HK
AKH MDH g g
HM HD
⇒∆ ∆ ⇒ =∽
..HA HD HK HM⇒=
.
0,25
3. ( 1,0 điểm) Tia
KD
cắt đường tròn
( )
O
tại
I
(
I
khác
K
), đường thẳng đi qua
I
và vuông góc với
đường thẳng
BC
cắt
AM
tại
J
. Chứng minh rằng các đường thẳng
,AK BC
và
HJ
cùng đi qua
một điểm.
Kéo dài
AK
cắt đường thẳng
BC
tại
S
,
SAM∆
có hai đường cao
AD
và
MK
cắt
nhau tại
H
H⇒
là trực tâm tam giác
SAM
.
H
E
K
M
D
O
B
C
A
5
Xét tam giác
HDM∆
và
SDA∆
có
90ADS HDM= = °
và
DMH DAS=
(cùng phụ với
ASM
).
( )
.HDM SDA g g⇒∆ ∆∽
HD DS
DM AD
⇒=
. (1)
Tương tự
H
là trực tâm
ABC∆
BD AD
BDH ADC
HD CD
⇒∆ ∆ ⇒ =∽
. (2)
0,25
Từ (1) và (2)
. . ..
HD BD DS AD BD DS
BD CD DM DS
DM HD AD CD DM CD
⇒ = ⇒=⇒ =
(3)
Mà
( )
.
BDK IDC g g∆∆∽
..
BD DK
BD CD DI DK
ID DC
⇒= ⇒ =
(4)
0,25
Từ (3) và (4)
..
DI DK DM DS
⇒=
nên
SKMI
là tứ giác nội tiếp
SMI SKI⇒=
.
Mà
AKDM
là tứ giác nội tiếp (do
90AKM ADM= = °
)
SKI DMA⇒=
.
Từ đó suy ra
SMI DMA=
.
Xét
MIJ∆
có
SMI DMA=
và
IJ BC
⊥
BC
⇒
là đường trung trực của
IJ
.
0,25
90SJM SIM⇒==°
(vì
SKMI
là tứ giác nội tiếp nên
180SIM SKM
= °−
180 90 90= °− °= °
)
SJ AM⇒⊥
.
Mà
H
là trực tâm
SAM∆
SH AM⇒⊥
. Từ đó suy ra ba điểm
,,
SHJ
thẳng hàng. Vậy
các đường thẳng
,AK BC
và
HJ
cùng đi qua điểm
S
.
0,25
4.(1,0 điểm) Một đường tròn thay đổi luôn tiếp xúc với
AK
tại
A
và cắt các cạnh
,
AB AC
lần
lượt tại
,
PQ
phân biệt. Gọi
N
là trung điểm của đoạn thẳng
PQ
. Chứng minh rằng đường
thẳng
AN
luôn đi qua một điểm cố định.
Gọi
'N
là giao điểm của
PQ
và
.AE
Xét
'AQN∆
và
BEM∆
có:
'QAN EBM=
;
'
AQN KAP BEM= =
( )
'
'.
'
AN BM
AQN BEM g g
QN EM
⇒∆ ∆ ⇒ =∽
(5)
0,25
Do
'QAN EBM=
;
'AQN KAP BEM= =
nên theo tính chất góc ngoài của
'AQN∆
và
BEM∆
ta có
'EMC PN A=
.
0,25
N
≡
N'
H
P
Q
E
K
M
D
O
B
C
A
O'
6
Mà
'PAN ECM=
nên
( )
'.ECM PAN g g∆∆∽
'
'
CM AN
EM PN
⇒=
. (6)
0,25
Từ (5) và (6) và kết hợp
BM CM=
''
'' '
''
AN AN
QN PN N N
QN PN
⇒ = ⇒ = ⇒≡
.
Vậy
AN
luôn đi qua một điểm cố định
O
.
0,25
Câu V. (1,0 điểm)Cho
,,abc
là ba số thực dương thỏa mãn điều kiện
222
111
1++=
abc
.
Tìm giá trị lớn nhất của biểu thức:
2 22 22 2
111
522 522 522
= ++
++ ++ ++
P
a ab b b bc c c ca a
.
Với
,, 0abc>
, chứng minh được:
( )
( )
2
2 22
222
111 1 1111
9
9
111 1 1 1
3( ) 3
abc
abc abc abc
xyz x y z
abc a b c
 
++ ++ ≥⇒ ≤ ++
 
++
 

++ ≤ + + ⇒ ++≤ + +


0,25
Với
,0ab>
, ta có :
2 2 2 22 2
22 2
22 2
522(44)(2)
(2 ) ( ) (2 )
522 (2)2
a ab b a ab b a ab b
ab ab ab
a ab b ab ab
++= +++−+
= + +− ≥ +
⇒ + + ≥ +=+
0,25
22
1 1 11 1 1 12 1
29 9
522
ab aab ab
a ab b

⇒ ≤ ≤ ++ = +

+

++
Tương tự:
22 22
1 12 1 1 12 1
;
99
522 522
bc ca
b bc c c ca a

≤+ ≤+


++ ++
0,25
222
1212121 1111 1 1 1 1 1 3
33
9 3 3 33
PP
abbcca abc a b c

≤ +++++ = ++ ⇒≤⋅ + + =⋅ =


Dấu “=” xảy ra
222
3
111
1
abc
abc
abc
= =
⇔ ⇔===
++=
Vậy
3
max
3
P =
khi
3abc= = =
.
0,25
--HẾT--
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

UBND TỈNH HÀ NAM
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024
Môn: TOÁN (Đề chuyên) ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian giao đề
(Đề thi gồm 01 trang)
Câu I. (2,0 điểm)  −  + −  Cho biểu thức x x 1 x 1 x 2 A =   −
 với x ≥ 0, x ≠ 1, x ≠ 4. 1+ x + x x −1 x − x −   2  1. Rút gọn biểu thức . A
2. Tìm tất cả các số nguyên của x để 2A −1 +1 = 2 . A
Câu II. (2,0 điểm) 1. Giải phương trình 2 2
(x −1) x + 6x +16 = 2x − 6x + 4. 3 2 3
2x + xy(2y − x) + 2x + 6x = xy + y +  3y
2. Giải hệ phương trình  . 2 2 2
 3(x + y) + 7 + 5x + 5y +14 = 4 − y − x
Câu III. (1,0 điểm)
Tìm tất cả các số tự nhiên n để 2024 2027 2 2 2n + + là số chính phương.
Câu IV. (4,0 điểm)
Cho đường tròn (O) có dây cung BC cố định và không đi qua tâm O . Gọi A là
điểm di động trên đường tròn (O) sao cho tam giác ABC nhọn và AB < AC. Gọi M là
trung điểm của cạnh BC và H là trực tâm tam giác ABC. Tia MH cắt đường tròn (O)
tại K , đường thẳng AH cắt cạnh BC tại D và AE là đường kính của đường tròn (O) . 1. Chứng minh  =  BAD CAE.
2. Chứng minh rằng tứ giác BHCE là hình bình hành và .
HA HD = HK.HM .
3. Tia KD cắt đường tròn (O) tại I ( I khác K ), đường thẳng đi qua I và vuông
góc với đường thẳng BC cắt AM tại J . Chứng minh rằng các đường thẳng AK, BC và
HJ cùng đi qua một điểm.
4. Một đường tròn thay đổi luôn tiếp xúc với AK tại A và cắt các cạnh AB, AC
lần lượt tại P, Q phân biệt. Gọi N là trung điểm của đoạn thẳng PQ . Chứng minh rằng
đường thẳng AN luôn đi qua một điểm cố định.
Câu V. (1,0 điểm) Cho a,b,c là ba số thực dương thỏa mãn điều kiện 1 1 1 + + = 1. 2 2 2 a b c
Tìm giá trị lớn nhất của biểu thức: 1 1 1 P = + + . 2 2 2 2 2 2
5a + 2ab + 2b
5b + 2bc + 2c
5c + 2ca + 2a --- HẾT---
Thí sinh được sử dụng máy tính bỏ túi không có chức năng soạn thảo văn bản và không có thẻ nhớ.
Họ và tên thí sinh:………………………...Số báo danh:.................................................
Cán bộ coi thi số 1……………………… Cán bộ coi thi số 2…………….........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN HÀ NAM Năm học: 2023-2024
(Hướng dẫn chấm thi có 06 trang) ĐỀ CHÍNH TH ỨC
HƯỚNG DẪN CHẤM MÔN TOÁN (ĐỀ CHUYÊN) Ghi chú:
- Điểm toàn bài không làm tròn.
- Các cách giải khác mà đúng cho điểm tương đương. Nội dung Điểm
Câu I (2,0 điểm) .  −  + −  Cho biểu thức x x 1 x 1 x 2 A =   −
 với x ≥ 0, x ≠ 1, x ≠ 4. 1+ x + x x −1 x − x −   2 
1.(1,5 điểm) Rút gọn biểu thức . A ( x)3 −1  x +1 x − 2  A = . −  0,5
1+ x + x ( x + )1( x − )1 ( x + )1( x −2) ( x 1)(x x 1)  x +1 x − 2  − + + = . −  0,25 1+ x + x  ( x + )
1 ( x − )1 ( x + )1( x − 2) ( x ) 1 1 1  = − −   0,25 x −1 x +1 = ( x − ) 2 1 ( x − ) 1 ( x + ) 1 0,25 2 = . 0,25 x +1
2.(0,5 điểm) Tìm tất cả các số nguyên của x để 2A −1 +1 = 2 . A +) 1
2A −1 +1 = 2A ⇔ 2A −1 = 2A −1 ⇔ 2A −1≥ 0 ⇔ A ≥ 0,25 2 2 1 +)
≥ ⇔ x ≤ 3 ⇔ x ≤ 9 x +1 2
Kết hợp với điều kiện x ≥ 0; x ≠ 1; x ≠ 4 ⇒ x ∈{0;2;3;5;6;7;8; } 9 0,25
Câu II (2,0 điểm).
1.(1,0 điểm) Giải phương trình 2 2
(x −1) x + 6x +16 = 2x − 6x + 4. 2 2 2
(x −1) x + 6x +16 = 2x − 6x + 4 ⇔ (x −1) x + 6x +16 = (x −1)(2x − 4) 2
⇔ (x −1)( x + 6x +16 − 2x + 4) = 0 0,25
+) x −1 = 0 ⇔ x = 1 0,25 2x − 4 ≥ 0 +) 2
x + 6x +16 = 2x − 4 ⇔  2 2
x + 6x +16 = (2x − 4) 2 x ≥ 2 x 2  ≥  = x 0(l) ⇔  ⇔ 2  3  x 22x 0  − =  22  0,25 x = (tm)  3 22
Phương trình đã cho có hai nghiệm x = 1; x = 0,25 3 3 2 3
2x + xy(2y − x) + 2x + 6x = xy + y +  3y (1)
2.(1,0 điểm) Giải hệ phương trình  . 2 2 2
 3(x + y) + 7 + 5x + 5y +14 = 4 − y − x (2) 2 3(
 x + y) + 7 ≥ 0 Điều kiện:  2 5
 x + 5y +14 ≥ 0
Phương trình (1) tương đương với 3 2 2 2 3
2x + 2xy − x y + 2x + 6x = xy + y + 3y 3 2 2 3 2
⇔ (2x − x y) + (2xy − y ) + (2x − xy) + (6x − 3y) = 0 2 2
⇔ x (2x − y) + y (2x − y) + x(2x − y) + 3(2x − y) = 0 2 2
⇔ (2x − y)(x + y + x + 3) = 0 0,25 1 2 2 11
⇔ (2x − y)[(x + ) + y + ] = 0 2 4
⇔ 2x − y = 0 ⇔ y = 2x 0,25
Thay y = 2x vào phương trình (2) ta được 2 2 2
3x + 6x + 7 + 5x +10x +14 = 4 − 2x − x 2 2 2
⇔ ( 3x + 6x + 7 − 2) + ( 5x +10x +14 − 3) + (x + 2x +1) = 0 2 2 3(x +1) 5(x +1) 2 ⇔ + + (x +1) = 0 2 2 3x + 6x + 7 + 2 5x +10x +14 + 3 2 3 5 ⇔ (x +1) ( + +1) = 0 2 2 3x + 6x + 7 + 2 5x +10x +14 + 3 0,25 3 5 Vì +
+1 > 0 nên phương trình tương đương với 2 2 3x + 6x + 7 + 2 5x +10x +14 + 3 2
(x +1) = 0 ⇔ x +1 = 0 ⇔ x = 1 − ⇒ y = 2 − (tm)
Vậy hệ phương trình có nghiệm ( ; x y) = ( 1; − 2 − ) 0,25
Câu III. (1,0 điểm) Tìm tất cả các số tự nhiên n để 2024 2027 2 2 2n +
+ là số chính phương.
Giả sử số tự nhiên n thỏa mãn đề bài. Khi đó tồn tại số nguyên dương k sao cho 2024 2027 n 2 2024 n 2 + + = ⇔ + = ⇔ ( 1012 + )( 1012 2 2 2 9.2 2 3.2 − 3.2 ) = 2n k k k k . 0,25 1012 k + 3.2 = 2a  1012 ⇒ k −3.2 = 2b a b 1013 ⇒ 2 − 2 = 3.2 . 0,25
a,b∈ ,a +b = n   3  − = − 2a−b 1 3 b a b 1013 ⇔ 2 (2 −1) = 3.2 ⇔  b 1013  0,25 2 = 2 a − b = 2 a = 1015 ⇔  ⇔  ⇒ n = 2028 b  = 1013 b  = 1013
Vậy với n = 2028thì 2024 2027 2 2 2n + + là số chính phương 0,25
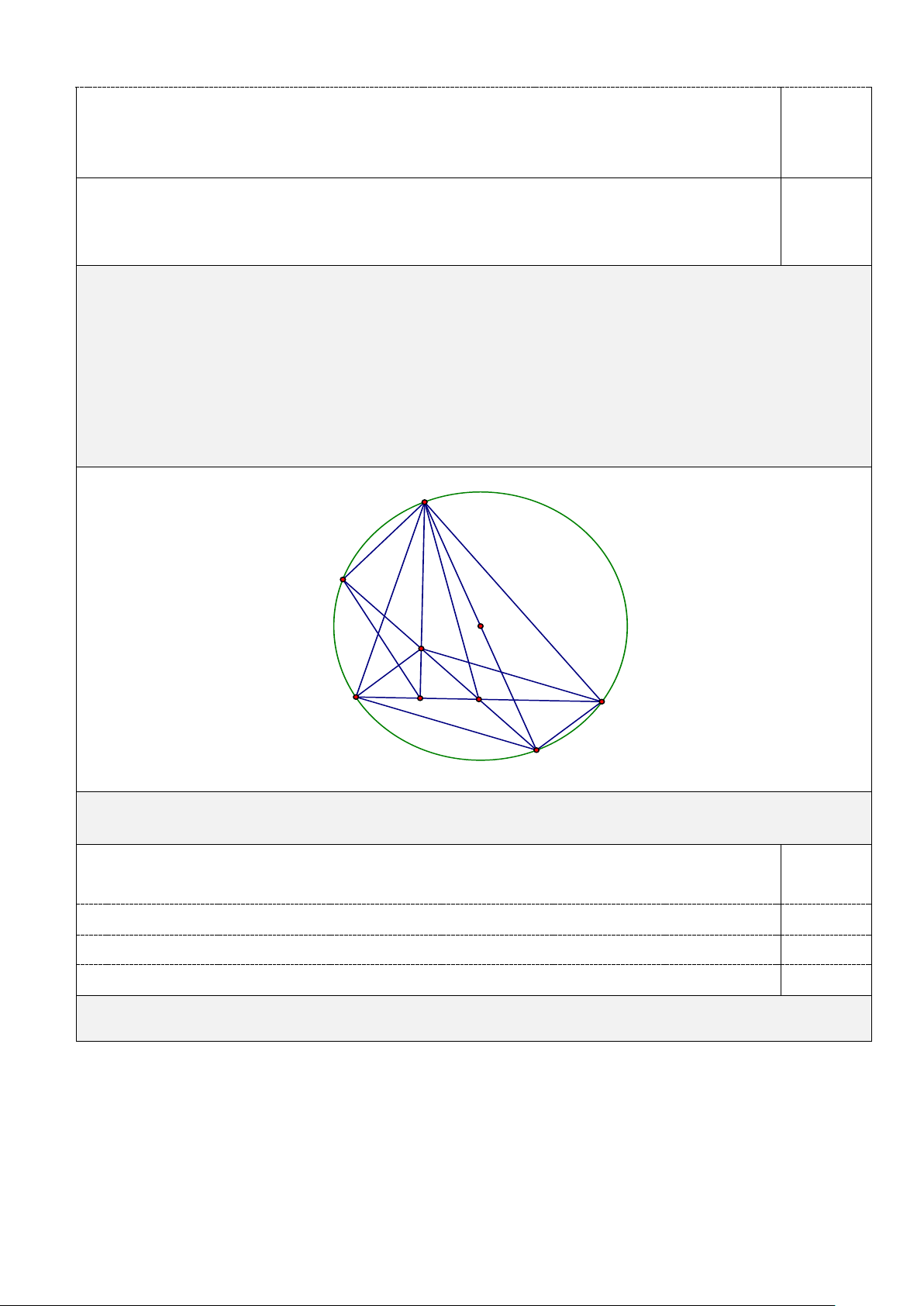
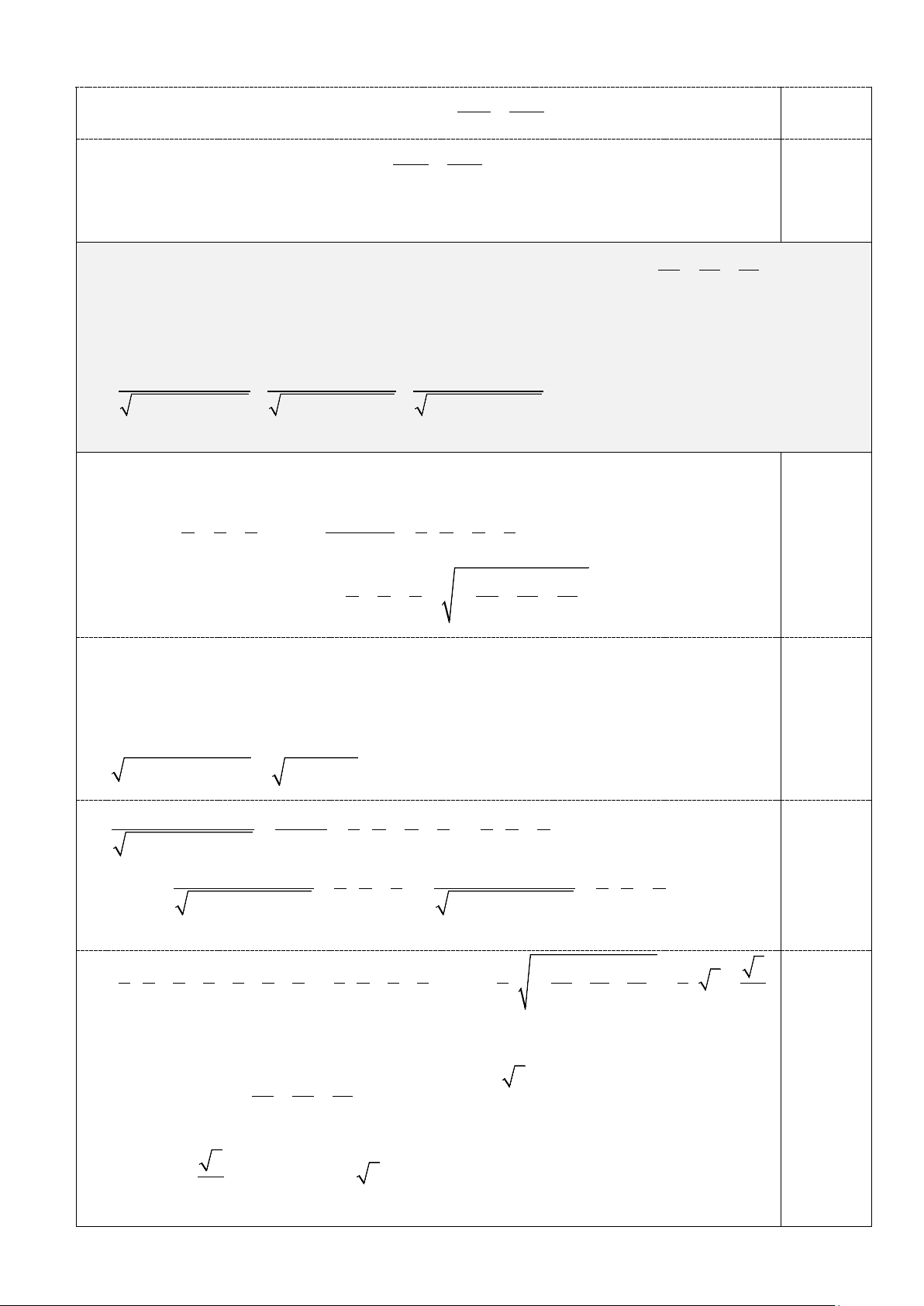
Câu IV. (4 điểm) Cho đường tròn (O) có dây cung BC cố định và không đi qua tâm O . Gọi A là
điểm di động trên đường tròn (O) sao cho tam giác ABC nhọn và AB < AC. Gọi M là trung điểm của
cạnh BC và H là trực tâm tam giác ABC. Tia MH cắt đường tròn (O) tại K , đường thẳng AH cắt
cạnh BC tại D và AE là đường kính của đường tròn (O) . A K O H D B M C E
1. ( 1,0 điểm) Chứng minh  =  BAD CAE. ⊥ ⇒  0 AH BC ADB = 90  0
ABE = 90 ( góc nội tiếp chắn nửa đường tròn) 0,25 Suy ra  = 
BAD CBE ( cùng phụ với  ABC ) 0,25 Mà  = 
CBE CAE ( góc nội tiếp cùng chắn cung  AC ) 0,25 Suy ra  =  BAD CAE. 0,25
2. ( 1,0 điểm) Chứng minh rằng tứ giác BHCE là hình bình hành và .
HA HD = HK.HM . 4 A K O H D B M C E Ta có 
ACE = 90° (góc nội tiếp chắn nửa đường tròn) ⇒ EC ⊥ AC .
Mà H là trực tâm tam giác ABC ⇒ BH ⊥ AC . Từ đó suy ra EC // BH .
Tương tự HC // BE 0,25
Xét tứ giác BHCE có EC // BH và HC // BE nên tứ giác BHCE là hình bình hành. 0,25
Mà M là trung điểm của BC nên ba điểm H, M , E thẳng hàng.
Lại có ba điểm M , K, H thẳng hàng. Từ đó suy ra ba điểm K, H, E thẳng hàng. Ta có 
AKE = 90° (góc nội tiếp chắn nửa đường tròn) ⇒  AKM = 90° . Xét A ∆ KH và MD ∆ H có:  = 
AKM MDH (= 90°) ;  = 
KHA DHM (hai góc đối đỉnh). 0,25 ⇒ ∆ ∽ ∆ ( . ) HA HK AKH MDH g g ⇒ = ⇒ .
HA HD = HK.HM . 0,25 HM HD
3. ( 1,0 điểm) Tia KD cắt đường tròn (O) tại I ( I khác K ), đường thẳng đi qua I và vuông góc với
đường thẳng BC cắt AM tại J . Chứng minh rằng các đường thẳng AK, BC và HJ cùng đi qua một điểm.
Kéo dài AK cắt đường thẳng BC tại S , S
∆ AM có hai đường cao AD và MK cắt
nhau tại H ⇒ H là trực tâm tam giác SAM . 5 Xét tam giác HDM ∆ và S ∆ DA có  = 
ADS HDM = 90° và  = 
DMH DAS (cùng phụ với ASM ). ⇒ HDM ∆ HD DS ∽ S
∆ DA (g.g) ⇒ = . (1) DM AD
Tương tự H là trực tâm A ∆ BC BD AD ⇒ B ∆ DH 0,25 ∽ A ∆ DC ⇒ = . (2) HD CD Từ (1) và (2) HD ⇒ . BD DS = . AD BD DS ⇒ = ⇒ B .
D CD = DM.DS (3) DM HD AD CD DM CD Mà B ∆ DK BD DK ∽ I
∆ DC (g.g) ⇒ = ⇒ B .
D CD = DI.DK (4) 0,25 ID DC
Từ (3) và (4)⇒ DI.DK = DM.DS nên SKMI là tứ giác nội tiếp ⇒  =  SMI SKI .
Mà AKDM là tứ giác nội tiếp (do  = 
AKM ADM = 90°) ⇒  =  SKI DMA . Từ đó suy ra  =  SMI DMA. Xét MIJ ∆ có  = 
SMI DMA và IJ ⊥ BC ⇒ BC là đường trung trực của IJ . 0,25 ⇒  = 
SJM SIM = 90° (vì SKMI là tứ giác nội tiếp nên  = ° −  SIM 180 SKM
= 180° − 90° = 90° ) ⇒ SJ ⊥ AM .
Mà H là trực tâm S
∆ AM ⇒ SH ⊥ AM . Từ đó suy ra ba điểm S, H, J thẳng hàng. Vậy
các đường thẳng AK, BC và HJ cùng đi qua điểm S . 0,25
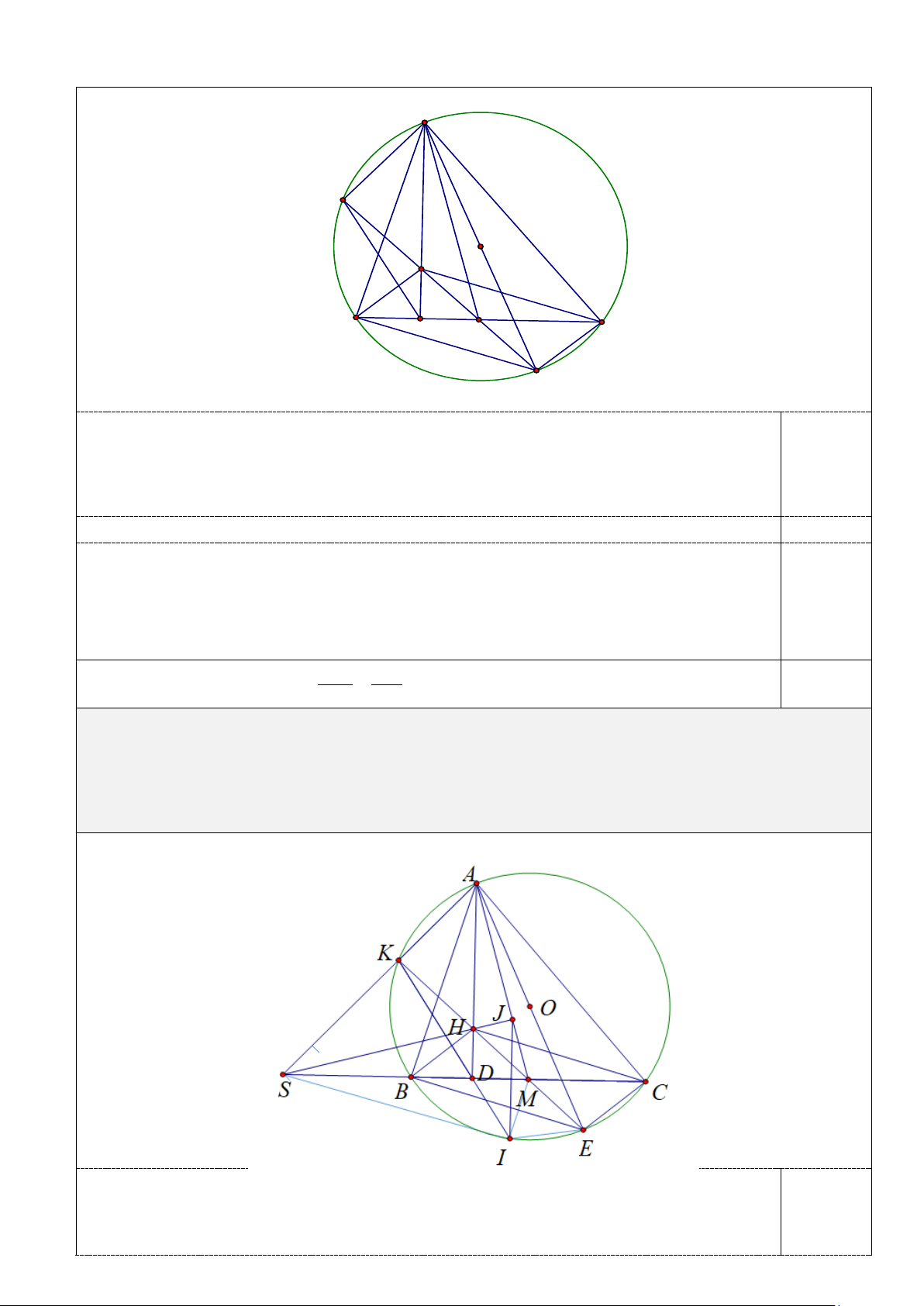
4.(1,0 điểm) Một đường tròn thay đổi luôn tiếp xúc với AK tại A và cắt các cạnh AB, AC lần
lượt tại P, Q phân biệt. Gọi N là trung điểm của đoạn thẳng PQ . Chứng minh rằng đường
thẳng AN luôn đi qua một điểm cố định. A K O' P N ≡ N' O Q H B D M C E
Gọi N ' là giao điểm của PQ và AE. Xét A ∆ QN ' và B ∆ EM có:  = 
QAN ' EBM ;  =  =  AQN ' KAP BEM ⇒ ∆ ∽ ∆ ( ) AN ' ' . BM AQN BEM g g ⇒ = (5) QN ' EM 0,25 Do  = 
QAN ' EBM ;  =  = 
AQN ' KAP BEM nên theo tính chất góc ngoài của A ∆ QN ' và 0,25 B
∆ EM ta có  =  EMC PN ' A . 6 Mà  = 
PAN ' ECM nên E ∆ CM CM AN ' ∽ P
∆ AN ' (g.g) ⇒ = . (6) EM PN ' 0,25
Từ (5) và (6) và kết hợp BM = CM AN ' AN ' ⇒ =
⇒ QN ' = PN ' ⇒ N ≡ N '. QN ' PN '
Vậy AN luôn đi qua một điểm cố định O . 0,25
Câu V. (1,0 điểm)Cho a,b,c là ba số thực dương thỏa mãn điều kiện 1 1 1 + + = 1. 2 2 2 a b c
Tìm giá trị lớn nhất của biểu thức: 1 1 1 P = + + . 2 2 2 2 2 2
5a + 2ab + 2b
5b + 2bc + 2c
5c + 2ca + 2a
Với a,b,c > 0, chứng minh được: (a b c) 1 1 1  1 1  1 1 1  9  + + + + ≥ ⇒ ≤ + +  a b c
a b c 9  a b c  + +  (x y z)2 2 2 2 1 1 1  1 1 1 3(x y z ) 3  + + ≤ + + ⇒ + + ≤ + +  2 2 2 a b c a b c    0,25
Với a,b > 0 , ta có : 2 2 2 2 2 2
5a + 2ab + 2b = (4a + 4ab + b ) + (a − 2ab + b ) 2 2 2
= (2a + b) + (a − b) ≥ (2a + b) 2 2 2
⇒ 5a + 2ab + 2b ≥ (2a + b) = 2a + b 0,25 1 1 1  1 1 1  1  2 1  ⇒ ≤ ≤ + + = +     2 2
5a + 2ab + 2b
2a + b 9  a a b  9  a b Tương tự: 1 1  2 1  1 1  2 1 ;  ≤ + ≤ +     2 2 2 2
5b + 2bc + 2c 9  b c
5c + 2ca + 2a 9  c a 0,25
1  2 1 2 1 2 1  1  1 1 1  1  1 1 1  1 3 P ≤ + + + + + = + + ⇒ P ≤ ⋅ 3 + + = ⋅  3 =      2 2 2
9  a b b c c a  3 a b c  3  a b c  3 3
a = b = c Dấu “=” xảy ra  ⇔  1 1 1
⇔ a = b = c = 3 + + =  1 2 2 2 a b c Vậy 3 max P =
khi a = b = c = 3 . 3 0,25 --HẾT--
Document Outline

  • Đề toán 10 chuyên năm 2023-2024
  • Đáp án đề toán 10 chuyên năm 2023-2024