Đề tuyển sinh lớp 10 chuyên môn Toán (chuyên Tin) 2022 – 2023 sở GD&ĐT Quảng Nam

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 VÀO TRƯỜNG TỈNH QUẢNG NAM
THPT CHUYÊN NĂM HỌC 2022-2023
Môn thi: TOÁN (Toán chuyên Tin) ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề thi gồm có 01 trang) Khóa thi ngày: 14-16/6/2022 Câu 1. (1,5 điểm)  a  a   a  a  Cho biểu thức A  1 1  với a  0, a  1.  a 1    a 1   
Rút gọn A và tìm a sao cho 2 A  A  0 . Câu 2. (1,0 điểm)
Tìm tất cả các số nguyên dương n để 4 2
n  3n 1 là số nguyên tố. Câu 3. (1,0 điểm) Cho parabol 2
(P) : y  x và đường thẳng d : y  2x  m ( m là tham số). Tìm tất
cả các giá trị của m để d cắt (P) tại hai điểm phân biệt sao cho một trong hai giao điểm
đó có hoành độ bằng 1. Câu 4. (2,0 điểm) a) Cho phương trình 2
x  6x  m  0 . Tìm tất cả các giá trị nguyên của tham số m để
phương trình đã cho có hai nghiệm phân biệt x ; x thoả mãn 2 2 2x  x x  2x  38 . 1 2 1 1 2 2  1  2x  4y  5 x  2y
b) Giải hệ phương trình  . x  2y   3  x  2y Câu 5. (3,5 điểm)
Cho đường tròn (O) và điểm I nằm ngoài đường tròn đó. Từ điểm I kẻ hai tiếp tuyến I ,
A IB với đường tròn (O) ( , A B là các tiếp điểm).
a) Chứng minh tứ giác OAIB nội tiếp đường tròn.
b) Qua A kẻ đường thẳng song song với IB cắt đường tròn (O) tại điểm thứ hai là C (C
khác A). Đường thẳng IC cắt đường tròn (O) tại điểm thứ hai là E (E khác C). Đường
thẳng AE cắt IB tại K. Chứng minh 2 KB  AK.KE . IE DE
c) Đường thẳng IC cắt AB tại D. Chứng minh  . IC DC Câu 6. (1,0 điểm) 2 2 x y  x y Chứng minh rằng   4  3 
với mọi số thực x; y khác 0. 2 2 y x  y x  
--------------- HẾT ---------------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh: .................................................................. Số báo danh: ...........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 VÀO TRƯỜNG TỈNH QUẢNG NAM
THPT CHUYÊN NĂM HỌC 2022-2023 HDC CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN TOÁN CHUYÊN TIN
(Bản hướng dẫn này gồm 04 trang) * Lưu ý:
Nếu thí sinh làm bài không theo cách nêu trong hướng dẫn chấm nhưng đúng thì vẫn cho đủ
số điểm từng phần như hướng dẫn quy định. Câu Nội Dung Điểm  a  a   a  a  Cho biểu thức A  1 1 
với a  0, a  1 . Rút gọn A và  a 1    a 1    1,5 tìm a sao cho 2 A  A  0 .  a( a 1)  a( a 1) A  1 1     0,25 Câu 1  a 1   a 1   1 a1 a  0,25
Kết quả: A  1 a với a  0; a  1 0,25  A  0 1   a  0 a  1 0,25 + 2 A  A  0     0,25  A 1 1   a 1       a  2
Đối chiếu điều kiện, chọn a  2 0,25
Tìm tất cả các số nguyên dương n để 4 2
n  3n 1 là số nguyên tố. 1,0
B  n  n   n  2 4 2 2 2  n   2 n  n   2 3 1 1 1 n  n   1 . 0,25 Câu 2 Với n  1, ta có B  1
 không phải là số nguyên tố. 0,25
Với n  2 , ta có B  5là số nguyên tố. 0,25
Với n  2 , mỗi thừa số của B đều lớn hơn 1 nên B là hợp số. 0,25 Vậy n  2 thoả đề. Cho parabol 2
(P) : y  x và đường thẳng d : y  2x  m ( m là tham số).
Tìm tất cả các giá trị của m để d cắt (P) tại hai điểm phân biệt sao cho một 1,0
trong hai giao điểm đó có hoành độ bằng 1. Câu 3
Phương trình hoành độ giao điểm của (P) và d là 2 x  2x  m  0 0,25
(P) và d  cắt nhau tại hai điểm phân biệt '
   1 m  0  m  1 . 0,25
Gọi A là giao điểm có hoành độ bằng 1, A P nên ( A 1; 1) 0,25 A d  1
  2  m  m  3 (thoả mãn). Vậy m  3  . 0,25 Câu 4 a) Cho phương trình 2
x  6x  m  0 . Tìm tất cả các giá trị nguyên của 1,0 ( 2,0 )
tham số m để phương trình có hai nghiệm phân biệt x ; x 1 2 thoả mãn 2 2 2x  x x  2x  38 . 1 1 2 2 '   9  m , 0,25
phương trình có 2 nghiệm phân biệt x ; x  9  m  0  m  9 . 1 2 0,25
2x  x x  2x  38  2x  x 2 34 2 2 2
 5x x  38  2.6  5m  38  m  1 1 2 2 1 2 1 2 . 0,25 5 34 Vậy  m  9  m 7;  8 do m là số nguyên. 0,25 5  1  2x  4y  5 x  2y
b) Giải hệ phương trình  x  2y . 1,0   3  x  2y 1 u  2v  5
Điều kiện x  2 y . Đặt u  ; v  x  2 .
y Ta có hệ phương trình  x  2y uv  3 0,25  3
Giải tìm được u  3; v   1 hoặc u  2; v    .  0,25 2  2  1 x  x  2y   0,25 - Với u  3; v   1 , ta có 3  3   1 x  2y 1  y   6  1 x  2y  x  1  3   - Với 2 u  2; v    , ta có   .   1 2 3 y  x 2y     4  2  2 0,25 x   x  1  
Đối chiếu điều kiện, hệ phương trình đã cho có 2 nghiệm 3  ;  1 1  y  y     4 6
 Nếu thiếu điều kiện x  2y thì trừ 0,25 đ Cho đường tròn ( )
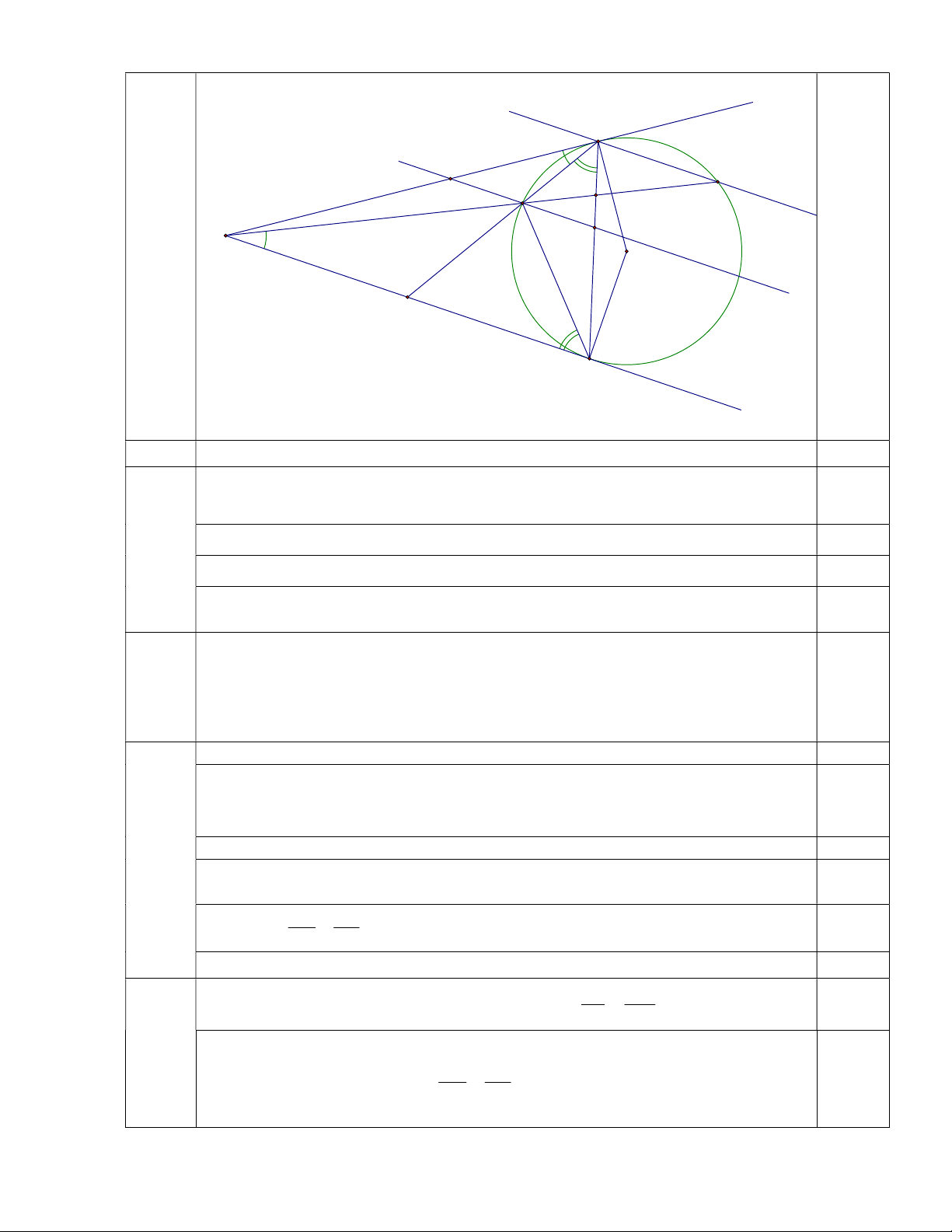
O và điểm I nằm ngoài đường tròn đó. Từ điểm I kẻ hai tiếp tuyến I , A IB với đường tròn ( ) O ( , A B là các tiếp điểm).
a) Chứng minh tứ giác OAIB nội tiếp đường tròn.
b) Qua A kẻ đường thẳng song song với IB cắt đường tròn (O) tại Câu 5
điểm thứ hai là C (C khác A). Đường thẳng IC cắt đường tròn ( ) O 3.5
tại điểm thứ hai là E (E khác C). Đường thẳng AE cắt IB tại K. Chứng minh 2 KB  AK.KE . IE DE
c) Đường thẳng IC cắt AB tại D. Chứng minh  . IC DC A J C D E I H O K B 5a
a) Chứng minh tứ giác OAIB nội tiếp đường tròn 1,0
Hình vẽ phục vụ câu a) 0,25  0
IAO  90 (tính chất tiếp tuyến) 0,25  0
IBO  90 (tính chất tiếp tuyến) 0,25 Suy ra  IAO   0
IBO  180 nên tứ giác OAIB nội tiếp đường tròn. 0,25
b) Qua A kẻ đường thẳng song song với IB cắt đường tròn (O) tại
điểm thứ hai là C (C khác A). Đường thẳng IC cắt đường tròn ( ) O 5b 1,5
tại điểm thứ hai là E (E khác C). Đường thẳng AE cắt IB tại K. Chứng minh 2 KB  AK.KE .
Hình vẽ phục vụ câu b) 0,25
Xét hai tam giác AKB và BKE, có  KAB  
KBE (cùng bằng nửa số đo của cung EB), 0,25 góc K chung 0,25 nên chúng đồng dạng 0,25 AK KB suy ra  . 0,25 BK KE 2  KB  AK.KE 0,25 IE DE
c) Đường thẳng IC cắt AB tại D. Chứng minh  . 1,0 IC DC 5c
Xét hai tam giác AKI và IKE, có  KAI  
KIE (cùng bằng góc ECA), góc K chung AK IK
nên chúng đồng dạng, suy ra 2   IK  AK.KE . 0,25 IK KE
Từ đó suy ra IK  KB (1)
Qua E kẻ đường thẳng song song với IB, cắt AB tại H và cắt IA tại J, theo JE EH định lí Ta-lét ta có  (2). 0,25 IK KB JE EH
Từ (1) và (2) suy ra JE  EH   . 0,25 AC AC IE JE DE EH IE DE Theo định lí Ta-let  và  . Vậy  . 0,25 IC AC DC AC IC DC 2 2 x y  x y  Chứng minh rằng   4  3 
với mọi số thực x; y khác 0. 1,0 2 2 y x  y x   Cách 1: x y  x y x  y  4x y 3 2 2 2 2 4 4 2 2 x  y    4  3    2 2   2 2 y x  y x  x y xy 0,25 4 4 2 2
 x  y  4x y  3xy  2 2 x  y  2 2 (do x y  0)  x  y 2 2 2   2 2 x  y  2 2 xy  x y  xy  2 2 2 2 x  y   0 0,25   2 2 x  y  2 2
x  y  xy  2xy  2 2 x  y  xy  0 0,25   2 2 x  y  xy 2 2 x  y  2xy  0 2 2  y 3y    2 Câu 6   x      x  y  0 (*)  0,25 2  4  
Bất đẳng thức (*) luôn đúng với mọi số thực x; y khác 0. Vậy bất đẳng thức đã cho
luôn đúng với mọi số thực x; y khác 0. Cách 2: x y 2 2 2  x y x y Đặt t   . Ta có 2 t      2 y x   2 2  y x  y x 2 2 x y t  2 Theo Cô-si 2   2  t  4  0,25 2 2 y x  t  2
Bất đẳng thức đã cho trở thành 2
t  3t  2  0  t   1 t  2  0 (*) 0,25
Với t  2 , (*) luôn đúng nên bất đẳng thức đã cho luôn đúng 0,25 Với t  2
 , (*) luôn đúng nên bất đẳng thức đã cho luôn đúng 0,25
---------------------------------------------------------------