Đề tuyển sinh lớp 10 chuyên môn Toán (chuyên Toán) năm 2021 – 2022 sở GD&ĐT Quảng Nam

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM NĂM HỌC 2021 - 2022
Môn thi: TOÁN (Chuyên Toán) ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (Không kể thời gian phát đề)
Khóa thi ngày: 03 - 05/6/2021 Câu 1: (2,0 điểm)
8  x 1 x 2 x 1 x  3 x
a) Rút gọn biểu thức A  
(với x  1, x  4, x  9 )
x  4x 2 x  4 2x  x 6
b) Tìm tất cả bộ ba số nguyên tố ,
p q, r thỏa mãn pq  r 1 và  2 2 p  q  2 2  r 1.
Câu 2: (1,0 điểm) Cho parabol (P): 2
y  x và đường thẳng (d) y  2  2m x  m (m là tham số). Chứng  1 
minh rằng (d) luôn cắt (P) tại hai điểm A, B sao cho M ;1 
 là trung điểm của đoạn thẳng AB, hai  2 
điểm H, K lần lượt là hình chiếu vuông góc của A, B trên trục hoành. Tính độ dài đoạn thẳng KH. Câu 3: (2,0 điểm)
a) Giải phương trình  x   2 1 7  2x  x  3x  2 . x  2y  xy  2  0
b) Giải hệ phương trình  . 2 2 2 2
x  y  2x y  2xy 1  0 Câu 4: (2,0 điểm).
Cho hình vuông ABCD tâm O, điểm E nằm trên đoạn thẳng OB (E khác O, B), H là hình chiếu
vuông góc của C trên đường thẳng AE. Gọi F là giao điểm của AC và DH.
a) Chứng minh HD là tia phân giác của góc AHC.
b) Chứng minh diện tích hình vuông ABCD bằng hai lần diện tích tứ giác AEFD. Câu 5: (2,0 điểm).
Cho tam giác nhọn ABC (AB < AC). Đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F, E.
Gọi H là giao điểm của BE và CF, đường thẳng AH cắt BC tại D.
a) Chứng minh tứ giác ODFE nội tiếp đường tròn.
b) Gọi K là giao điểm của AH và EF, I là trung điểm của AH. Đường thẳng CI cắt đường tròn (O) tại
M (M khác C). Chứng minh CI vuông góc với KM.
Câu 6: (1,0 điểm). Cho ba số thực dương x, ,
y z thỏa mãn xy  yz  zx  xyz . Tìm giá trị nhỏ nhất của biểu 2 2 2 x y z thức H    . 2 2 2 9z  zx 9x  xy 9y  yz
--------------------------------------------
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: (2,0 điểm)
8  x 1 x 2 x 1 x  3 x
a) Rút gọn biểu thức A  
(với x  1, x  4, x  9 )
x  4x 2 x 4 2x  x 6
b) Tìm tất cả bộ ba số nguyên tố ,
p q, r thỏa mãn pq  r 1 và  2 2 p  q  2 2  r 1. Lời giải
8  x 1 x 2 x 1 x  3 x
a) Rút gọn biểu thức A  
(với x  1, x  4, x  9 )
x  4x 2 x 4 2x  x 6
Với x  1, x  4, x  9 ta có:
8  x 1 x 2 x 1 x  3 x A  
x  4x 2 x  4 2x  x 6   8  x 1  x   21  x    x 3   
x  2 x  2x  2 x  4 2 x 3 x  2 8  x 1 x 1 x  x 3   
x  2x x 8 2 x 3 x  2 8  x x x   
x  2x x 8 2 x  2 1 x    x  2 2 x  2
2 x  2  x  x  2  2 x  2 x  2 x  4  2 x  4
b) Tìm tất cả bộ ba số nguyên tố , p ,
q r thỏa mãn pq  r 1 và  2 2 p  q  2 2  r 1. S  p  q Đặt  ta có hệ: P  . p q P  r 1 P  r 1 P  r 1 P  r 1                S  P  r   S  P 2 2 2 2 2 2 r 4r 5 2 r  4r  5 2 2 1 2 2  r 1 S  S   2  2 r  5 r  5 r  5 r  5     Vì , p ,
q r là ba số nguyên tố nên ta có: S  5  p  q  5  q  5  p  q  5 p P  6  .pq  6    . p  5  p  2  6  p  5p  6  0 r  5 r  5   
 p  2 hoặc  p  3 q  3   q  2 
Câu 2: (1,0 điểm) Cho parabol (P): 2
y  x và đường thẳng (d) y  2  2m x  m (m là tham số). Chứng  1 
minh rằng (d) luôn cắt (P) tại hai điểm A, B sao cho M ;1 
 là trung điểm của đoạn thẳng AB, hai  2 
điểm H, K lần lượt là hình chiếu vuông góc của A, B trên trục hoành. Tính độ dài đoạn thẳng KH. Lời giải
Phương trình hoành độ giao điểm của (P) và (d): 2 x  2  2m x  m 2
 x  2  2m x  m  0   1
  2  2m2  4.1.m  4m  4m  4  2m  2 2 1  3  0 m 
Do đó phương trình (1) luôn có hai nghiệm phân biệt với mọi m nên (d) luôn cắt (P) tại hai điểm
phân biệt A, B với mọi giá trị của m.
Với mọi m, theo định lý Vi-et ta có:  b x  x   2  2m  1 2  a  c x .x   m 1 2  a  1  x  x 2  2m 1 1 Vì M ;1 
 là trung điểm của đoạn thẳng AB nên 1 2    m   2  2 2 2 2  1 3 2  3 x   y  1 1
Thay m  vào (1) ta có phương trình: 2 2 2 x  x   0   2 2  1 3 2  3 x   y   2 2
1 3 2  3  1 3 2  3   A ; , B  ;   2 2   2 2       1 3  1 3 
Vì H, K là hình chiếu của A, B lên trục hoành nên  H  ;0, K  ;0  2   2      1 3 1 3  HK    3 2 2 Câu 3: (2,0 điểm)
a) Giải phương trình  x   2 1 7  2x  x  3x  2 . x  2y  xy  2  0
b) Giải hệ phương trình  . 2 2 2 2
x  y  2x y  2xy 1  0 Lời giải 7
a) Giải phương trình  x   2
1 7  2x  x  3x  2 . Điều kiện: x  2  x   1 7  2x   x   1  x  2  x   1 7  2x  x   1  x  2  0  x  
1  7  2x  x  2  0 x  1 x  1 x 1  0      x  2   x  2   7  2x  x  2    7  2x   x 22 2
x  2x 3  0 x  1 x  2 x  1     x 3    x  3  x  1 
Vậy tập nghiệm của phương trình: S  1;  3 x  2y  xy  2  0   1
b) Giải hệ phương trình  2 2 2 2
x  y  2x y  2xy 1  0  2
Giải (1) ta có: x  2y  xy  2  0
 x 1 y  21 y  0
 x 1 y  21 y  0
 1 yx  2  0 x  2   y  1
Với x = 2 thay vào phương trình (2) ta có: 2 2
4  y  8y  4y 1  0 2  3y  8y  5  0 y  1    5 y   3
Với y = 1 thay vào phương trình (2) ta có: x  0 2 2 2 x 1 2x 2x 1 0 3x 2x 0           2 x   3   5    2  
Vậy nghiệm của hệ phương trình là:  x; y   2;  1 ; 2; ;   0;  1 ; ;1     3   3  Câu 4: (2,0 điểm).
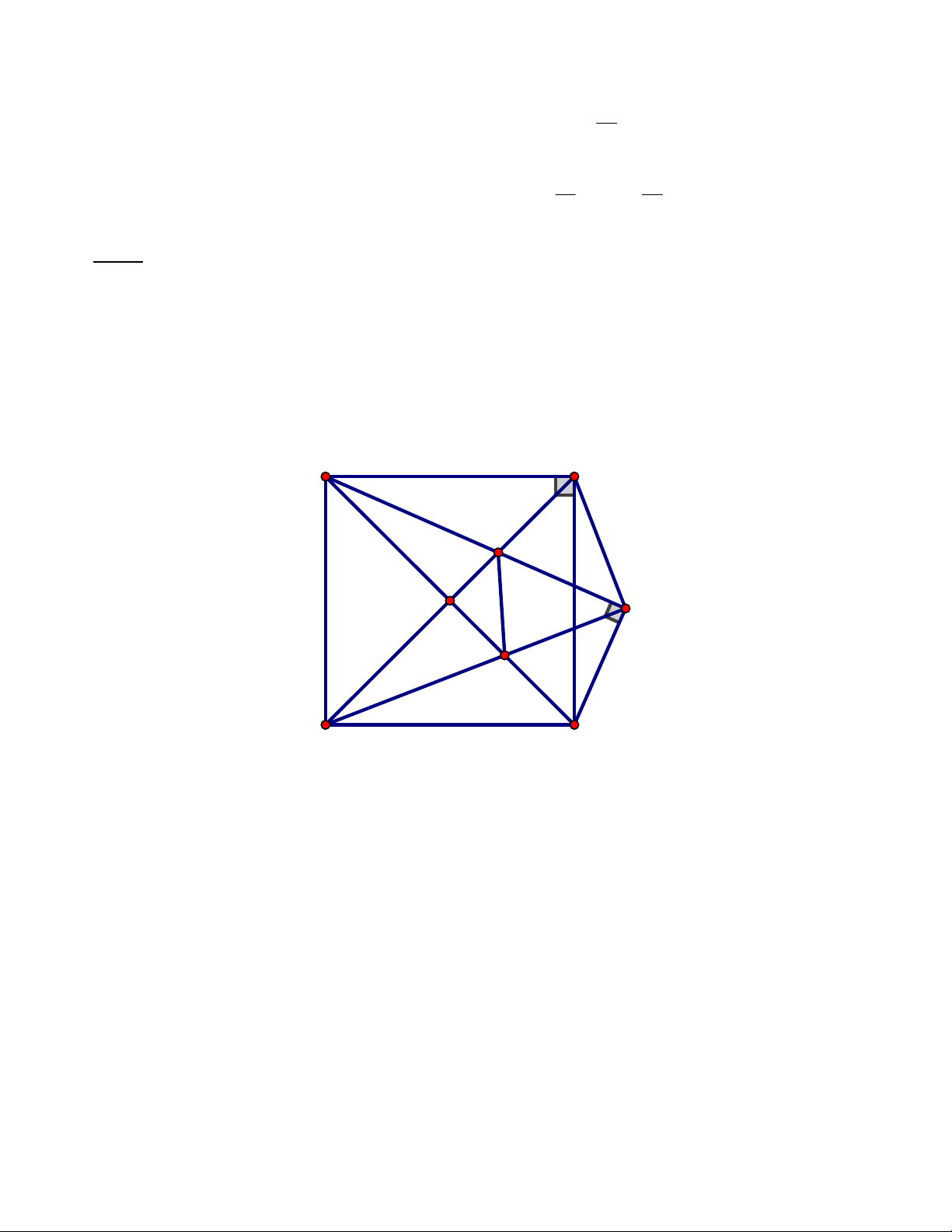
Cho hình vuông ABCD tâm O, điểm E nằm trên đoạn thẳng OB (E khác O, B), H là hình chiếu
vuông góc của C trên đường thẳng AE. Gọi F là giao điểm của AC và DH.
a) Chứng minh HD là tia phân giác của góc AHC.
b) Chứng minh diện tích hình vuông ABCD bằng hai lần diện tích tứ giác AEFD. Lời giải A B E H O F D C a) Ta có  0
ADC  90 (ABCD là hình vuông)  0
AHC  90 (H là hình chiếu của C trên AE) Xét tứ giác ADCH có:  ADC   0 AHC  180
Mà hai góc này ở vị trí đối nhau
 Tứ giác ADCH nội tiếp.   DAC   0
DHC  45 (cùng chắn cung CD) mà  AHD   0 DHC  90   0 AHD  45
 HD là tia phân giác của góc AHC. b) Xét tứ giác OEHC có:  EOC   0 EHC  180
Mà hai góc này ở vị trí đối nhau
 Tứ giác OEHC nội tiếp.   AEO  
ACH (góc ngoài bằng góc đối trong) (1)
Tứ giác ADCH nội tiếp (cmt)   ADF  
ACH (cùng chắn cung AH) (2)
Từ (1) và (2) suy ra   AED   ADF Xét ADE và FAD có:  ADE  FAD 0 =  45    ADE ∽ F  ADg.g  AED   ADF cmt  AF AD 2    A . F DE  AD AD DE 1 1 1 Ta có: 2 S  AF.DE  AD  S AEFD 2 2 2 ABCD Câu 5: (2,0 điểm).
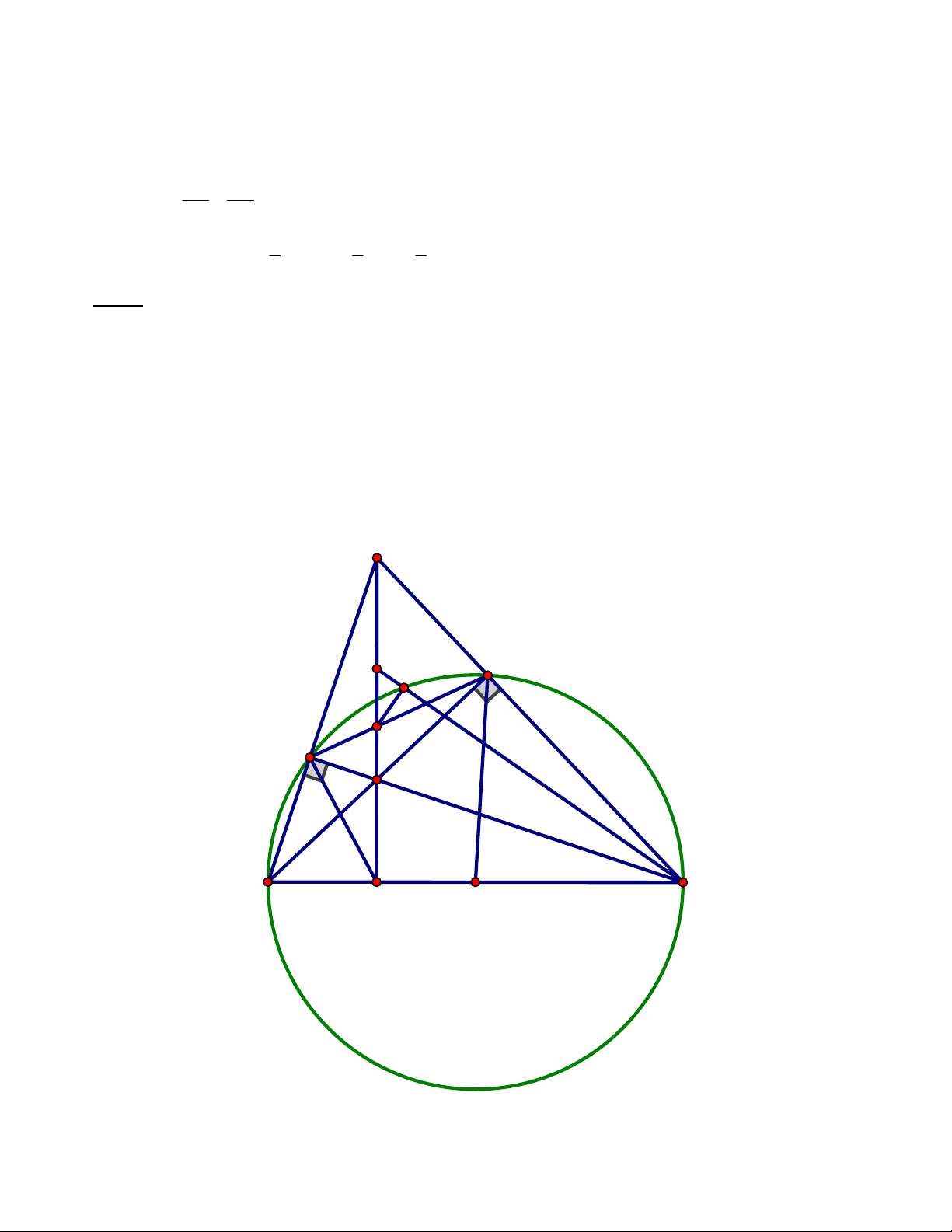
Cho tam giác nhọn ABC (AB < AC). Đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F, E.
Gọi H là giao điểm của BE và CF, đường thẳng AH cắt BC tại D.
a) Chứng minh tứ giác ODFE nội tiếp đường tròn.
b) Gọi K là giao điểm của AH và EF, I là trung điểm của AH. Đường thẳng CI cắt đường tròn (O) tại
M (M khác C). Chứng minh CI vuông góc với KM. Lời giải A I M E K F H B C D O a) Ta có  0
BFC  90 (góc nội tiếp chắn nửa đường tròn)  0
BEC  90 (góc nội tiếp chắn nửa đường tròn)
Xét tam giác ABC có: BE và CF là 2 đường cao cắt nhau tại H  H là trực tâm tam giác ABC.  AH  BC tại D.
Ta có tứ giác BCEF nội tiếp (O)   AFE  
OCE (góc ngoài bằng góc đối trong). Xét tứ giác ACDF có:  0 ADC  90 (cmt)  0 AFC  90 (cmt)
 tứ giác ACDF nội tiếp   BFD  
OCE (góc ngoài bằng góc đối trong).
Xét tam giác BEC vuông tại E có EO là trung tuyến 1
 EO  BC  CO  BO (định lý đường trung tuyến của tam giác vuông) 2   OCE   OEC   0 COE  180  2 OCE  AFE    OCE cmt Ta có    0 COE  180   AFE   BFD    EFD BFD    OCE cmt  Xét tứ giác ODFE có  COE   EFD cmt 
Mà hai góc ở vị trí góc ngoài và góc đối trong  tứ giác ODFE nội tiếp. b)
Xét tam giác AEH vuông tại E có EI là trung tuyến 1
 EI  AH  AI  HI (định lý đường trung tuyến của tam giác vuông) 2   IAE   IEA, có  OCE   OEC cmt và  IAE phụ  OCE   IEA phụ  OEC   0 OEI  90
Chứng minh tương tự ta có  0 OFI  90 Xét tứ giác OEIF có  OEI   0 OFI  180
Mà hai góc ở vị trí đối nhau  tứ giác OEIF nội tiếp.
Ta có tứ giác ODFE nội tiếp (cmt), tứ giác OEIF nội tiếp (cmt)  5 điểm O, D, F, I, E cùng thuộc
đường tròn đường kính ID. Xét I  EK và IDE có:  DIE chung      ∽  IDK   IDE    ECF IEK IDE g.g  IE IK 2    IE  I . D IK   1 ID IE Xét IEM và ICE có:  ICE chung        ∽  IEM   IEM ICE g. 1 g ICE  sd cung EM    2  IE IM 2    IE  I . C IM 2 IC IE IK IC
Từ (1) và (2)  IK.ID  I . C IM   IM ID Xét IMK và IDC có:  DIC chung   I  MK ∽ I  DC  .cg.c   IMK   IDC 0 0 IK IC mà  IDC  90   IMK  90  CI  KM   IM ID 
Câu 6: (1,0 điểm). Cho ba số thực dương x, ,
y z thỏa mãn xy  yz  zx  xyz . Tìm giá trị nhỏ nhất của biểu 2 2 2 x y z thức H    . 2 2 2 9z  zx 9x  xy 9y  yz Lời giải 1 1 1
Theo đề ta có:    1 x y z 1 1 1
Đặt  a ,  b ,  c  , a ,
b c  0  a  b  c  1 x y z c a b Khi đó H    2 2 2 9a 1 9b 1 9c 1 c  2 9a   2 2 1  9a c c 9a c Ta có:   c  2 2 2 9a 1 9a 1 9a 1 2 2 9a c 9a c 3 Vì 2 9a 1  6a  c   c   c  ac 2 9a 1 6a 2 a 3 b 3
Chứng minh tương tự ta có:  a  ba ;  b  cb 2 9b 1 2 2 9c 1 2 3
 H  a  b  c  ab  bc  ca 2 a  b c2 Mà ab  bc  ca  3 3 1 1  H  1 .  2 3 2 1 Vậy H
 . Dấu bằng xảy ra khi và chỉ khi x  y  z  3 min 2
--------------------------------------------