Đề tuyển sinh lớp 10 chuyên môn Toán năm 2025 – 2026 sở GD&ĐT Quảng Trị

CLB Toán Cơ Sở Phòng Nội Dung
HƯỚNG DẪN GIẢI ĐỀ THI CHUYÊN TOÁN QUẢNG TRỊ Năm học 2025 - 2026 Câu 1: a. ĐKXĐ: a  , 0 a  . 1 Ta có:  1 3 a  5   a 1 1   1 3 a  5   a 1 2 a  P   .     .
 a 1 a a  a  a 1    4 a 2   a 1 ( a  )( 1 a  ) 1   4 a     
 a 1 3 a  5  ( a  ) 1 2 4( a  )( 1 a  ) 1 2 1  .   .  ( a  )( 1 a  ) 1  4 a ( a  ) 1 2 ( a  4 ). 1 a a   b. Thật vậy, ta có 3 1 
 3 a  a  a 1  0  ( a  ) 1 2,a  , 0 a  . 1 a  a 1 a Câu 2:
1. Gọi số giáo viên nam trong trường là x, thì số giáo viên nữ là 80 - x (người).
Tổng số tuổi của tất cả 80 giáo viên là 80.45 = 3600.
Tổng số tuổi của tất cả giáo viên nam và nữ lần lượt là: 50x và (80 - x).42. Khi đó: 50x  80 (  x) 42 .  3600  x  30.
Như vậy số giáo viên nam là 30, thì số giáo viên nữ là 50 (người). 1
2. ĐKXĐ: 1  x   . Ta đặt 4x 1  a, 1 x  , b (a,b  ). 0 4
Khi đó phương trình ban đầu trở thành: a  2
a  2b  2  ab  (a  2)(b  ) 1  0  .  b  1 3
Trường hợp 1: a = 2. Ta có: 4x 1  2  x  , (thoả mãn). 4
Trường hợp 2: a = 1. Ta có: 1 x 1  x  , 0 (thoả mãn). Câu 3: 150
1. Giả sử độ dài cung tròn AB trên hình vẽ là a, thì a  .24  20 (cm). 180
Ở hình vẽ 2, ta có chu vi đáy của hình nón là a.
Khi đó, gọi bán kính đáy là r, thì ta có: a  2r  r  ( 10 c ). m
Và độ dài đường sinh của hình nón là OA = 24 cm. CLB Toán Cơ Sở Phòng Nội Dung
Theo định lý Pitago, ta có chiều cao h hình nón là: 2 2 2
h  r  OA  h  242 102  2 119(cm).
Vậy chiều cao hình nón: 2 119(cm). 2.
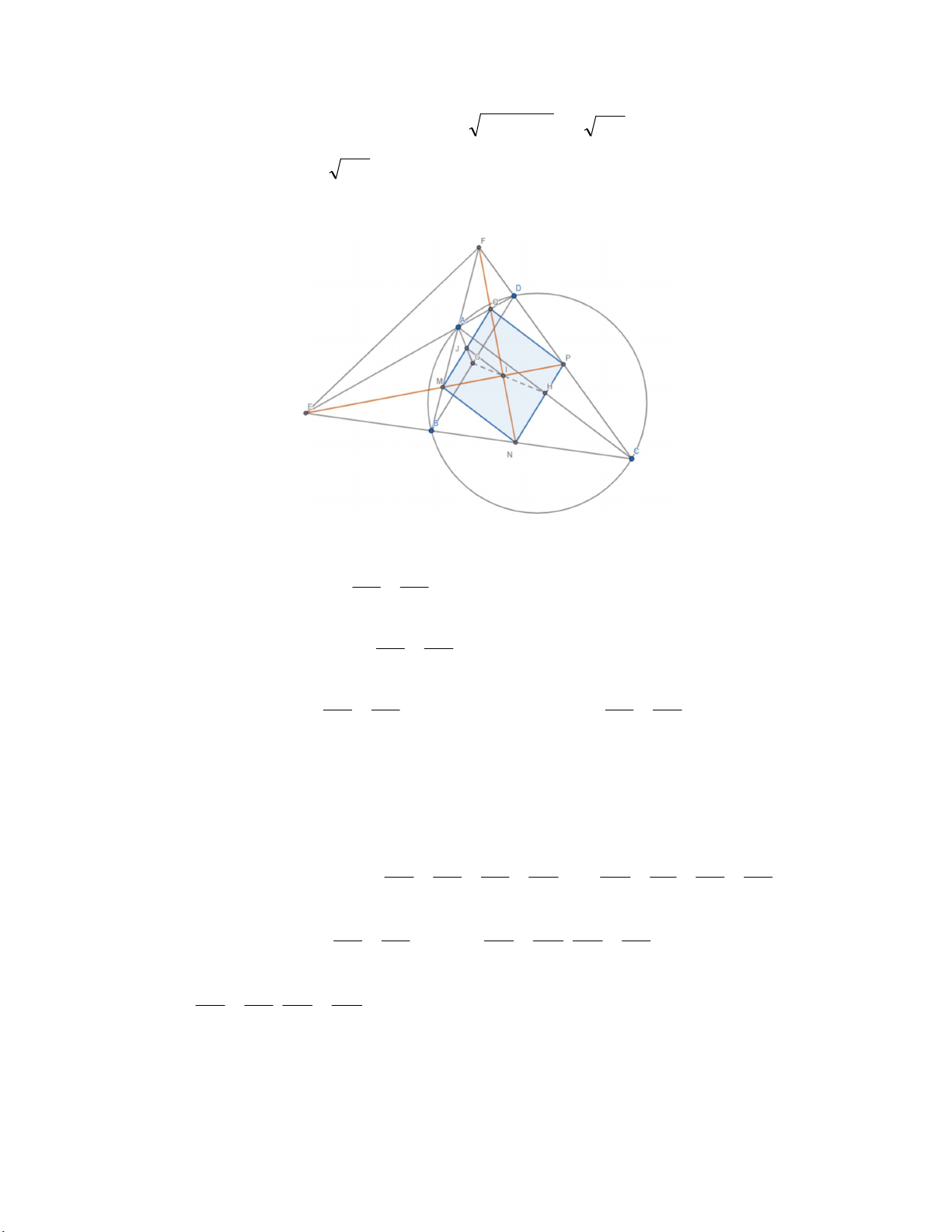
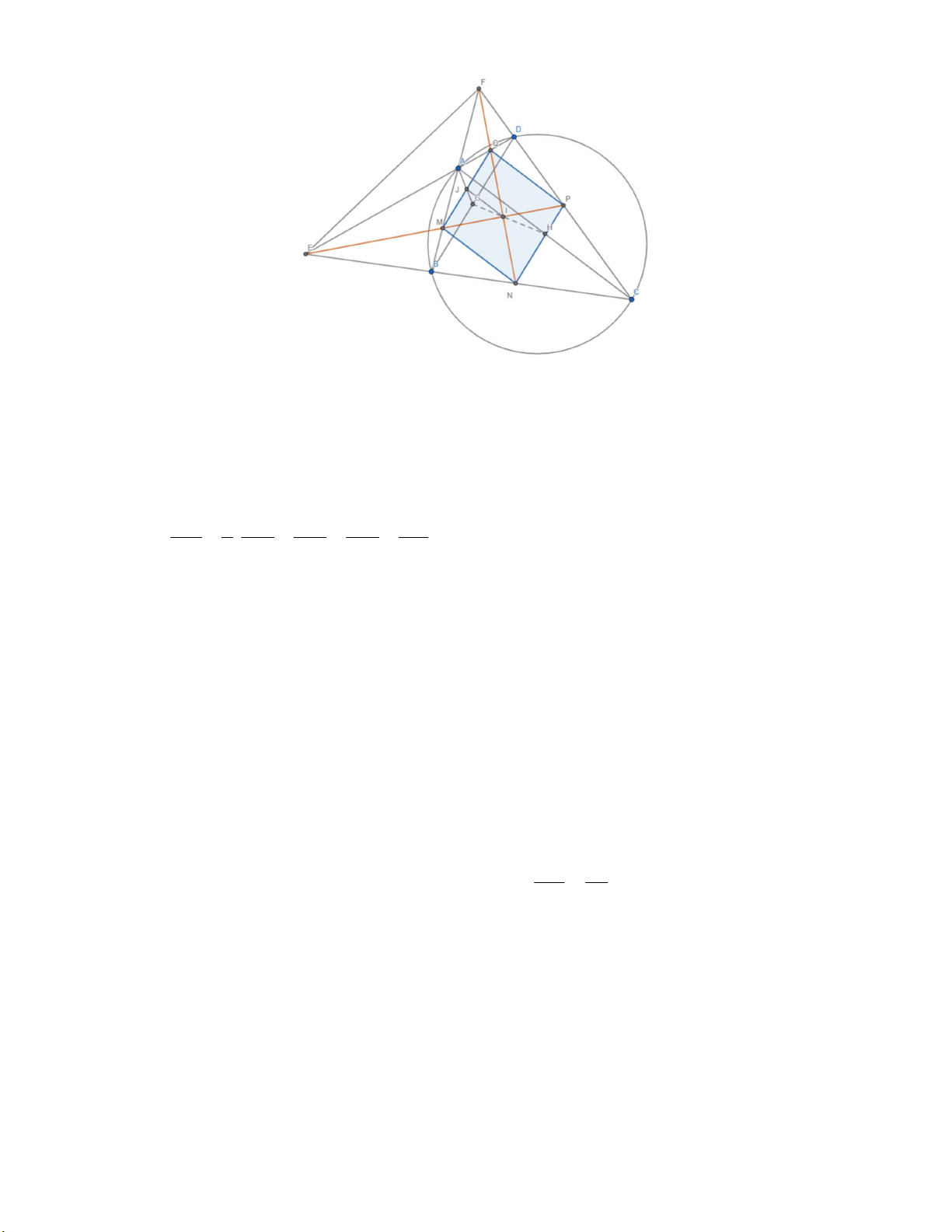
a. Do tứ giác ABCD nội tiếp nên EA  B 180  BA  D  D  CB , kết hợp với D  EC chung. EA EB Suy ra E  AB ~ E  CD(g.g)   , D  EC chung. EC ED ED BD Khi đó: E  BD ~ E  AC( . c g.c)   . (1) EC AC FD FB FB BD
Chứng minh tương tự thì  , F  BD ~ F  C ( A . c g.c)   . (2) FA FC FC AC
Từ (1) và (2) suy ra điều phải chứng minh. b.
i. Ta thấy MNPQ là hình thoi. Thật vậy QD FD FB NB MB EB ED PD
Theo tính chất đường phân giác:    , và    . QA FA FC NC MA EA EC PC ED FB QD MB NB PD
Mặt khác theo câu a ta có:  . Suy ra  ,   MQ | BD | N . P EC FC QA MA NC PC QD PD NB MB Tương tự  ,   PQ || AC | MN. QA PC NC MA
Như vậy MNPQ là hình bình hành. Đồng thời, do tam giác QEN có EM vừa là phân giác
vừa là trung tuyến nên EM là đường cao hay MP vuông QN. Vậy MNPQ là hình thoi. CLB Toán Cơ Sở Phòng Nội Dung
ii. Gọi I là giao của MP, NQ. Khi đó I là trung điểm của NQ, MP. Gọi G, H là trung điểm
của BD, AC. Gọi J là trung điểm MQ.
Khi đó do MQ || BD, ta dễ dàng chứng minh: A, J, G thẳng hàng. (Thales đảo)
Ta thấy IJ là đường trung bình của tam giác QMN. IJ 1 MN MN BM JG Ta có:  .     G, I, H thẳng hàng. AH 2 AH AC BA AG
Như vậy ta có giao điểm I của NQ, MP nằm trên GH.
Nhận xét: Bổ đề hình thang. Bài 4:
Xét phép thử: “An và Bình, mỗi bạn biết ngẫu nhiên một số nguyên dương không lớn hơn
10 lên bảng”. Không gian mẫu của phép thử đó là: 10.10 = 100.
a. Xét biến cố A: “Số của An viết ra bé hơn số của Bình”
Nếu Bình viết số a > 1 thì An có a - 1 khả năng để viết ra số bé hơn Bình.
Như vậy số kết quả thuận lợi là: 1 2  3  4  ...  9  45. 45 9
Như vậy xác suất để An viết số bé hơn của Bình là  . 100 20
b. Xét biến cố B: “Số của An và Bình viết ra là a và b, thoả mãn 3 3 a  b  6ab  8 là số nguyên tố.” Giả sử 3 3
p  a  b  6ab  8 là số nguyên tố. Khi đó: 3 3
p  a  b  6ab  8  (a  b  ) 2 ( 2 2
a  b  4  2a  2b  ) ab
Do a  b  2 1 a  b  2  , 2 2
p a  b  4  2a  2b  ab  . 1 Mà 2  ( 2 2 2
a  b  4  2a  2b  a ) b  (a  ) 2 2  (b  ) 2 2  (a  b)2. CLB Toán Cơ Sở Phòng Nội Dung
Suy ra hai trong ba 3 số a  , 2 b  ,
2 a  b là 1 và số còn lại là 0.
Nếu a  2  b  2 1 a  b  ,
3 a  b  0  p  3 3 2  , 8 (loại).
Nếu a  2  a  b  , 1 b  2  0  a  ,
3 b  2  p  3  2  2  . 7 ™
Tương tự a = 2, b = 3 ™.
Như vậy có hai kết quả thuận lợi cho biến cố B.
Vậy xác suất để Số của An và Bình viết ra là a và b, thoả mãn 3 3
a  b  6ab  8 là số 2 1 nguyên tố là  . 100 50 Câu 5: 2 p  p  p 1. Ta thấy
là nghiệm của phương trình 2 x  ax  b  0 nên  . a  b  . 0 q    q  q Suy ra 2 2 p  apq  bq  ,
0 nên p2 q mà (p, q) = 1 dẫn đến q = 1.
Như vậy p chia hết cho q.
2. Giả sử tồn tại x, y thoả mãn điều kiện bài toán. a c
Đặt x  , y  , với ( , a ) b  , 1 (c, d)  ,
1 a, b, c, d là các số nguyên dương. b d 1 b d bc  ad Khi đó:  1   
nguyên dương nên ac | bc  ad. x y a c ac a  | bc  ad a  | bc a  | c Do đó:       a  . c c  | bc  ad c  | ad c  | a ac Mà xy  nên bd | ac hay b | 2 a  b  , 1 do ( , a b)  . 1 bd 1 1 1 1 Tương tự d  .
1 Như vậy x, y nguyên dương. Ta có: 1     . 2 x y 1 1 1 1
Trường hợp 1:   2  x  y  . 1 (thoả mãn). x y 1 1
Trường hợp 2:  1  x  y  xy 1  (x  ) 1 (y  ) 1  x  y  . 2 (thoả mãn). x y
Như vậy các bộ (x, y) thoả mãn bài toán là: (1,1) và (2,2).
Document Outline

• Doc1
• 30. Quang Tri. De thi Chuyen Toan 2025