Đề tuyển sinh lớp 10 chuyên năm 2018 – 2019 môn Toán sở GD và ĐT Thái Bình (đề chung)

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI TUYỂN SINH LỚP 10 THPT CHUYÊN THÁI BÌNH THÁI BÌNH
NĂM HỌC 2018 – 2019 ĐỀ C HÍNH THỨC MÔN THI: TOÁN
(Dành cho tất cả các thí sinh)
Đề thi gồm 01 trang
Thời gian làm bài: 120 phút (Không kể thời gian giao đề)
Câu 1: (2,5 điểm) Cho biểu thức:  x  4  1 1 P  1 :  
với x  0; x  ; x  1; x  4 .
 x  3 x  2
 2x  3 x 1 4
a) Rút gọn biểu thức P.
b) Tìm x sao cho P  2019 . 10
c) Với x  5, tìm giá trị nhỏ nhất của T  P  . x
Câu 2: (0,75 điểm) 1 1
Cho hai đường thẳng (d1): y  mx  m và (d2): y   x 
(với m là tham số, m  0 ). Gọi m m
I( x ; y ) là tọa độ giao điểm của hai đường thẳng (d
T  x  y . 0 0
1) với (d2). Tính 2 2 0 0
Câu 3: (1,25 điểm)
Gọi x ; x là hai nghiệm của phương trình: 2
x  (2  m)x 1 m  0 (m là tham số). 1 2
a) Tìm m để x  x  2 2 . 1 2 1 1
b) Tìm m sao cho T  
đạt giá trị nhỏ nhất. 2 2 (x 1) (x 1) 1 2
Câu 4: (1,5 điểm)
a) Giải phương trình: 4x  8072  9x 18162  5 . 3 3 2
x  y  3x  6x  3y  4  0
b) Giải hệ phương trình:  2 2
x  y  3x 1
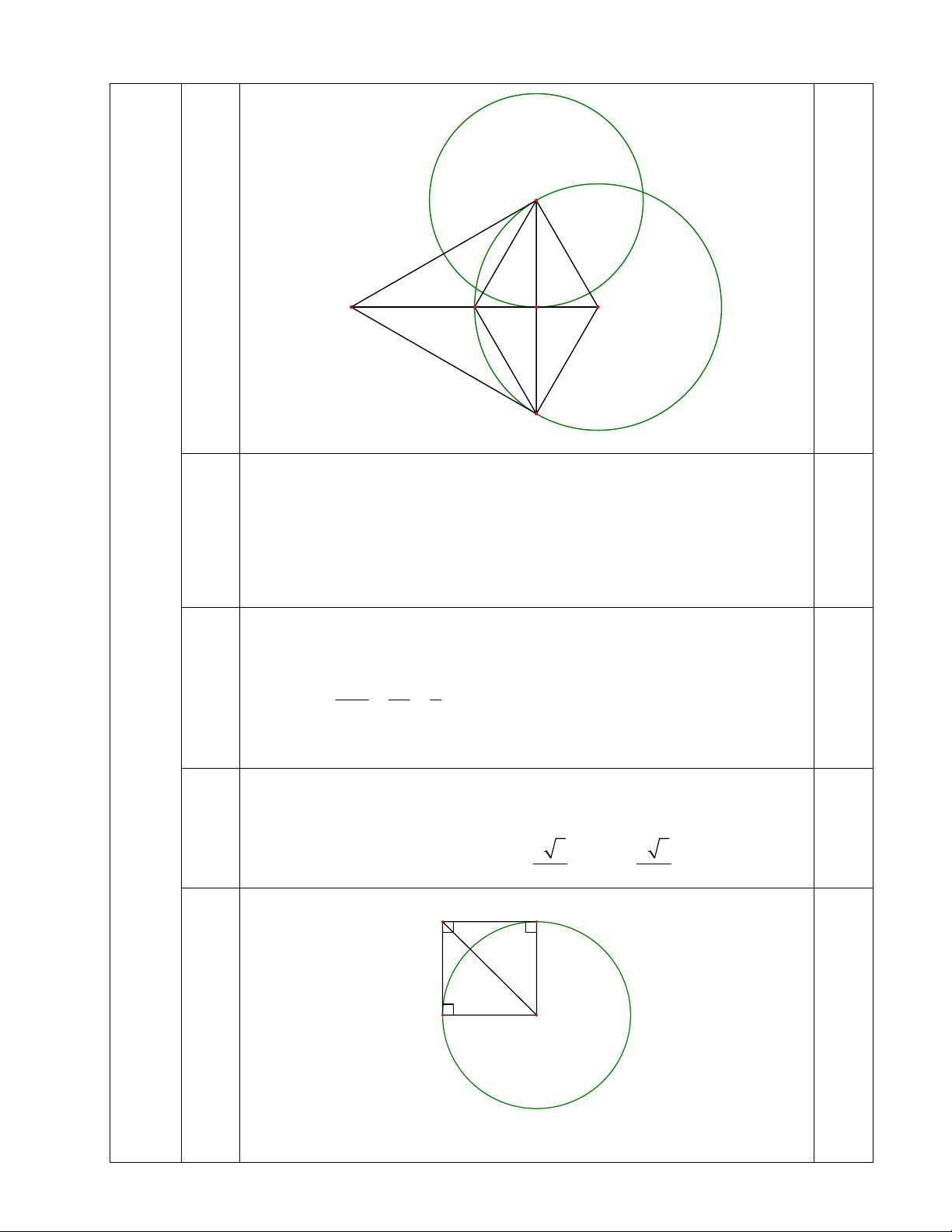
Câu 5: (3,5 điểm)
Cho đường tròn tâm O bán kính a và điểm J có JO = 2a. Các đường thẳng JM, JN theo thứ tự
là các tiếp tuyến tại M, tại N của đường tròn (O). Gọi K là trực tâm của tam giác JMN, H là
giao điểm của MN với JO.
a) Chứng minh rằng: H là trung điểm của OK.
b) Chứng minh rằng: K thuộc đường tròn tâm O bán kính a.
c) JO là tiếp tuyến của đường tròn tâm M bán kính r. Tính r.
d) Tìm tập hợp điểm I sao cho từ điểm I kẻ được hai tiếp tuyến với đường tròn (O) và hai
tiếp tuyến đó vuông góc với nhau.
Câu 6: (0,5 điểm)
Cho x, y, z là ba số thực không âm thỏa mãn: 12x 10y 15z  60 . Tìm giá trị lớn nhất của 2 2 2
T  x  y  z  4x  4y  z .
-------------------- HẾT --------------------
Họ và tên thí sinh: ....................................................
Số báo danh: .........................................
Chữ kí của giám thị 1: ..............................................
Chữ kí của giám thị 2: ..........................
HƯỚNG DẪN GIẢI VÀ BIỂU ĐIỂM DỰ KIẾN: Câu Phần Nội dung Điểm  x  4  1 P  1 :  
 x  3 x  2
 2x  3 x 1
 x  2 x  2    x x
  x   x  
 1  12  1 1 2    x  2    1 x   1 2 x   1 a) x 1   1.0
  x  2  x   1 2 x   1  2 x   1 2 x   1  4x 1 1 Câu 1
Vậy P  4x 1 với x  0; x  ; x  1; x  4 . 4 (2,5đ) 1
Với x  0; x  ; x  1; x  4 , ta có: b) 4 0.5
P  2019  4x 1  2019  x  505 (thỏa mãn ĐK)
Vậy với x  505 thì P  2019 . 10 10 2x 10 18x Xét T  P   4x 1    1 x x 5 x 5 2x 10 2x 10
Áp dụng BĐT Côsi, ta có:   2   4 5 x 5 x c) 2x 10 Dấu “=” xảy ra  
 x  5 (do x  0) 1.0 5 x 18x Lại có:  18 (vì x  5) 5
 T  4 18 1  21
Vậy minT  21 tại x  5.
Theo đề bài, ( x ; y ) là nghiệm của hệ: 0 0
y  mx  m  1 1 0 0 2 2 
mx  m   x 
m x  m  x 1 0 0 0 0  1 1   m m   y   x   
y  mx  m 0 0  0 0 y  mx    m m m 0 0 Câu 2 2  2  0.75 (0,75đ) 1 m  1  m x 2 2  0 2 x 
 m  x   m    0 2 ( 1) 1 1 m  0 1       m 2
y  m(x 1) 1 m  2  m 0 0 y m 1     y  0 2 0 2  1 m    1 m Do đó: 2 2 2 4 2 1 m   2m 
1 2m  m  4m 1 m 2 2  2 2 2
T  x  y        1 0 0 2  2  1 m  1 m   2 1 m 2  2 1 m 2 Phương trình: 2
x  (2  m)x 1 m  0 (m là tham số). Xét 2 2 2
  (2  m)  4( 1
  m)  4  4m  m  4  4m  m  8  0 m
 Phương trình luôn có hai nghiệm phân biệt 0.25
x  x  m  2
Áp dụng hệ thức Vi-ét, ta có: 1 2  x x  1    m 1 2
x  x  2 2   x  x 2  8   x  x 2  4x x  8 1 2 1 2 1 2 1 2 a)  m  22 2
   m   m    m  0.5 Câu 3 4( 1 ) 8 8 8 0 (1,25đ)
Vậy m  0 là giá trị cần tìm. 2 2 2 2 1 1
(x 1)  (x 1)
x  2x 1 x  2x 1 1 2 1 1 2 2 T     2 2 2 2 2 (x 1) (x 1)
(x 1) (x 1)
(x x  x  x 1) 1 2 1 2 1 2 1 2 2 2
(x  x )  2x x  2(x  x )  2 (m  2)  2( 1
  m)  2(m  2)  2 1 2 1 2 1 2   b) 2 2
(x x  x  x 1) ( 1
  m  m  2 1) 0.5 1 2 1 2 2 2
m  4m  4  2  2m  2m  4  2 m  4 4     1 2 (2) 4 4
Vậy minT  1 tại m  0 .
4x  8072  9x 18162  5 (ĐK: m  2018  )
 2 x  2018  3 x  2018  5  5 x  2018  5 a)  0.75 x  2018  1 Câu 4  x  2018  1 (1,5đ)  x  2017  (thỏa mãn ĐK)
Vậy nghiệm của phương trình là x  2017  3 3 2
x  y  3x  6x  3y  4  0 b)  2 2
x  y  3x 1 0.75
Nhờ thầy cô giải giúp nhé ! M 0.25 J O K H N
Ta có: OM  JM (JM là tiếp tuyến của (O))
NK  JM (K là trực tâm của  JMN)  OM // NK a)
Chứng minh tương tự được ON // MK 0.75
 OMKN là hình bình hành
Hình bình hành OMKN có hai đường chéo OK và MN cắt nhau tại H
 H là trung điểm của OK. Câu 5
Hình bình hành OMKN có OM = ON = a nên là hình thoi (3,5đ)
 OM = MK   OMK cân tại M  OMJ vuông tại M, có: b)  OM a 1  0 cos MOJ     MOJ  60 0.75 OJ 2a 2
  OMK là tam giác đều
 OK = OM = a  K  (O; a).
OMKN là hình thoi  MH  OK tại H
 JO là tiếp tuyến của (M; MH)  r = MH c)  OMH vuông tại H 0.75  0 a 3  a 3
MH  OM.sin MOH  a.sin 60  hay r  2 2 B I A d) a O 1.0
Giả sử IA, IB là các tiếp tuyến của (O) với A, B là các tiếp điểm * Phần thuận: Tứ giác IAOB có    0
AIB  IAO  IBO  90 nên là hình chữ nhật
Lại có OA = OB = a  IAOB là hình vuông
 OI  OA. 2  a 2  I O;a 2 * Phần đảo:
Lấy điểm I O;a 2 thì IO  a 2  OAI vuông tại A      2 2 2 2 2 IA OI OA a 2  a  a  a
Tương tự tính được IB = a  IA = IB = OA = OB = a
 Tứ giác IAOB là hình thoi  0  AIB  90
* Kết luận: Tập hợp điểm I cần tìm là đường tròn O;a 2.
Cho x, y, z là ba số thực không âm thỏa mãn: 12x 10y 15z  60 . Tìm Câu 6
T  x  y  z  x  y  0.5 (0,5đ) giá trị lớn nhất của 2 2 2 4 4 z .
Nhờ thầy cô giải giúp nhé ! Thầy Nguyễn Mạnh Tuấn
Trường THCS Cẩm Hoàng – Cẩm Giàng – Hải Dương