Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2020 – 2021 sở GD&ĐT TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP HCM
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2020-2021
MÔN THI: TOÁN CHUYÊN ĐỀ CHÍNH THỨC
Ngày thi: 17/07/2020
(Đề thi gồm 01 trang)
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Câu 1: (1,0 điểm)
Cho ba số dương a,b,c thỏa mãn điều kiện a + b + c = 2020 .
b + c c + a a + b 2 2 2  a b c 
Tính giá trị của biểu thức P =  + +
 : (a + b + c) .
 b + c c + a a + b 
Câu 2: (2,5 điểm) a) Giải phương trình 2 2
2x + x + 9 + 2x − x +1 = x + 4 . 2 2
y − 2xy = 8x − 6x +1
b) Giải hệ phương trình  . 2 3 2
y = x + 8x − x +1
Câu 3: (1,5 điểm)
Cho tam giác nhọn ABC ( AB < BC < CA) nội tiếp đường tròn (O) . Từ A kẻ đường thẳng song
song với BC cắt (O) tại A . Từ
O tại B . Từ C kẻ 1
B kẻ đường thẳng song song với AC cắt ( ) 1
đường thẳng song song với AB cắt (O) tại C . Chứng minh rằng các đường thẳng qua A , B ,C 1 1 1 1
lần lượt vuông góc với BC,C , A AB đồng quy.
Câu 4: (2,0 điểm) 2 2 2 a) Cho 2 số thực a + b (a − b)
a,b . Chứng minh rằng: ≥ ab + . 2 2 2 a + b + 2
b) Cho hai số dương a,b thỏa mãn điều kiện a + b ≤ 3 .
Tìm giá trị nhỏ nhất của biểu thức: 20 7
Q = b − a + + . a b
Câu 5: (2,0 điểm)
Đường tròn (I) nội tiếp tam giác ABC tiếp xúc với các cạnh AB, BC,CA lần lượt tại D, E, F.
Kẻ đường kính EJ của đường tròn (I) . Gọi d là đường thẳng qua A song song với BC . Đường
thẳng JD cắt d, BC lần lượt tại L, H .
a) Chứng minh: E, F, L thẳng hàng. b) J ,
A JF cắt BC lần lượt tại M , K . Chứng minh: MH = MK .
Câu 6: (1,0 điểm)
Tìm tất cả các số nguyên dương x, y thỏa mãn phương trình x 3 3 − y =1.
-------------------- HẾT --------------------
Lời giải tham khảo
Câu 1: Cho ba số dương a,b,c thỏa mãn điều kiện a + b + c = 2020 .
b + c c + a a + b 2 2 2  a b c 
Tính giá trị của biểu thức P =  + +
 : (a + b + c) .
 b + c c + a a + b  Hướng dẫn giải 2 2 2  a b c  P =  + +
 : (a + b + c)
 b + c c + a a + b    a   b   c  1 = a +  1−1 + b +1−1 + c +1−      1.   b + c   c + a   a + b
 a + b + c
 a + b + c a + b + c a + b + c  1 = . a − a + . b − b + c −  c.  b + c c + a a + b
 a + b + c  a b c (a b c)  = + + + + − (a + b +   c) 1 . 
 b + c a + c a + b 
 a + b + c
= a + b + c −1 = 2020 −1 = 2019
b + c a + c a + b
Câu 2: (2,5 điểm) a) Giải phương trình 2 2
2x + x + 9 + 2x − x +1 = x + 4 . 2 2
y − 2xy = 8x − 6x +1
b) Giải hệ phương trình  . 2 3 2
y = x + 8x − x +1 Hướng dẫn giải a. 2 2
2x + x + 9 + 2x − x +1 = x + 4
Điều kiện x∈ .  2 2 2
a = 2x + x + 9 > 0 Đặt a − b  ⇒ = x + 4 2 b = x − x + > 2 2 1 0
Khi đó phương trình trở thành 2 2 a − + = b a b
⇔ 2(a + b) = (a − b)(a + b) ⇔ a − b = 2 (do a + b > 0) 2 Do đó 2 2 2 2
2x + x + 9 − 2x − x +1 = 2 ⇔ 2x + x + 9 = 2 + 2x − x +1 2 2 2
⇔ 2x + x + 9 = 4 + 2x − x +1+ 4 2x − x +1 x ≥ 2 − 2
⇔ 2 2x − x +1 = x + 2 ⇔  2 2
4(2x − x +1) = x + 4x + 4 x ≥ 2 −  x = 0 x ≥ 2 − x = 0  ⇔  ⇔  ⇔ 2  8 7x − 8x = 0  8 x = x =  7  7 Vậy  8 S 0;  =  . 7   2 2
y − 2xy = 8x − 6x +1(1) b.  2 3 2
y = x + 8x − x +1(2)
 y − x = 3x −1  y = 4x −1
Từ phương trình (1) ta có 2 2
(y − x) = (3x −1) ⇔ ⇔   y x 1 3  − = − x  y = 1− 2x
Với y = 4x −1, thay vào (2) ta được 2 3 2 3 2 2
(4x −1) = x + 8x − x +1 ⇔ x −8x + 7x = 0 ⇔ x(x −8x + 7) = 0
x = 0 ⇒ y = 1 − x = 0  ⇔ 
⇔ x =1⇒ y = 3 2 x 8x 7 0  − + = x = 7 ⇒ y =  27
Với y =1− 2x , thay vào (2) ta được 2 3 2 3 2 2
(1− 2x) = x + 8x − x +1 ⇔ x + 4x + 3x = 0 ⇔ x(x + 4x + 3) = 0
x = 0 ⇒ y =1 x = 0  ⇔  ⇔ x = 1 − ⇒ y = 3 2 x 4x 3 0  + + = x = 3 − ⇒ y =  7 Vậy S = {(0;1),(0; 1 − ),(1;3),(7;27),( 1 − ;3),( 3 − ;7 } ) .
Câu 3: (1,5 điểm)
Cho tam giác nhọn ABC ( AB < BC < CA) nội tiếp đường tròn (O) . Từ A kẻ đường thẳng song
song với BC cắt (O) tại A . Từ B kẻ đường thẳng song song với AC cắt (O) tại B . Từ C kẻ 1 1
đường thẳng song song với AB cắt (O) tại C . Chứng minh rằng các đường thẳng qua A , B ,C 1 1 1 1
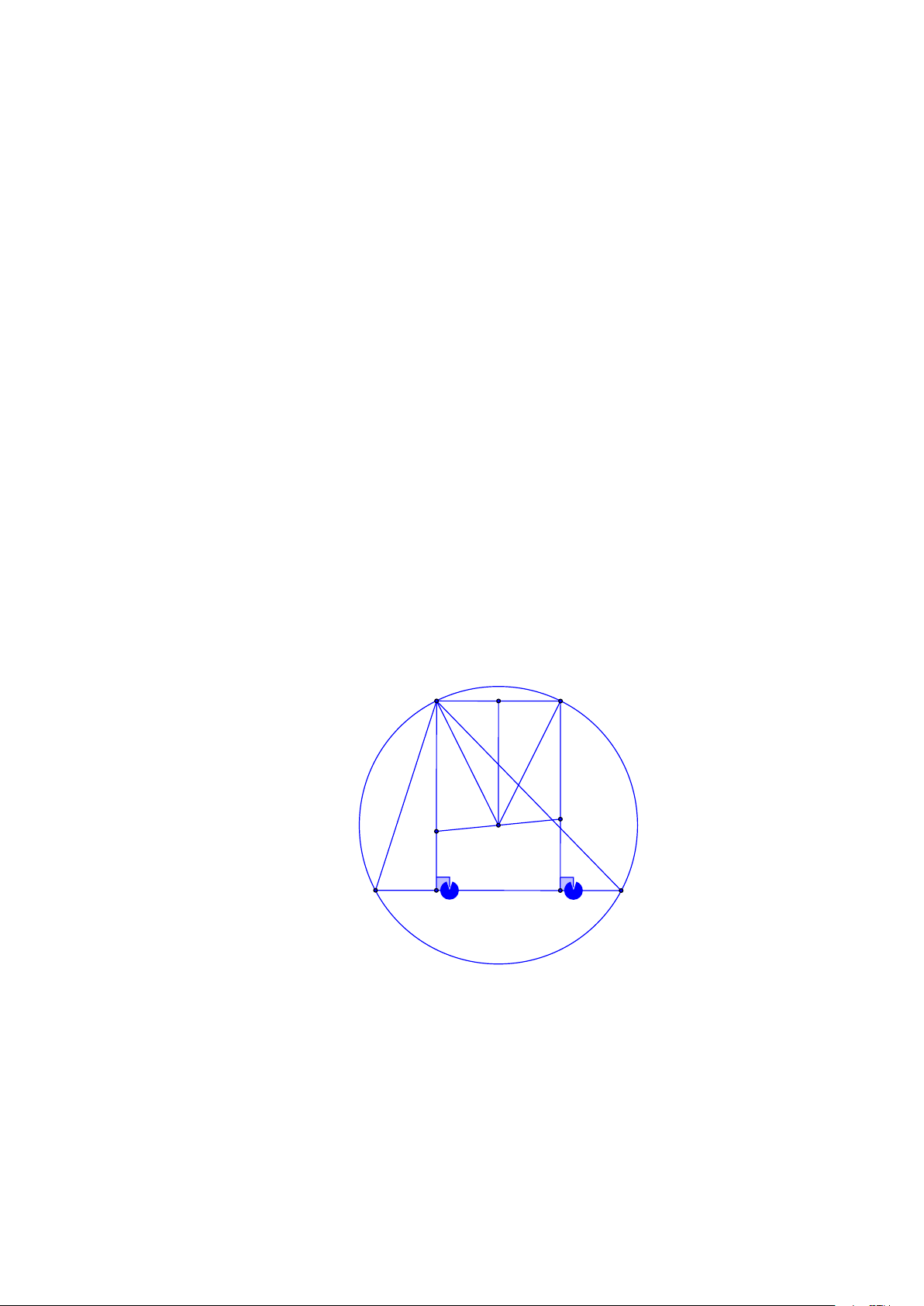
lần lượt vuông góc với BC,C , A AB đồng quy. Hướng dẫn giải A M A1 K H O B C
Gọi H là trực tâm của tam giác ABC và OH cắt đường thẳng qua A , vuông góc với BC ở 1
điểm K. Gọi M là trung điểm AA thì OM ⊥ AA . Suy ra OM ⊥ BC. 1 1
Mặt khác, tứ giác AHKA là hình thang vì AH A K nên ta có OM là đường trung bình, kéo 1  1
theo O là trung điểm HK hay nói cách khác, đường thẳng qua A , vuông góc với BC sẽ đi qua 1
điểm đối xứng với trực tâm H của tam giác ABC qua . O
Rõ ràng điểm này bình đẳng với B,C nên hai đường qua B ,C lần lượt vuông góc với C , 1 1 A AB
cũng đi qua K. Vì thế nên ta có các đường thẳng của đề bài đồng quy ở K.
Câu 4: (2,0 điểm) 2 2 2 a) Cho 2 số thực a + b (a − b)
a,b . Chứng minh rằng: ≥ ab + . 2 2 2 a + b + 2
b) Cho hai số dương a,b thỏa mãn điều kiện a + b ≤ 3 .
Tìm giá trị nhỏ nhất của biểu thức: 20 7
Q = b − a + + . a b Hướng dẫn giải 2 2 2 a) Cho 2 số thực a + b (a − b)
a,b . Chứng minh rằng: ≥ ab + . 2 2 2 a + b + 2 Ta có: a + b (a −b)2 (a −b)2 (a −b)2 2 2 ≥ ab+ ⇔ ≥ 2 2 2 2 2 a + b + 2 2 a + b + 2 (a b)2  1 1  ⇔ − − ≥   0 2 2
 2 a + b + 2  b)
Cho hai số dương a,b thỏa mãn điều kiện a + b ≤ 3
Tìm giá trị nhỏ nhất của biểu thức: 20 7
Q = b − a + + . a b
Ta có: −a ≥ b − 3 nên 20 7 20 7
Q = b − a +
+ ≥ b + b − 3+ + 20 7 = 2b − 3+ + a b 3− b b 3− b b = ( − b) 20 7 5 3 + + 7b + −18 ≥ ( −b) 20 7 2 5. 3 . + 2 7 . b −18 =16 3− b b 3− b b ⇒ Q =16 min  ( −b) 20 5 3 =  Dấu bằng xảy ra khi  3− b 
⇒ b =1 ⇒ a = 2. 7 7b =  b
Câu 5: (2,0 điểm)
Đường tròn (I) nội tiếp tam giác ABC tiếp xúc với các cạnh AB, BC,CA lần lượt tại D, E, F.
Kẻ đường kính EJ của đường tròn (I) . Gọi d là đường thẳng qua A song song với BC . Đường
thẳng JD cắt d, BC lần lượt tại L, H .
a) Chứng minh: E, F, L thẳng hàng. b) J ,
A JF cắt BC lần lượt tại M , K . Chứng minh: MH = MK . Hướng dẫn giải a)
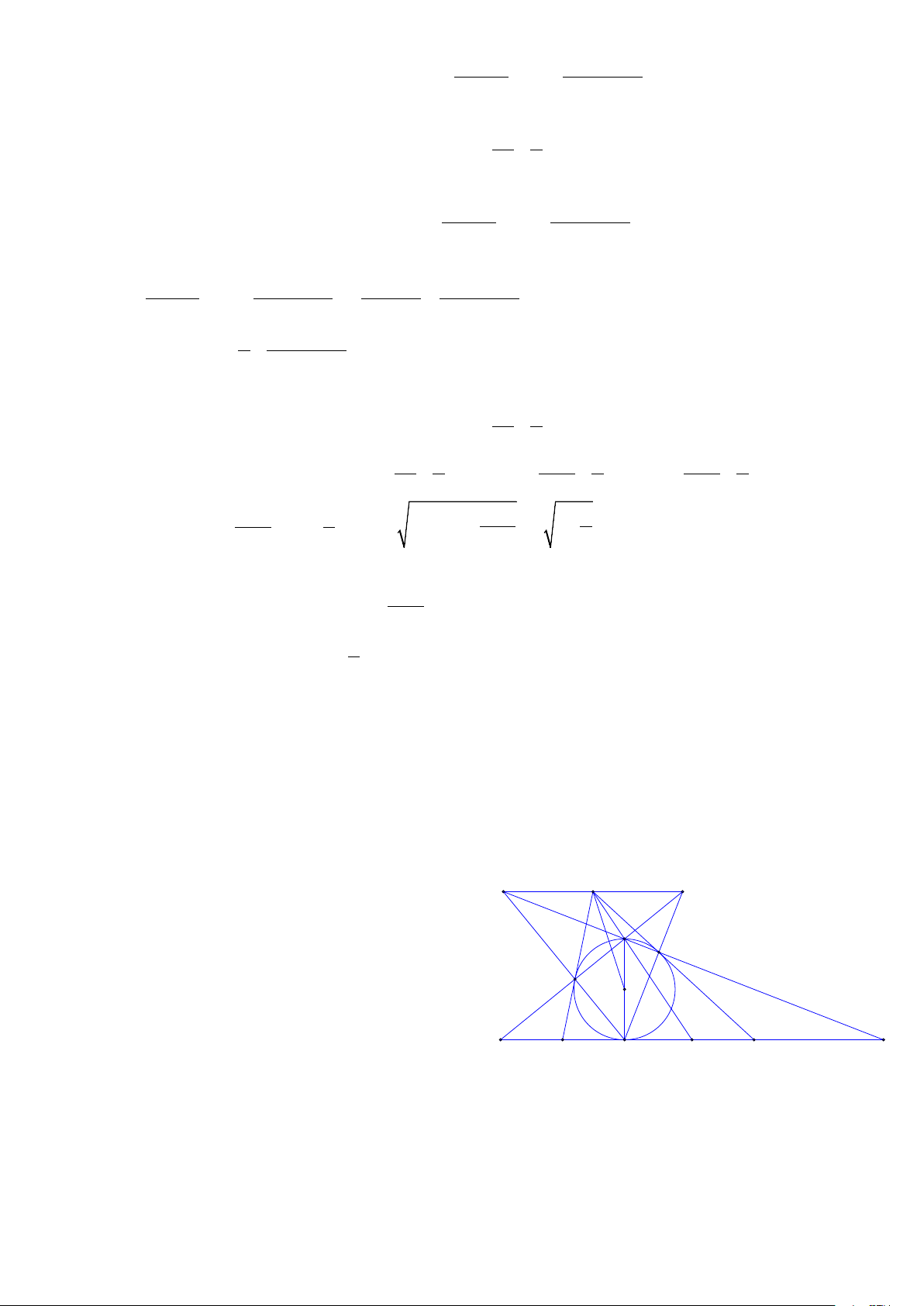
Ta có JE là đường kính của (I) nên A L T 
JDE = 90° và tam giác HDE vuông ở . D J
Chú ý rằng BD = BE , do cùng là tiếp tuyến F
kẻ từ B đến (I) nên BD = BH (tính chất D I
trung tuyến ứng với cạnh huyền).
Do đó tam giác BHD cân ở . B H K B E M C
Vì AL  BH nên hai tam giác ADL và BDH đồng dạng, kéo theo ADL cân ở A hay
AL = AD = AE.
Vì AL  CE nên  LAF = 
FCE , mà hai tam giác ALF,CEF đều cân có các góc ở đỉnh bằng nhau
nên chúng đồng dạng. Suy ra  AFL = 
CFE , kéo theo L, F, E thẳng hàng.
b) Kéo dài JF cắt d ở T thì tương tự câu a, ta có T, D, E thẳng hàng và
AT = AD = AF = A . L
Theo định lý Thales với d AL AJ AT  BC thì = =
, mà AT = AL nên MH = MK. MH JM MK
Câu 6: Tìm tất cả các số nguyên dương x, y thỏa mãn x 3 3 − y =1. Hướng dẫn giải Ta có x 3 2
3 = y +1 = (y +1)(y − y +1).Do đó, tồn tại các số tự nhiên u,v sao cho y +1= 3u  . 2
y − y +1 = 3v
Vì y +1 >1 nên 3u >1 hay u ≥1. Rút = 3u y
−1, thay vào phương trình dưới, ta có u 2
(3 −1) − (3u −1) +1 = 3v hay 2u u v 2u 1 − u v 1 3 3 3 3 3 3 3 1 3 − − ⋅ + = ⇔ − + = .
Vì vế phải nguyên nên ta phải có v −1≥ 0 hay v ≥1. Tuy nhiên, nếu v −1 > 0 thì v 1 3 − chia hết
cho 3, trong khi vế trái không chia hết cho 3, vô lý. Do đó, v =1 hay 2 2
y − y +1 = 3 ⇔ y − y = 2 .
Giải ra được y = 2. Thay vào đề bài, ta được x 3
3 = y +1 = 9 nên x = 2.
Vậy nên tất cả các nghiệm của phương trình đã cho là (x, y) = (2;2).
-------------------- HẾT --------------------
Document Outline

• BÀI GIẢI MÔN TOÁN VÀO 10 CHUYÊN TPHCM 2020