Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2021 – 2022 sở GD&ĐT Bến Tre

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 BẾN TRE
TRUNG HỌC PHỔ THÔNG CÔNG LẬP NĂM HỌC 2021 – 2022 ĐỀ CHÍNH THỨC Môn: TOÁN (chuyên)
Thời gian: 150 phút (không kể phát đề) Câu 1. (2,0 điểm)
a) Tìm tất cả các giá trị của tham số m để hàm số y  6  7m x  2 nghịch biến trên . b) Cho Parabol P 2
: y  2x và đường thẳng d  : y  x  6. Biết d  cắt P tại hai điểm phân
biệt A x ; y , B x ; y với x  x . Tính 4x  y . 2 2  1 1  1 2 2 1
c) Rút gọn biểu thức A   x   2
2 1  4x  4 x  2  7 (với x  2 ). Câu 2. (1,0 điểm) Cho phương trình: 2
x  m  3 x  4m  4  0 (1), với m là tham số. Tìm m để phương trình
(1) có hai nghiệm phân biệt x ; x thỏa x  x  x x  20 . 1 2 1 2 1 2 Câu 3. (3,0 điểm)
a) Giải phương trình nghiệm nguyên: 2 2 2
x y  xy  2x 1  y  xy  2y . 2 y  2xy  2  0
b) Giải hệ phương trình:  2 2
4x  y  y  2x  2  0.
c) Giải phương trình:  x   x   x   2 3 2 5 2 2  2x  9x 10  1 . Câu 4. (1,0 điểm)
Cho ba số thực dương x , y z thỏa 3 xy  xz  2. Chứng minh rằng: 4yz 5xz 7xy    8 . x y z Câu 5. (2,0 điểm)
Cho tam giác ABC vuông tại A với ( AB  AC ), có đường cao AH . Biết BC  1dm và 12 AH  dm . 25
a) Tính độ dài hai cạnh AB và AC
b) Kẻ HD  AB ; HE  AC (với D  AB , E  AC ). Gọi I là trung điểm của BC . Chứng minh IA  DE . Câu 6. (1,0 điểm)
Cho tam giác ABC có đường phân giác ngoài của góc A cắt đường thẳng BC tại điểm D .
Gọi M là trung điểm của BC . Đường tròn ngoại tiếp A
 DM cắt các đường thẳng AB , AC lần
lượt tại E và F (với E , F khác A). Gọi N là trung điểm của EF . Chứng minh rằng MN // AD.
____________________ HẾT ____________________ LỜI GIẢI CHI TIẾT Câu 1. (2,0 điểm)
a) Tìm tất cả các giá trị của tham số m để hàm số y  6  7m x  2 nghịch biến trên  . b) Cho Parabol P 2
: y  2x và đường thẳng d  : y  x  6. Biết d  cắt P tại hai điểm phân
biệt A x ; y , B x ; y với x  x . Tính 4x  y . 2 2  1 1  1 2 2 1
c) Rút gọn biểu thức A   x   2
2 1  4x  4 x  2  7 (với x  2 ). Lời giải 6
a) Hàm số y  6  7m x  2 nghịch biến trên   6  7m  0  m  . 7 6
Vậy m  thì hàm số đã cho nghịch biến trên . 7
b) Xét phương trình hoành độ giao điểm của P và d , ta có: 2 2
2x  x  6  2x  x  6  0 Có:    2 1  4.2.6  49  0
Vậy phương trình có 2 nghiệm phân biệt: 1 49 1 49 3 x   2  và x   1 2.2 2 2.2 2
Với x  2, ta có y  8, suy ra A2;8. 1 1 3 9  3 9 
Với x  , ta có y  , suy ra B  ; . 2  2 2 2  2 2 Khi đó, ta có: 3
4x  y  4.  8  14 . 2 1 2 Vậy 4x  y  14. 2 1 c) A   x  2  2 1  4x  4 x  2  7
 x  2  2 x  2 1 2 x  22  2.2 x  2 1
 x 1 2 x  2  2 x  2  2 1
 x 1 2 x  2  2 x  2 1
 x 1 2 x  2  2 x  2 1 do 2 x  21 0  x Vậy A  x . Câu 2. (1,0 điểm) Cho phương trình: 2
x  m  3 x  4m  4  0 (1), với m là tham số. Tìm m để phương trình
(1) có hai nghiệm phân biệt x ; x thỏa x  x  x x  20 . 1 2 1 2 1 2 Lời giải
Ta có:   m  32  4m  4  m  m   6m  6  m 10m  25  m  52 2 2 4 6 9 1 1
Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi    m  2 0
5  0  m  5  0  m  5
Vậy với m  5 thì phương trình (1) có hai nghiệm phân biệt. x  0
Theo đề bài ta có: x  x  x x  20 (2), với điều kiện 1 1 2 1 2 x  0  2
Do đó, phương trình (1) có hai nghiệm phân biệt thỏa mãn x  0 và x  0, nghĩa là 1 2 m  5 m  5   m  5
m  3  0  m  3    (*) m  1  4m  4    0 m  1 x  x  m  3
Áp dụng định lý Vi-et, ta có: 1 2  x x  4m  4  1 2 Ta có:
 x  x 2  x  x  2 x x 1 2 1 2 1 2  m  3  2 4m  4  m  3  4 m 1
 m 1 4 m 1 4   m 1 22 Từ đó, ta suy ra x  x  m 1 2 do m 1 2  0, m   1 1 2  
Từ phương trình (2), ta được
x  x  x x  20  m 1 2  4m  4  20  m 1  22  4m (3) 1 2 1 2 11
Giải phương trình (3) với điều kiện: 22  4m  0  m  (**) 2
3  m 1  22  4m2 2
 m 1  484 176m 16m 2  16m 177m  485  0 4 Ta có:    1
 772  4.16.485  289  0
Vậy phương trình (4) có 2 nghiệm phân biệt: 177  289 177  289 97 m   5 và m   2.16 2.16 16
So với điều kiện (*) và (**) thì m  .
Vậy không tồn tại giá trị của m thỏa mãn yêu cầu bài toán. Câu 3. (3,0 điểm)
a) Giải phương trình nghiệm nguyên: 2 2 2
x y  xy  2x 1  y  xy  2y . 2 y  2xy  2  0
b) Giải hệ phương trình:  2 2
4x  y  y  2x  2  0.
c) Giải phương trình:  x   x   x   2 3 2 5 2 2  2x  9x 10  1 . Lời giải a) Ta có: 2 2 2
x y  xy  2x 1  y  xy  2y 2 2 2
 x y  xy  2x 1 y  xy  2y  0   2 2 x y  xy    2
xy  y   2 x  y  1
 xy  x  y  y x  y  2 x  y  1
  x  yxy  y  2 1   1
Vì đây là phương trình nghiệm nguyên nên ta có: x  y 1  (*)       xy y 2 1 1   x  y  1    ** xy  y  2  1  x  1 y         x 1 y x 1 y  x  0; y  1 *       y   1 y   1 2 y  y 1  0   y 1  0  x  2; y  1  y  1  x  1 y x  1 y x  1 y  x  2  ; y  1 ( * * )       y    1 y   1 2 y  y  3  0  y  2y  3  0  x  2; y  3  y  3 
Vậy tập nghiệm của hệ phương trình là: S  
 0; 1,2; 1,2; 1,2; 3  . b) Ta có: 2 2 y  2xy  2  0 y  2xy  2    2 2
4x  y  y  2x  2  0  2 2  4x  y 
 y  2x  2y  2xy  0 2 y  2xy  2  2x y 
2x  y 2x  y  y2x  y  0 2 y  2xy  2    2x  y 
2x  y 1 y  0 2 y  2xy  2  2x y  2x   1  0 2 y  2xy  2   2x  y  0  2x 1  0 Mặt khác, 2
y  2xy  2  y  y  2x  2, nghĩa là y  2x  0 .
Do đó, từ hệ phương trình ban đầu đề cho, ta giải hệ phương trình sau:  1  1 x  2  y  2xy  2 x    2    2      y  1 2x 1 0 2
y  y  2  0  y  2 1   1 
Vậy hệ có tập nghiệm là S   ;1, ;2   2   2 
c) Giải phương trình (*):  x   x   x   2 3 2 5 2 2  2x  9x 10  1 .  5   2x  5  0 x  2  
Điều kiện xác định: x  2  0  x  2   x  2 .  2  2x  9x 10  0 5  x   x  2  2
a  2x  5 a   1 Ta đặt  b   x  2 b  0 2 2
a  2b  2x  5  2x  2  1  Ta thấy 2 2
a  b  2x  5  x  2  x  3 
ab  2x  5 x  2 2  2x  9x 10
Phương trình (*) trở thành:  2 2 a  b a  2b 2 2  ab  a  2b   2 2
a  b a  2b   2 2 a  b    2 b  ab  0   2 2 a  b a  2b   1   2 b  ab  0
 a  ba  ba  2b   1  ba  b  0
 a  ba  ba  2b   1  b  0 a  b  0   1
 aba2b 1b 0 2
Vì a  b  1 nên ta chỉ giải phương trình (2)
a  ba  2b  
1  b  0  a  ba  b  
1  ba  b  b  0
 a  ba  b   1  ba  b   1  0       a  b  a  b a b 1 0 1 2  0  a2b  0
TH1: Với a  2b  0 , ta có
a  2b  0  2x  5  2 x  2  0  2x  5  2 x  2  x    x   3 2 5 4 2  x   2 3
So với điều kiện thì x   (Nhận). 2
TH2: Với a  b 1  0 , ta có
a  b 1  0  2x  5  x  2 1  0  2x  5  x  2 1
 2x  5  x  3  2 x  2
 x  2  2 x  2  0
 x  2 x  2  2  0  x  2  0 x  2  0 x  2  x  2           x  2  2  0  x  2  2 x  2  4 x  2
So với điều kiện thì x  2 (Nhận) và x  2  (Nhận). 3
Vậy tập nghiệm của phương trình là S  2; ;  2 . 2 Câu 4. (1,0 điểm)
Cho ba số thực dương x , y z thỏa 3 xy  xz  2. Chứng minh rằng: 4yz 5xz 7xy    8 . x y z Lời giải 4yz 5xz 7xy Ta đặt M    , ta có x y z 4yz 5xz 7xy M    x y z yz yz xz xz xy xy   3   4  3  4 x x y y z z  yz xz   yz xy   xz xy     3       4   x y  x z   y z    
Áp dụng bất đẳng thức Cauchy, ta được yz xz yz xy xz xy M  2 .  3.2 .  4.2 . x y x z y z  2z  6y  8x
 2z  2x  6y  6x
Tiếp tục áp dụng bất đẳng thức Cauchy, ta được M  2.2 xz  6.2 xy
 4 xz  3 xy  4.2  8 x  y  z  1
Dấu “  ” xảy ra khi và chỉ khi   x  y  z  .  xz  3 xy  2 2  1
Vậy khi x  y  z  thì M  8 (đpcm). 2 Câu 5. (2,0 điểm)
Cho tam giác ABC vuông tại A với ( AB  AC ), có đường cao AH . Biết BC  1dm và 12 AH  dm . 25
a) Tính độ dài hai cạnh AB và AC
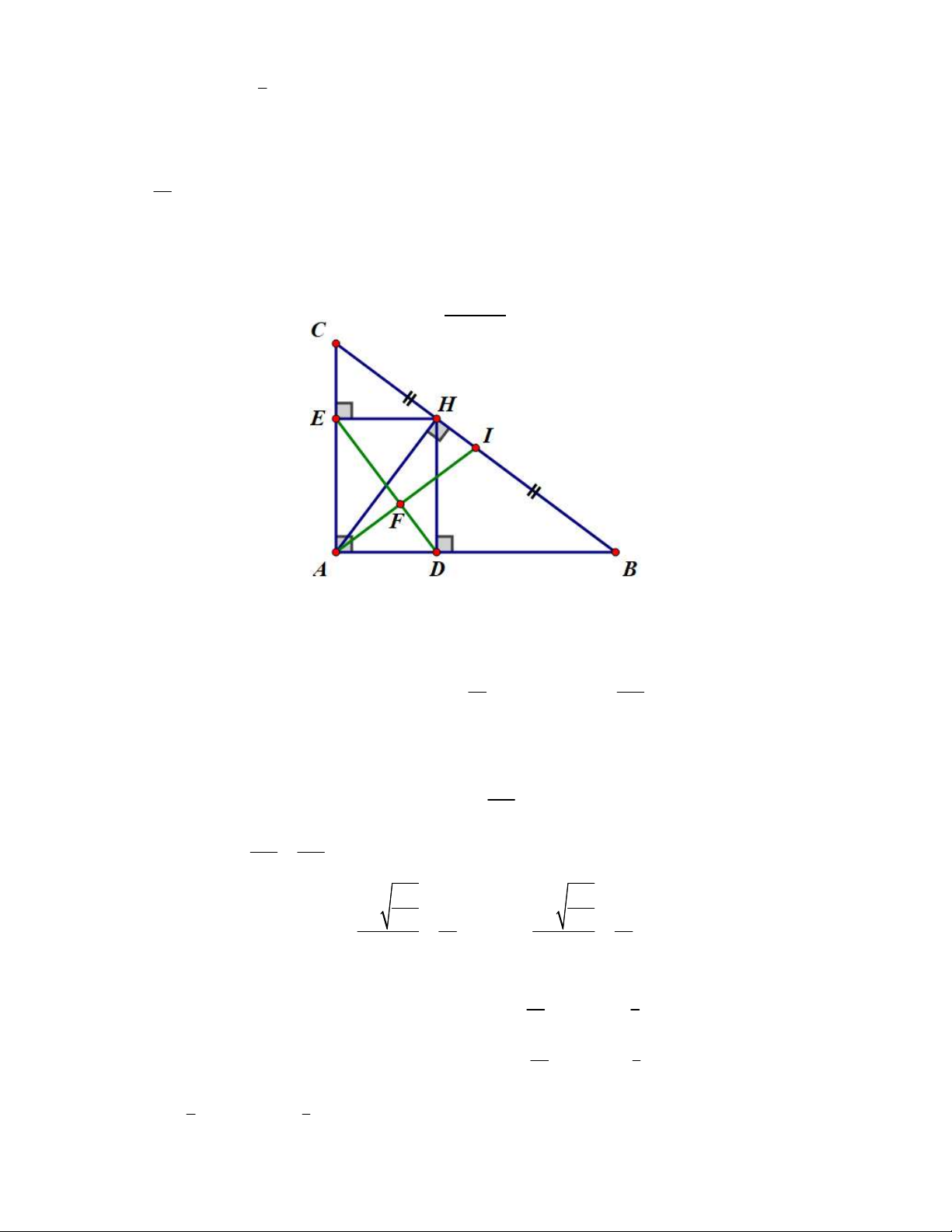
b) Kẻ HD  AB ; HE  AC (với D  AB , E  AC ). Gọi I là trung điểm của BC . Chứng minh IA  DE . Lời giải
a) Tính độ dài hai cạnh AB và AC
Áp dụng hệ thức lượng và định lý Pytago cho A
 BC vuông tại A, ta có: 2 2 2 2 2 AB  AC  BC  1 AB  AC 1    12   2 2 144 A . B AC  AH.BC  AB .AC     25  625 Khi đó, 2 AB và 2
AC là các nghiệm dương của phương trình.
Áp dụng hệ quả của định lý Vi-et, ta được 2 144 X 1X   0 625 Ta có: 2 144 49   1  4.1. 
 0 nên phương trình trên có 2 nghiệm phân biệt: 625 6 5 2 49 49 1 1 625 9 625 16 X   và X   1 2.1 25 2 2 25
Theo giả thiết, AB  AC , nên ta được:  2 16  4 AB  X  AB   1    2 2 25 5 AB  AC     2 9 3 AC  X   AC  2  25  5 4 3
Vậy AB  dm và AC  dm . 5 5 b) Chứng minh IA  DE .
Gọi F là giao điểm của AI và DE .   HEA  90 HE  AC   
Xét tứ giác EHDA , ta có:   HDA  90 HD  AB    DA E  90   ABC vuoâng taïi A
 Tứ giác EHDA là hình chữ nhật (tứ giác có 3 góc vuông)
 Tứ giác EHDA là tứ giác nội tiếp.   ADE  
AHE (hai góc nội tiếp cùng chắn cung AE ) Mà  AHE   ECH (cùng phụ với  CHE )   ADE   ECH   ADE   ACB (1) Xét A
 BC vuông tại A có I là trung điểm của BC 1
 IA  IB  BC (định lý đường trung tuyến trong tam giác vuông) 2  I  AB cân tại I   IAB   IBA (2)
Từ (1) và (2), ta suy ra:  ADE  IAB  ACB  IBA  ACB  ABC 90       ( A  BC vuông tại A)
Áp dụng định lý tổng 3 góc trong ADF , ta có:        
FAD  FDA  AFD  180  AFD  180  FAD  FDA     
 A FD  180  IAB  ACB     
 AFD  180  ABC  ACB     
 A FD  180  90  90 ABC vuoâng taïi A Do đó, IA  DE (đpcm) Câu 6. (1,0 điểm)
Cho tam giác ABC có đường phân giác ngoài của góc A cắt đường thẳng BC tại điểm D .
Gọi M là trung điểm của BC . Đường tròn ngoại tiếp A
 DM cắt các đường thẳng AB , AC lần
lượt tại E và F (với E , F khác A). Gọi N là trung điểm của EF . Chứng minh rằng MN // AD. Lời giải
Dựng hình bình hành BPCF .
 Hai đường chéo BC và PF cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC (gt)  M cũng là trung điểm của PF .
Xét PEF , ta có N là trung điểm của EF (gt), M là trung điểm của PF (cmt)
 MN là đường trung bình của PEF  MN  EP (1) Ta có:  MPB  
MFA (cặp góc so le trong của PB  FA , PBFC là hình bình hành) Mà  MDA   MEA  
MFA (các góc nội tiếp cùng chắn cung AM )   MEA   MPB , nghĩa là  MEB   MPB
Xét tứ giác BMEP , ta có  MEB   MPB (cmt)
 Tứ giác BMEP nội tiếp (tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau)   BEP  
BMP (hai góc nội tiếp cùng chắn cung BP ) Mà  BMP   FMD (đối đỉnh) Mặt khác  FMD  
FAD (hai góc nội tiếp cùng chắn cung FD )   BEP   FAD , nghĩa là  AEP   FAD (2)
Ta có: AD là phân giác ngoài của  BAC (gt) Mà  BAC  CAE 180   (kề bù)
 AD là phân giác của  CAE   FAD   EAD (3)
Từ (2) và (3), ta suy ra  AEP   EAD
Mà 2 góc nằm ở vị trí so le trong nên EP  AD (4)
Từ (1) và (4), ta suy ra MN  AD (đpcm).
__________ THCS.TOANMATH.com __________