Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2021 – 2022 sở GD&ĐT Bình Phước

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM 2021 BÌNH PHƯỚC MÔN THI: TOÁN CHUYÊN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 9/6/2021
(Đề thi gồm có 01 trang)      2    1 1 x 2 x x x x x 1
Câu 1. (1,5 điểm) Cho biểu thức A   :      x  x x  x   x 1      a) Rút gọn biểu thức . A
b) Tìm x nguyên để A nhận giá trị nguyên. Câu 2. (2,0 điểm) a) Giải phương trình: 2
2x 2x  3  3x  6x  1  2 x  xy  x  y    x   2 2 4 3 4 4 9 1 x  2xy  x  2 y
b) Giải hệ phương trình: 
 x 1  x  2y  2x  2y  5 
Câu 3. (1,5 điểm) Cho phương trình: 2 2
x  2(m  3)x  3m  8m  5  0 , với m là tham số.
a) Tìm m để phương trình có 2 nghiệm trái dấu.
b) Tìm m để phương trình có 2 nghiệm x ; x phân biệt thỏa mãn điều kiện: 1 2 2 2
x  2x  3x x  x  x . 1 2 1 2 1 2
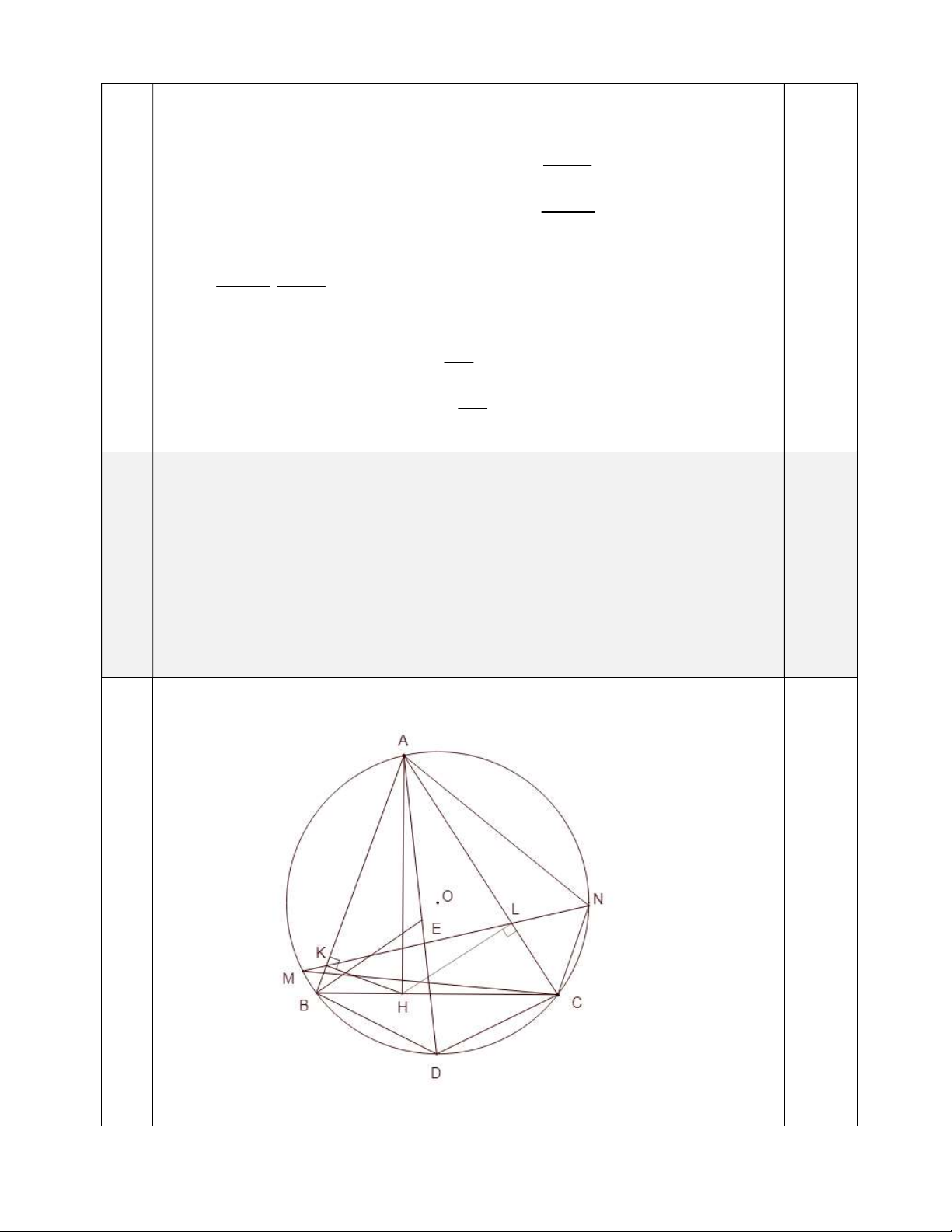
Câu 4. (3,0 điểm) Cho tam giác nhọn ABC  AB  AC nội tiếp đường tròn O , D là
điểm chính giữa trên cung nhỏ BC của đường tròn O, H là chân đường cao kẻ từ A
của tam giác ABC. Hai điểm K , L lần lượt là hình chiếu vuông góc của H lên AB và AC. a) Chứng minh A . L CB  A . B K . L
b) Lấy điểm E trên đoạn thẳng AD sao cho BD  DE . Chứng minh E là tâm
đường tròn nội tiếp tam giác ABC.
c) Đường thẳng KL cắt đường tròn O tại hai điểm M , N ( K nằm giữa M , L ).
Chứng minh AM  AN  AH. Câu 5. (1,0 điểm)
a) Tìm nghiệm nguyên của phương trình: 2x  yx  y  32x  y  5x  y  22.
b) Cho hai số tự nhiên a, b thỏa mãn 2 2 2a  a  3b  . b Chứng minh rằng
2a  2b 1là số chính phương.
Câu 6. (1,0 điểm) Cho a, b, c là các số dương. Chứng minh rằng: 3 a b a)  a  . 2 2 a  b 2 3 3 3 a b c a  b  c b)    . 2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 3 ............HẾT...........
Thí sinh không được sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm. 0
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KỲ THI TUYỂN SINH BÌNH PHƯỚC LỚP 10 NĂM 2021
(Hướng dẫn chấm gồm 07 trang) MÔN THI: TOÁN CHUYÊN
Lưu ý: - Điểm toàn bài lấy điểm lẻ đến 0,125.
- Học sinh giải cách khác với đáp án thì giám khảo xem xét, nếu đúng vẫn cho điểm tối đa. Câu Nội dung Điểm      2 x  2 x   x x x x 1 1 1 1 Cho biểu thức A   :     .  1,5 x  x x  x   x 1     
a) Rút gọn biểu thức A. 1,0 0,25 ĐKXĐ: x  0, x  1  x  1x x x x   1 1 x  x 1 Ta có   x  x x  x   1 x  x  1x x x x   1 1 x  x 1   0,5 x  x x  x   1 x x x    x  2 2 2 1 2 1 2 x   1   x 1  x  1 x  1 x 1        2   1 1  x x x x x  1  Vậy x 1 A   :       0,25 x x   x 1  x 1    
b) Tìm x nguyên để A nhận giá trị nguyên 0,5  Ta có x 1 2 A   1 0,125 x 1 x 1
Để A nhận giá trị nguyên thì x 1 là ước của 2 . Hay  x   1 2;2;1;  1 .
 x 1  2  x  1  l  0,25
 x 1  1  x  0  x  0 l Suy ra 
 x 1  2  x  3  x  9n 
 x 1  1  x  2  x  4  n
Vậy có 2 giá trị x  4; x  9 thì A nguyên. 0,125 2 a) Giải phương trình: 2
2x 2x  3  3x  6x  1. 2,0 1
b) Giải hệ phương trình:  2 x  xy  x  y    x   2 2 4 3 4 4 9 1 x  2xy  x  2 y 
 x 1  x  2y  2x  2y  5.  a) Giải phương trình: 2
2x 2x  3  3x  6x  1. 1,0 ĐKXĐ: 3 x  0,125 2 Ta có 2 Pt  x  x   x
x   x  x   x  x     x  2 2 2 2 3 2 2 3 4 8 4 2 3 2 2 0,25 x  2x  3  2x  2  2x  3  x  2    
x  2x  3  2x  2  2x  3  3  x  2 x  2 x  2  x  1  (n)  2 x  2x 1  0  2 0,5  x     2    3 x     3 x  1  (n)   2 9  x 10x 1  0  1 x   (l)  9
Kết hợp với điều kiện phương trình có nghiệm là x  1 . 0,125
b) Giải hệ phương trình:  2
 x  xy  x  y   x   2 2 4 3 4 4 9 1 x  2xy  x  2 y  1,0
 x 1  x  2y  2x  2y  5.    x   2
1 x  2xy  x  2y  0   Điều kiện: x 1  0  0,125 x  2y  0  2x  2y  5  0 Ta có phương trình (2)  x 1 2  x  
1  x  2y  x  2y  2 x  y  5  0,25 2  x  
1  x  2y  4   x   1  x  2y  2  x   1  x  2y 2
 4  x  2xy  x  2y  4 (*) Ta có phương trình (1)   2
x  xy  x  y  x   x   2 2 2 2 4 9 1 x  2xy  x  2y 0,25
 8  x  4  36x   1  36 x   1  x  4 2 x  4  x  4  x  4        x  2 (n) 3  6   x   2 1  x  8x 16 2 x  28x  52  0 x   26 (n)
 Với x  2 thay vào (*) ta có: 1
pt (*)  4  4y  2  2y  4  6  y  2   y  (thỏa mãn). 3  0,25
Với x  26 thay vào (*) ta có: 349
(*)  676  52y  26  2 y  4  54y  6  98  y  .(thỏa mãn). 27 x  2 x  26  
Kết luận: Hệ có 2 nghiệm là:  1 và  349 . 0,125 y   y   3  27 Cho phương trình: 2 2
x  2(m  3)x  3m  8m  5  0 , với m là tham số.
a) Tìm m để phương trình có 2 nghiệm trái dấu. 3
b) Tìm m để phương trình có 2 nghiệm x ; x phân biệt thỏa mãn điều 1,5 1 2 kiện 2 2 x  2x  3x x  x  x 1 2 1 2 1 2
a) Tìm m để phương trình có 2 nghiệm trái dấu. 0,75
Để phương trình có 2 nghiệm trái dấu thì 2
x .x  0  3m  8m  5  0  m 1 3m  5  0 0,25 1 2    m 1 m 1  0  5   m  3  m  5  0   3 5    1 m    0,375 m 1  0 m 1 3      3  m  5  0  5  m    3 Vậy 5
1  m  thì thỏa yêu cầu bài toán. 0,125 3
b) Tìm m để phương trình có 2 nghiệm x ; x phân biệt thỏa mãn điều 1 2 kiện 2 2 x  2x  3x x  x  x 0,75 1 2 1 2 1 2
Phương trình có 2 nghiệm phân biệt thì   m  32 2 2 2            3m 8m 5 0 m 6m 9 3m 8m 5 0 0,125 2
 2m  2m  4  0  1  m  2 x  x  2(m  3) (1)
Theo định lý Vi-et ta có: 1 2  0,125 2 x x  3m  8m  5 (2)  1 2 Theo đề ta có x  x  0 2 2
x  2x  3x x  x  x  x  x x  2x  x  x  1 2 1 2 1 2  1 2  1 2  1 2 1 2  0,25 x  2x 1  0  1 2 3
 TH1: x  x  0 (loại vì x  x ). 1 2 1 2  TH2: x  2x 1  0 , kết hợp với (1) ta có hệ: 1 2  2m  7 
x  x  2m 3 x     2 3x 2m 7 1 2 2  3      x  2x 1  0 x  2x 1 4m 11  1 2  1 2 x  1  3
Thay x ; x tìm được vào (2) ta có: 1 2 4m 11 2m  7 0,25 2 .  3m  8m  5 3 3 m  2 l 2 19m 22m 32 0       16 m  tm  19 
Kết hợp với điều kiện ta có 16 m 
thì thỏa yêu cầu bài toán. 19
Cho tam giác nhọn ABC  AB  AC  nội tiếp đường tròn O , D là điểm chính
giữa trên cung nhỏ BC của đường tròn O, H là chân đường cao vẽ từ A của
tam giác ABC. Hai điểm K, L lần lượt là hình chiếu vuông góc của H lên AB và AC . 4 a) Chứng minh A . L CB  A . B KL . 3,0
b) Lấy điểm E trên đoạn thẳng AD sao cho BD  DE . Chứng minh E là
tâm đường tròn nội tiếp tam giác ABC.
c) Đường thẳng KL cắt đường tròn O tại hai điểm M , N ( K nằm giữa
M , L ). Chứng minh AM  AN  AH. 4 a) Chứng minh A . L CB  A . B KL . 1
Xét hai tam giác AKL và ACB , có: + A chung + AK AL 2 AK.AB  AH  A . L AC   . 0,5 AC AB
Suy ra hai tam giác AKL và ACB đồng dạng. Suy ra AL KL   A . L CB  A . B K . L AB CB 0,5
b) Lấy điểm E trên đoạn thẳng AD sao cho BD  DE . Chứng minh E
là tâm đường tròn nội tiếp tam giác ABC. 1,0
Ta có D là điểm chính giữa trên cung nhỏ BC nên AE là đường phân giác trong 0,25
của góc A của tam giác ABC. (*)
+ Tam giác DBE cân tại D nên :  BED   EBD   1 . 0,125 +  BED   BAD   ABE   BCD   ABE   DBC   ABE 2 . 0,25 + Ta có  EBD   DBC   EBC 3 0,125 Từ (1), (2), (3) suy ra  ABE  
EBC hay BE là phân giác trong của góc B của tam giác ABC *  * . 0,25
Từ (*) và (**) suy ra E là tâm đường tròn nội tiếp tam giác ABC.
c) Đường thẳng KL cắt đường tròn O tại hai điểm M , N ( K nằm giữa 1,0
M , L ). Chứng minh AM  AN  AH.
+ Hai tam giác AKL và ACB đồng dạng. Suy ra  ALK   1 ABC  s  AM  sd   NC  1 d  sd  AC 2 2 1  0.5 sd  AM  sd   NC  1  sd  AN  sd   NC  2 2  sd  AM  sd  AN  AN  AM 4
+ Chứng minh được hai tam giác ALN và ANC đồng dạng vì có góc A chung và  ANL  
ACN (cùng chắn 2 cung bằng nhau). 0,5 Suy ra AL AN 2   AN  A . L AC. Mà 2 A .
L AC  AH  AN  AH 5 AN AC
Từ (4) và (5) ta suy ra AM  AN  AH.
a) Tìm nghiệm nguyên của phương trình:
2x  yx  y  32x  y5x  y  22 1,0 5
b) Cho hai số tự nhiên a,b thỏa mãn 2 2 2a  a  3b  . b Chứng minh rằng
2a  2b 1 là số chính phương.
a) Tìm nghiệm nguyên của phương trình: 0,5 5
2x  yx  y  32x  y5x  y  22
Ta có 2x  y x  y  32x  y  5 x  y  22
 2x  yx  y  3 5x  y  3  7 0,125
 2x  y  5x  y  3  7
Vì 7 1.7  7.1    1 . 7
   7. 
1 nên ta có 4 trường hợp xảy ra. 0,125  10 x  2x  y  5  1  TH1:  3    (loại). x  y  3  7 2  y   3 0,125  10 x  2x  y  5  7  TH2:  3    (loại). x  y  3  1 16  y   3 2x  y  5  1  x  2  TH3:    (thỏa mãn) x  y  3  7  y  8 2x  y  5  7  x  2  TH4: 0,125    (thỏa mãn) x  y  3  1  y  2
Vậy phương trình đã cho có hai nghiệm  ; x y là  2  ;8 và  2  ;2
b) Cho hai số tự nhiên a,b thỏa mãn 2 2 2a  a  3b  . b Chứng minh rằng 0,5
2a  2b 1 là số chính phương. Ta có 2 2
a  a  b  b  a  b a  b   2 2 3 2 2 1  b *
Gọi d  a  b, 2a  2b   1 với * d     a  b  d 0,25 Suy ra 
 a  b2a  2b   2   2 2  b d  bd.  a  b    1 d 2 2 1 d
Vì a  bd  ad  2a  2bd mà 2a  2b   1 d nên 1d  d  1 0,125
Do đó a  b,2a  2b  
1  1. Từ (*) ta được a  b và 2a  2b 1 là số chính
phương. Vậy 2a  2b 1 là số chính phương. 0,125
Cho a,b,c là các số dương. Chứng minh rằng: 3 a b a)  a  . 1,0 6 2 2 a  b 2 3 3 3 a b c a  b  c b)    . 2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 3 3 a b a)  a  . 0,5 2 2 a  b 2 a a  2 2 a  b  2 3 2  ab ab Ta có   a  . 2 2 2 2 2 2 0,25 a  b a  b a  b 6 2 2 ab ab b Theo BĐT Cauchy ta có a   a   a  . 2 2 a  b 2ab 2 0,25 3 3 3 a b c a  b  c b)    . 0,5 2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 3 3 b c 3 c a
Tương tự theo câu a) ta có :  b  ,  c  . 2 2 b  c 2 2 2 c  a 2
Cộng vế theo vế ba bất đẳng thức trên ta có: 0,125 3 3 3 a b c a  b  c    . 2 2 2 2 2 2 a  b b  c c  a 2 3 3 3 a a 2 a Ta có:   . . 2 2 2 2 2 2 a  ab  b   0,125 2 a b 2 3 a b a   b 2 3 3 b 2 b 3 3 c 2 c Tương tự ta có  . ,  . . 2 2 2 2 b  bc  c 3 b  c 2 2 2 2 c  ca  a 3 c  a 0,125
Cộng vế theo vế ba bất đẳng thức trên ta có: 3 3 3 a b c   2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 3 3 3 2  a b c  a  b  c 0,125       . 2 2 2 2 2 2 3  a  b b  c c  a  3 HẾT. 7