Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2021 – 2022 sở GD&ĐT Quảng Bình

SỞ GD&ĐT QUẢNG BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2021 - 2022 ĐỀ CHÍNH THỨC Khóa ngày 08/6/2021 Môn: TOÁN (CHUYÊN)
SBD:………….. Thời gian làm bài: 150 phút (không kể thời gian giao đề)
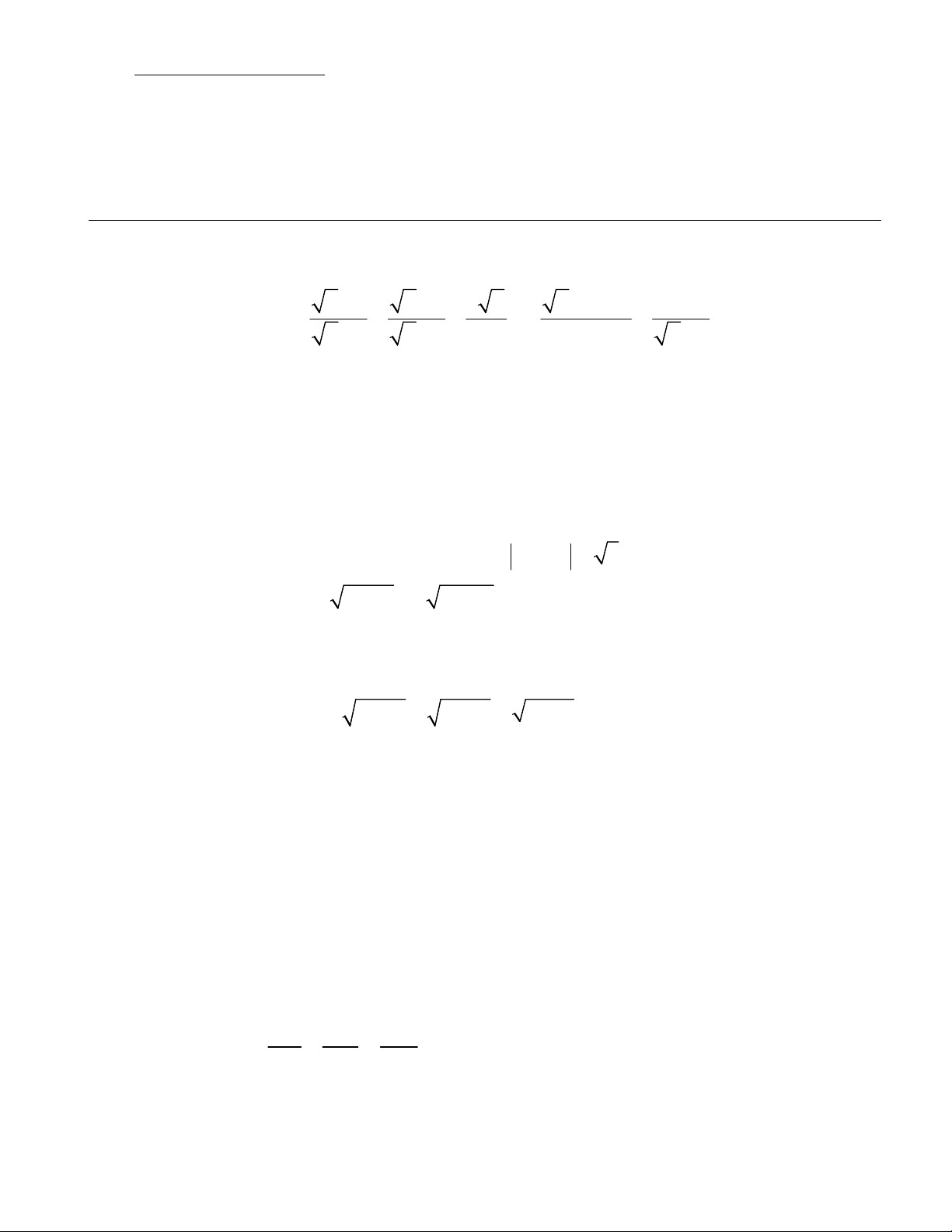
Đề có 01 trang gồm 5 câu Câu 1 (2,0 điểm).  x 1
x 1 8 x   x  x  3 1  Cho biểu thức P     :   (với x  0, x  1). x 1 x 1 x 1 x 1 x 1     a) Rút gọn biểu thức . P
b) Tìm tất cả các số thực x để P nhận giá trị nguyên. Câu 2 (2,0 điểm).
a) Trong mặt phẳng tọa độ Oxy, cho parabol P 2
: y  x và đường thẳng
d : y  2mx  m 1 (với m là tham số). Tìm tất cả các giá trị của m để d cắt P tại
hai điểm phân biệt có hoành độ x , x thỏa mãn x  x  3. 1 2 1 2
b) Giải phương trình 8 5x 1  6 2x  3  7x  29. Câu 3 (1,0 điểm).
Cho ba số thực x, y, z 5;7. Chứng minh rằng
xy  1  yz 1  zx  1  x  y  z. Câu 4 (1,5 điểm).
Tìm tất cả các số nguyên dương n sao cho hai số 2 n  2n  7 và 2 n  2n 12 đều là
lập phương của hai số nguyên dương nào đó. Câu 5 (3,5 điểm).
Cho tam giác nhọn ABC nội tiếp đường tròn O đường kính AE. Gọi D là một điểm bất kì trên cung 
BE không chứa điểm A ( D khác B và E ). Gọi H , I, K lần lượt là hình
chiếu vuông góc của D lên các đường thẳng BC, CA và A . B
a) Chứng minh ba điểm H , I, K thẳng hàng. AC AB BC b) Chứng minh    DI DK DH
c) Gọi P là trực tâm của A
 BC, chứng minh đường thẳng HK đi qua trung điểm của đoạn thẳng D . P
...........................Hết......................... SỞ GD&ĐT QUẢNG BÌNH HƯỚNG DẪN CHẤM
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2021 - 2022 Khóa ngày 08/6/2021 Môn: TOÁN (CHUYÊN)
(Hướng dẫn chấm gồm có 05 trang) Yêu cầu chung
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu phải
lập luận logic chặt chẽ, đầy đủ, chi tiết rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với những bước sau có liên quan.
* Điểm thành phần của mỗi câu được phân chia đến 0,25 điểm. Đối với điểm là 0,5 điểm
thì tùy tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Đối với Câu 5, học sinh không vẽ hình thì cho điểm 0. Trường hợp học sinh có vẽ hình,
nếu vẽ sai ở ý nào thì điểm 0 ở ý đó.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tùy theo mức điểm từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm  x 1
x 1 8 x   x  x  3 1  Cho biểu thức P     :   x 1 x 1 x 1 x 1 x 1     1 (với x  0, x  1). 2,0 điểm a) Rút gọn biểu thức . P
b) Tìm tất cả các số thực x để P nhận giá trị nguyên.
 x  2  x  2 1 1  8 x
x  x  3   x   1 Ta có: P   0,5 x   x   : 1 1  x  1 x  1  x  1 x x   1 4 4 x a     x   1  x   . 1 x  4 x  4 0,5 4 x Vậy P  . x  4 4 x b
Vì x  0, x  1 nên P   0. 0,25 x  4 HDC TOÁN CHUYÊN trang 1/5 Câu Nội dung Điểm  x x x x    2 2 4 4 4 Ta có: 1 P 1    0 suy ra P 1. 0,25 x  4 x  4 x  4
Do đó 0  P 1 mà 𝑃 ∈ 𝑍 nên P  0 hoặc P  1. 0,25
Với P  0 thì x  0 (thỏa mãn).
Với P  1 thì x  2  0  x  4 (thỏa mãn). 0,25
Vậy x  0; x  4 thì P nhận giá trị nguyên.
a) Trong mặt phẳng tọa độ Oxy , cho parabol P 2 : y  x và đường
thẳng d  : y  2mx  m 1 (với m là tham số). Tìm tất cả các giá trị 2
của m để d  cắt P tại hai điểm phân biệt có hoành độ x , x thỏa 1 2 2,0 điểm mãn x  x  3. 1 2
b) Giải phương trình: 8 5x 1  6 2x  3  7x  29.
Xét phương trình hoành độ giao điểm của d  và P : 2 2
x  2mx  m 1  x  2mx  m 1  0  1 2  1  3 Ta thấy 2
'  m  m 1  m    0   , với mọi m  .  0,25  2  4 Suy ra phương trình  
1 có hai nghiệm phân biệt với mọi m . 
Do đó đường thẳng d  cắt P tại hai điểm phân biệt với mọi m . 
Ta có x , x là hai nghiệm của phương trình   1 1 2 a x  x  2m 0,25
Áp dụng định lí Vi-ét ta được 1 2  x  x  m 1  1 2 Ta có 2 2 x  x  3  x  x  3  x  x  4x x  3  0. 0,25 1 2  1 2  1 2 1 2
 4m  4m 1 0  2m  2 1 2 1  0  m  . 2 1
Vậy m  thì d  và P cắt nhau tại hai điểm phân biệt có hoành độ 0,25 2
x ; x thỏa mãn x  x  3. 1 2 1 2 1 Điều kiện: x   . 5 0,5 b
Ta có: 8 5x 1  6 2x  3  7x  29.
 5x 18 5x 1 16  2x  3 6 2x  3  9  0 HDC TOÁN CHUYÊN trang 2/5 Câu Nội dung Điểm
  x   2   x   2 5 1 4 2 3 3  0  5x 1  4  0    x  3 (thỏa mãn). 0,5  2x  3  3  0
Vậy phương trình có nghiệm x  3.
Cho ba số thực x, y, z 5;7. Chứng minh rằng 3 1,0 điểm
xy  1  yz 1  zx  1  x  y  z. Do x y 
 x  y   x  y2 , 5;7 2  4 0,25
 x  xy  y   x  y2 2 2 2 4  4xy   1  x  y  2 xy 1
Chứng minh tương tự ta có: 0,25
y  z  2 yz 1; z  x  2 zx 1
Cộng vế theo vế các bất đẳng thức trên, ta có
2 x  y  z  2 xy 1  yz 1  zx  0,25
 xy 1  yz 1  zx 1  x  y  z  x  y  2 
Dấu bằng xảy ra khi  y  z  2   1  z  x  2 
Vì x  y  z nên giả sử x  y  . z 0,25 x  y  2 x  y  2   Ta có  
1  y  z  2  x  z  4 (vô nghiệm) x z 2    x  z  2  
Vậy xy  1  yz 1  zx  1  x  y  z.
Tìm tất cả các số nguyên dương n sao cho hai số 2 n  2n  7 và 4 1,5 điểm 2
n  2n 12 đều là lập phương của hai số nguyên dương nào đó. Đặt 2 3 2 3
n  2n  7  a ; n  2n 12  b (với * a, b ) 0,25 Dễ thấy a  b Ta có 3 3 b  a   2 n  n   2 2 12 n  2n  7 19 0,25  b  a 2 2 b  ab  a  19 Vì * a, b , b  a, 2 2
b  ab  a  b  a và 19 là số nguyên tố nên HDC TOÁN CHUYÊN trang 3/5 Câu Nội dung Điểm a  2  TM  b   a 1 b 0,5   3 a  2     2 2 b   ab  a 19 a  3     L b 3  b   2 n  3 (L) 2  n  2n 15  0   n  5  n  5 (TM ) 0,5
Vậy n  5 là giá trị cần tìm.
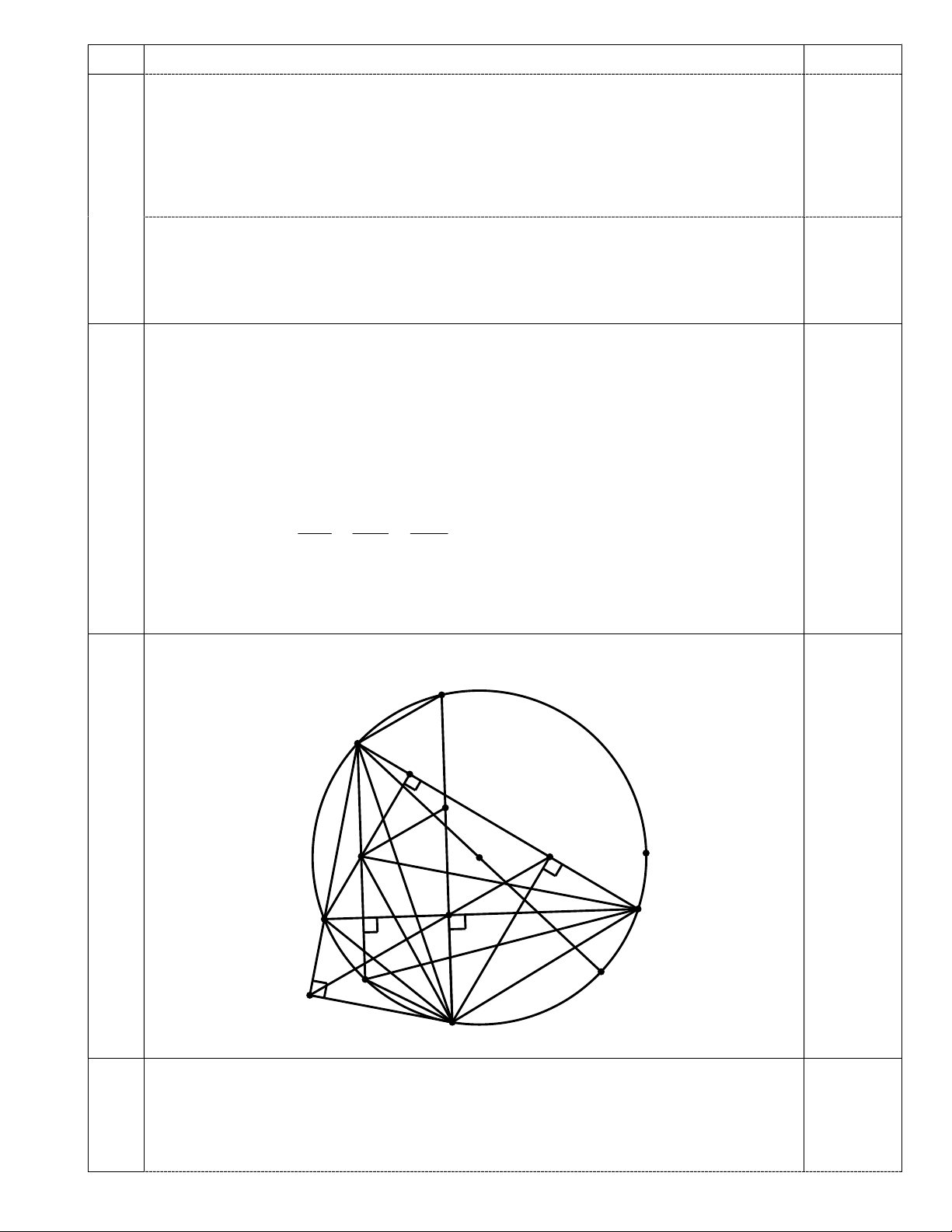
Cho tam giác nhọn ABC nội tiếp đường tròn O đường kính AE. Gọi
D là một điểm bất kì trên cung 
BE không chứa điểm A ( D khác B và
E ). Gọi H , I, K lần lượt là hình chiếu vuông góc của D lên các đường thẳng BC, CA và A . B 5
a) Chứng minh ba điểm H , I, K thẳng hàng. 3,5 điểm AC AB BC b) Chứng minh    DI DK DH
c) Gọi P là trực tâm của A
 BC, chứng minh đường thẳng HK đi qua
trung điểm của đoạn thẳng D . P Hình vẽ S A R I P O H B C Q E K D
Tứ giác BKDH nội tiếp   KBD   KHD   1 . a 0,25
Tứ giác ABDC nội tiếp   KBD  
ACD 2 (cùng bù với  ABD ) HDC TOÁN CHUYÊN trang 4/5 Câu Nội dung Điểm Từ   1 ,2   KHD   ICD 3. 0,5
Lại có tứ giác CIHD nội tiếp   IHD   0 ICD 180 4.
Từ 3, 4 suy ra  IHD   0 DHK 180 0,25  K, I, H thẳng hàng.  ∽   AK CH AB  BK CH AKD CHD g.g      KD HD KD HD 0,5 CH AB BK    5 HD KD KD  ∽  BH AI AC  IC BH AC IC BDH ADI g.g     6 b    0,5 DH DI DI DH DI DI  ∽  IC KB ICD KBD g.g    7 0,25 ID KD CH BH AB AC
Từ 5, 6 và 7 suy ra    . HD DH KD DI 0,25 AC AB BC Vậy    DI DK DH
Đường thẳng AP cắt O tại Q và đường thẳng DH cắt O tại S. Ta có  SAC   SDC (cùng chắn  CS ) 0,25
Tứ giác CDHI nội tiếp   HDC   HIA   SAC   HIA
Suy ra đường thẳng AS song song với đường thẳng HK.
Ta có AQ // DS (cùng vuông góc với BC )
 AQDS là hình thang, nội tiếp đường tròn O c
 AQDS là hình thang cân   QDS   AS . D 0,25 Qua P vẽ PR // AS   ASD   PRD (đồng vị) Suy ra  PRD  
QDR  PQDR là hình thang cân
Ta thấy BC  PQ tại trung điểm PQ , suy ra BC là trục đối xứng của 0,25
hình thang cân  HD  H . R
Xét DPR có HD  HR và HK // PR  0,25
HK đi qua trung điểm của D . P
-------------------- HẾT-------------------- HDC TOÁN CHUYÊN trang 5/5