Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2022 – 2023 sở GD&ĐT Quảng Bình

SỞ GD&ĐT QUẢNG BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2022 - 2023 ĐỀ CHÍNH THỨC Khóa ngày 07/6/2022 Môn: TOÁN (CHUYÊN)
SBD:………….. Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Đề có 01 trang gồm 5 câu
Câu 1 (2,0 điểm). Cho biểu thức 3x + 5 x −11 x − 2 2 P = ( − +
− (với 0 ≤ x ≠1) x − )1( x + 2) 1 x −1 x + 2
a) Rút gọn biểu thức P .
b) Tìm x để P chia hết cho 3.
Câu 2 (2,0 điểm). a) Cho phương trình 2 x − 2(m − ) 1 x − 3 = 0 ( )
1 (với m là tham số). Tìm tất cả các
giá trị nguyên của m để phương trình (1) có hai nghiệm x , x thỏa mãn x + 2x = 5. 1 2 1 2
b) Giải phương trình x +1 + 3x − 5 = 4.
Câu 3 (1,0 điểm). Cho a, ,
b c là độ dài ba cạnh của một tam giác. Chứng minh rằng: 2 2 2 a b c + +
≥ a + b + c
b + c − a c + a − b a + b − c
Câu 4 (1,5 điểm). Tìm n∈ để 5 n +1 chia hết cho 3 n +1.
Câu 5 (3,5 điểm).
Từ điểm A ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến AM , AN với (O) (M , N
là các tiếp điểm). Gọi E là trung điểm của AN, C là giao điểm của ME với (O) (C khác
M ) và H là giao điểm của MN và AO .
a) Chứng minh tứ giác HCEN nội tiếp.
b) Gọi D là giao điểm của AC với (O) ( D khác C ). Chứng minh tam giác MND là tam giác cân.
c) Gọi I là giao điểm của NO với (O) ( I khác N ); K là giao điểm của MD và AI . Tính tỉ số KM . KD
...........................HẾT.........................
SỞ GD&ĐT QUẢNG BÌNH HƯỚNG DẪN CHẤM
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2022 - 2023 Khóa ngày 07/6/2022 Môn: TOÁN (CHUYÊN)
(Hướng dẫn chấm gồm có 05 trang) Yêu cầu chung
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu
phải lập luận logic chặt chẽ, đầy đủ, chi tiết rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với những
bước sau có liên quan.
* Điểm thành phần của mỗi câu được phân chia đến 0,25 điểm. Đối với điểm là 0,5
điểm thì tùy tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Đối với Câu 5, học sinh không vẽ hình thì cho điểm 0. Trường hợp học sinh có vẽ
hình, nếu vẽ sai ở ý nào thì điểm 0 ở ý đó.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tùy theo mức điểm từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm Cho biểu thức 3x + 5 x −11 x − 2 2 P = ( − + − x − )1( x + 2) 1 x −1 x + 2 1 2,0
(với 0 ≤ x ≠1) điểm
a) Rút gọn biểu thức P
b) Tìm x để P chia hết cho 3.
Với 0 ≤ x ≠1 ta có: (3x+5 x − )
11 − ( x − 2)( x + 2) + 2( x − )1 −( x − )1( x + 2) P =
( x − )1( x +2) ( 0,5 3x + 5 x − )
11 − (x − 4) + 2( x − )1 −(x + x − 2) = a
( x − )1( x +2) x x ( x − )1( x + + − 7 6 7 ) x +7 = ( = = x − )
1 ( x + 2) ( x − )1( x + 2) x + 2 0,5 Vậy x + 7 P = với 0 ≤ x ≠1 x + 2 HDC TOÁN (CHUYÊN) Trang 1/5 Câu Nội dung Điểm Ta có: x + 7 5 5 7 P = =1+
⇒1< P ≤1+ = với 0 ≤ x ≠1 0,25 x + 2 x + 2 2 2 Biểu thức + P chia hết cho 3 x 7 ⇔ P = 3 ⇔ = 3 0,25 b x + 2 1 1
⇔ x + 7 = 3 x + 6 ⇔ x = ⇔ x = 0,25 2 4 Vậy 1 x = 0,25 4
a) Cho phương trình 2 x − 2(m − ) 1 x − 3 = 0 ( )
1 (với m là tham số).
Tìm tất cả các giá trị nguyên của m để phương trình (1) có hai 2 2,0
nghiệm x , x thỏa mãn x + 2x = 5. 1 2 1 2 điểm
b) Giải phương trình x +1 + 3x − 5 = 4 Ta thấy ac = 3 − < 0, m
∀ nên phương trình (1) luôn có 2 nghiệm x , x 1 2
với mọi giá trị của m .  0,25
x + x = 2m − 2 2 1 2 ( )
Theo hệ thức Vi-ét ta có:  x x = 3 − 3 1 2 ( )
a Kết hợp x + 2x = 5 với (2) ta được x = 4m − 9, 7 x = − 2m 1 2 0,25 1 2 Thay vào (3) ta có 0,25
( m − )( − m) 2 4 9 7 2 = 3 − ⇔ 8
− m + 46m − 60 = 0 ⇔ m = 2 hoặc 15 m = 4 Vậy m = 2 0,25 5 Điều kiện: x ≥ 3
x +1 + 3x − 5 = 4 ⇔ ( x +1 − 2) + ( 3x − 5 − 2) = 0 0,5 x − 3 3(x − 3) ⇔ + = 0 x +1 + 2 3x − 5 + 2 b (x ) 1 3 3  ⇔ − + = 0
 x 1 2 3x 5 2 + + − +  1 3 5 ⇔ x − 3 = 0 do + > 0, x ∀ ≥ 0,5 x +1 + 2 3x − 5 + 2 3 ⇔ x = 3 Vậy x = 3 HDC TOÁN (CHUYÊN) Trang 2/5 Câu Nội dung Điểm Cho a, ,
b c là độ dài ba cạnh của một tam giác. Chứng minh rằng: 3 2 2 2 1,0 a b c + +
≥ a + b + c điểm
b + c − a c + a − b a + b − c  x + z a =  2
x = a + b − c > 0 
Đặt  = + − > 0  x + y y b c a ⇒ b  = 2 z c a b 0  = + − >   y + z 0,25 c =  2
(x + y)2 ( y + z)2 (z + x)2 Ta cần chứng minh: + +
≥ x + y + z 4z 4x 4y
(x + y)2 ( y + z)2 (z + x)2 Ta có: xy yz zx + + ≥ + + ( ) 1 4z 4x 4y z x y Mặt khác: xy yz + ≥ 2 ; yz zx + ≥ 2 ; xy zx y z + ≥ 2x. 0,25 z x x y z y Khi đó xy yz zx + +
≥ x + y + z (2) z x y
(x + y)2 ( y + z)2 (z + x)2 Từ ( ) 1 ( , 2) ta có + +
≥ x + y + z 0,25 4z 4x 4y 2 2 2 Vậy a b c + +
≥ a + b + c
b + c − a c + a − b a + b − c 0,25
Dấu bằng xãy ra khi a = b = c
Tìm n∈ để 5
n +1 chia hết cho 3 n +1 1,5 điểm Với n∈, ta có 5 3 2
n + n + ⇔ n ( 3 n + ) − ( 2 n − ) 3 1 1 1 1 n +1 0,25 ⇔ ( 2 n − ) 3
n + ⇔ (n − )(n + )(n + )( 2 1 1 1 1 1 n − n + ) 1 0,5 2
⇔ n −1n − n +1 (vì n +1≠ 0) ⇒ n(n − ) 2
1 n − n +1⇔ ( 2 n − n + ) 2 4
1 −1n − n +1 0,25 2 n − n +1=1 n =1 2
⇔ 1n − n +1⇒  ⇔ 0,25 2
n − n +1 = 1  − n = 0
Thử lại ta thấy n = 0;
n =1 thỏa mãn để 5 n +1 chia hết cho 3 n +1 0,25 Vậy n = 0; n =1. HDC TOÁN (CHUYÊN) Trang 3/5 Câu Nội dung Điểm
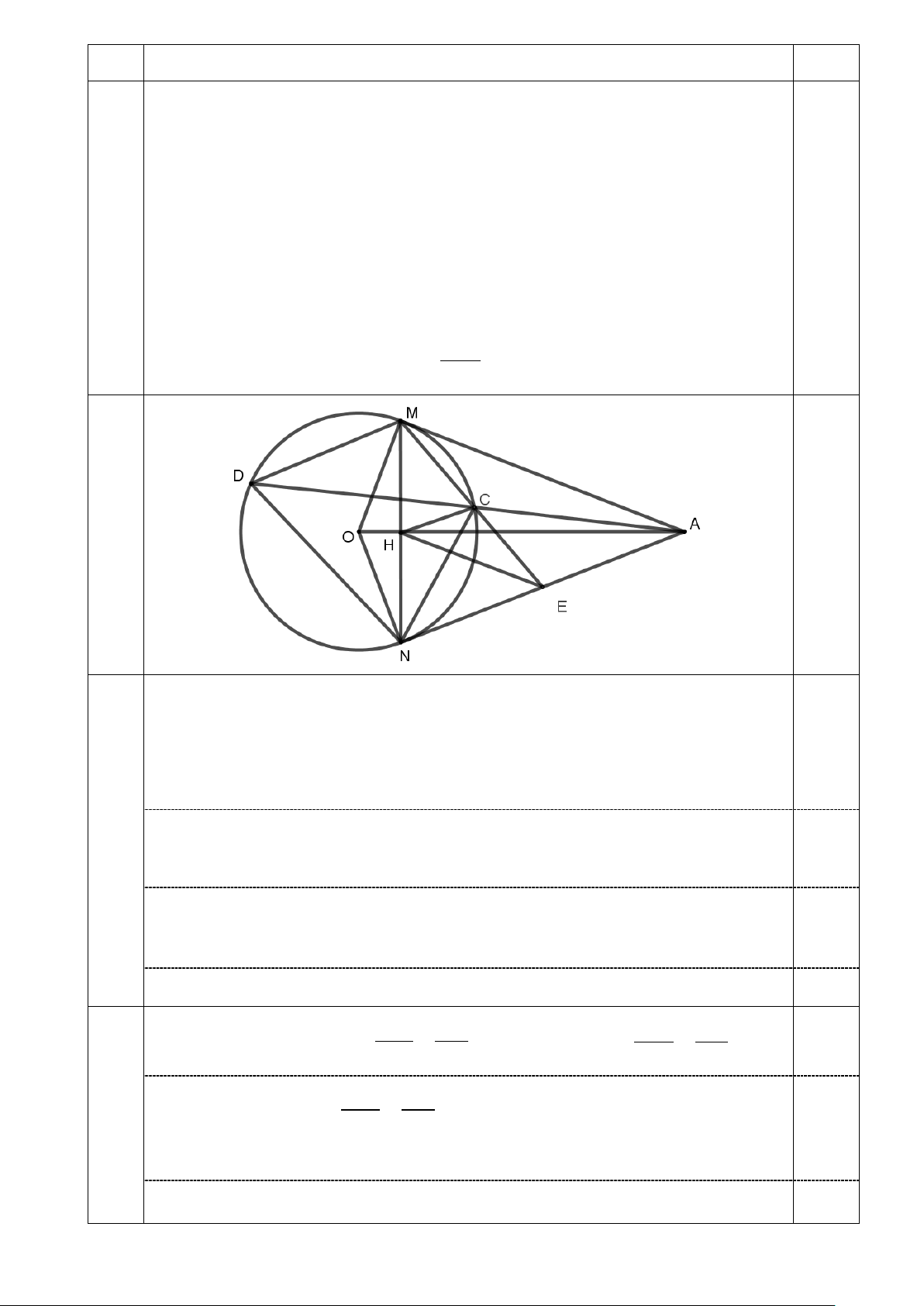
Từ điểm A ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến AM , AN với
(O) (M, N là các tiếp điểm). Gọi E là trung điểm của AN , C là giao
điểm của ME với (O) (C khác M ) và H là giao điểm của MN và AO
a) Chứng minh tứ giác HCEN nội tiếp. 5 3,5
b) Gọi D là giao điểm của AC với (O) ( D khác C ). Chứng minh điểm
tam giác MND là tam giác cân.
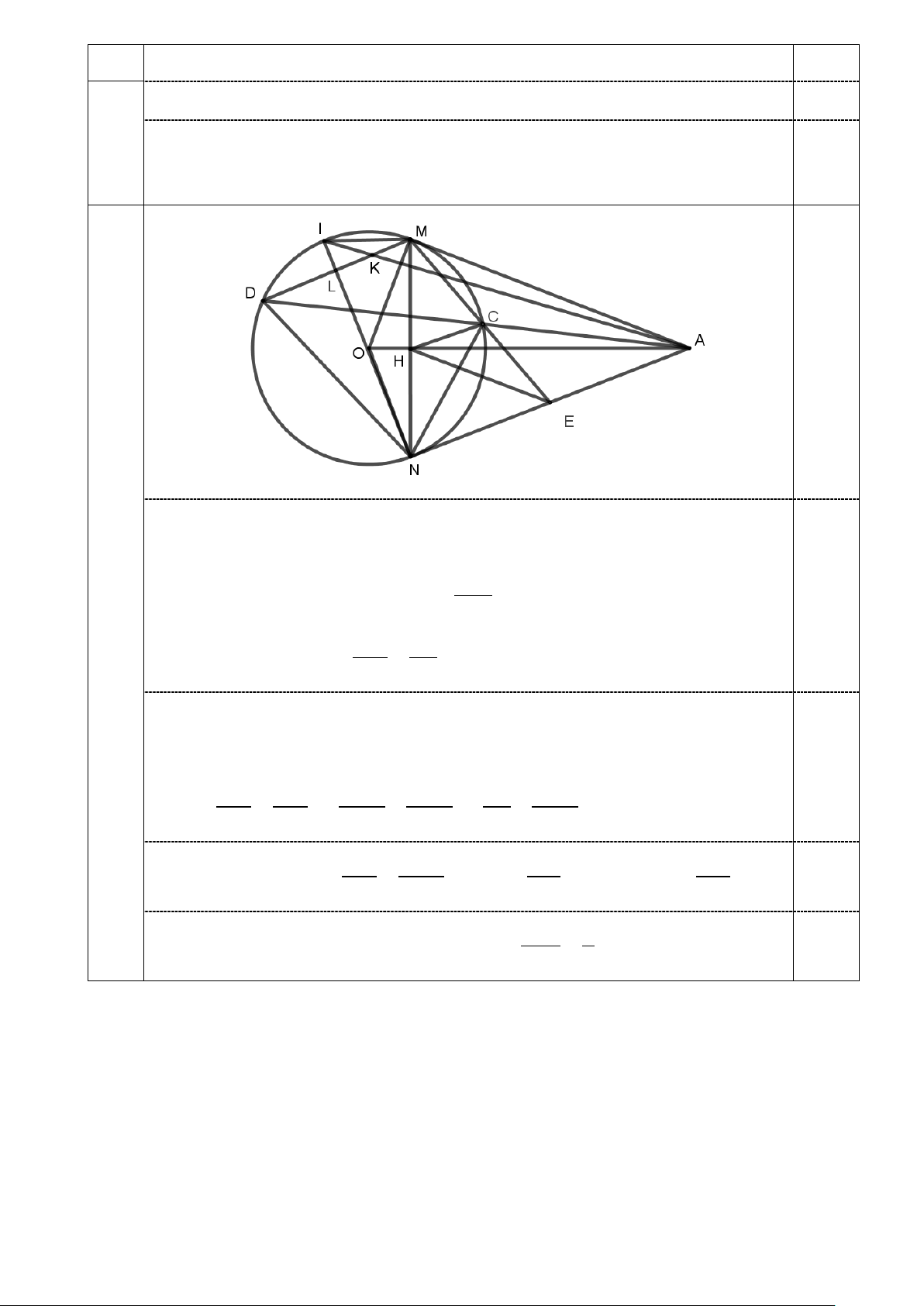
c) Gọi I là giao điểm của NO với (O) ( I khác N ) ; K là giao
điểm của MD và AI . Tính tỉ số KM . KD
Ta có AM , AN là hai tiếp tuyến cắt nhau nên OA là đường phân giác của  MON 0,25 MO ∆
N cân tại O , có OA đường phân giác nên OA đồng thời cũng là
đường trung trực ứng với MN ⇒ MH = HN; OA ⊥ MN
a Vì MH = HN; AE = EN nên HE là đường trung bình của MA ∆ N 0,5 ⇒ ⇒  =  HE / /MA HEM AME mà  = 
MNC AME (cùng chắn  MC ) 0,5 nên  =  MNC HEM
Suy ra tứ giác HCEN nội tiếp. 0,25 ∆ ∽ ∆ ( . ) EN EC ENC EMN g g ⇒ =
mà EN = EA nên EA EC = 0,25 EM EN EM EA b E ∆ CA và E ∆ AM có EA EC = và  AEC chung EM EA 0,25 Do đó E ∆ CA∽ E ∆ AM ⇒  =  EAC EMA Lại có  = 
EMA MDC (cùng chắn  MC ) nên  =  EAC MDC 0,25 HDC TOÁN (CHUYÊN) Trang 4/5 Câu Nội dung Điểm
Suy ra MD / / AN ⇒  =  DMN MNA Mặt khác,  = 
MDN MNA (cùng chắn  MN ) 0,25 ⇒  = 
MDN DMN . Do đó MN ∆ D cân tại N
Gọi L là giao điểm của MD và NI
Vì MD / / AN (cmt), IN ⊥ AN (tính chất tiếp tuyến) MD
nên IN ⊥ MD tại L ⇒ DL = ML = 2 0,25 IN LK IL ∆ A có LK / / ⇒ = c AN ( ) 1 AN IN
Ta có IM / / AO (cùng vuông góc với MN ), suy ra  =  MIL AON Lại có  =  0
MLI ONA = 90 nên MIL ∆ ∽ A
∆ ON (g − g) 0,25 Suy ra IL ML IL ML IL ML = ⇒ = ⇒ = ( 2) NO AN 2NO 2AN IN 2AN Từ ( ) 1 và (2) suy ra LK ML ML ML = ⇒ LK = ⇒ MK = KL = 0,25 AN 2AN 2 2 KM 1 Vì MK = LK; 3
ML = DL ⇒ KD = KM ⇒ = . 0,25 KD 3 HDC TOÁN (CHUYÊN) Trang 5/5
Document Outline

• 45. QUẢNG BÌNH. ĐỀ
• 45. QUẢNG BÌNH. ĐA