

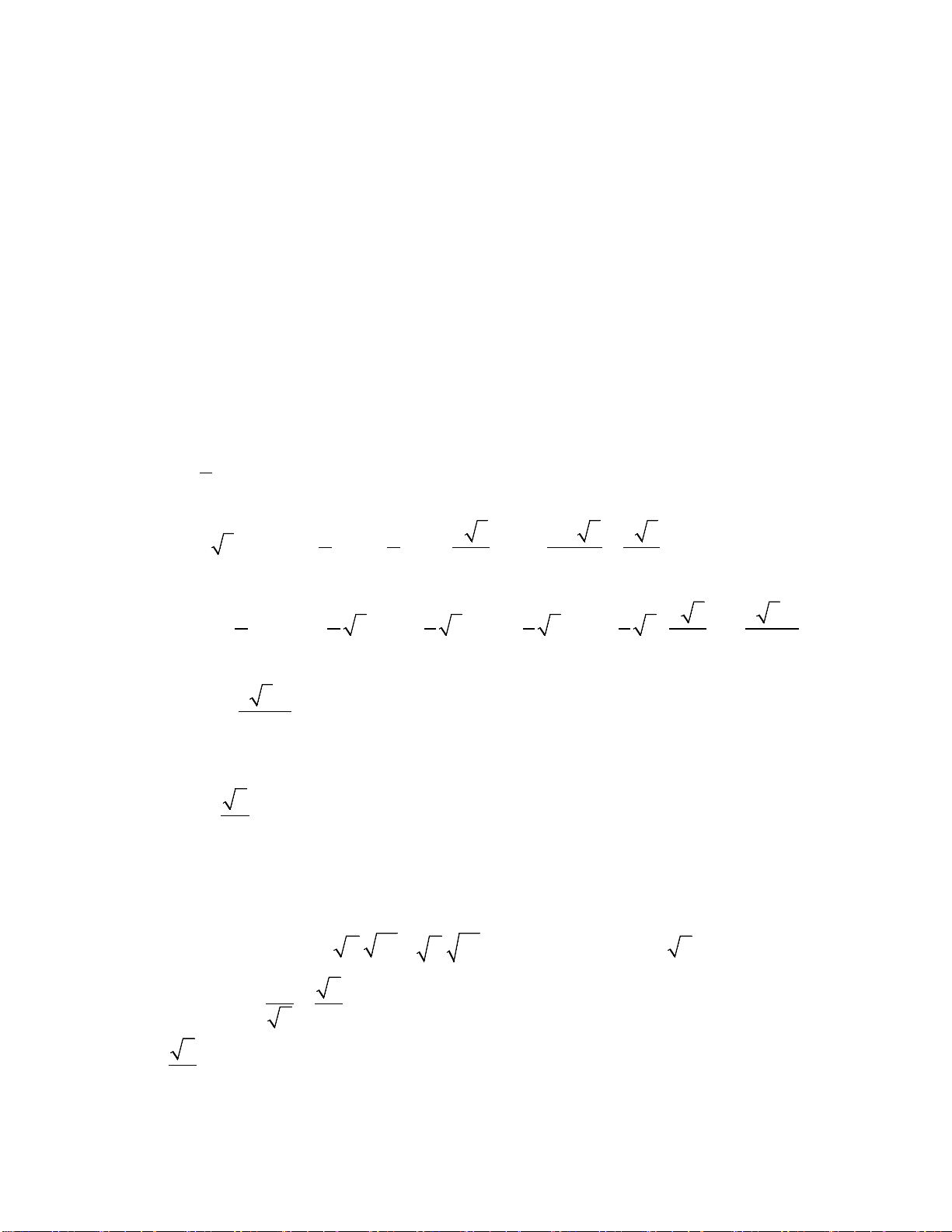
Preview text:
HƯỚNG DẪN CHẤM
Câu 1: (1,0 điểm) Rút gọn biểu thức P = 3 2 − .(2 3 − 3 2) 2 − 6 6 − 3 3( 6 −3) − 2(2 − 6) 18 − 3 3 − 2 2 + 12 P = ( − = − 2 − 6)( 6 −3) .(2 3 3 2) .(2 3 3 2) 2 6 − 6 − 6 + 3 6 3 2 − 3 3 − 2 2 + 2 3 = ( − ) 2 − 3 = ( − ) 2 6 −6−6+3 6 . 2 3 3 2 . 2 3 3 2 = 2 6 − 6 − 6 + 3 6 5 6 −12 5 6 −12 5 6 −12 = = 1 5 6 −12
Câu 2: (1,0 điểm) Cho hai đường thẳng (d1): y=(k-3)x+4 và (d2): y=(9-2k)x-5.
Tìm k để (d1) song với (d2) ( k − 3 = 9 − 2k d / / d ⇔ ⇔ k = 4 1 ) ( 2) 4≠ 5−
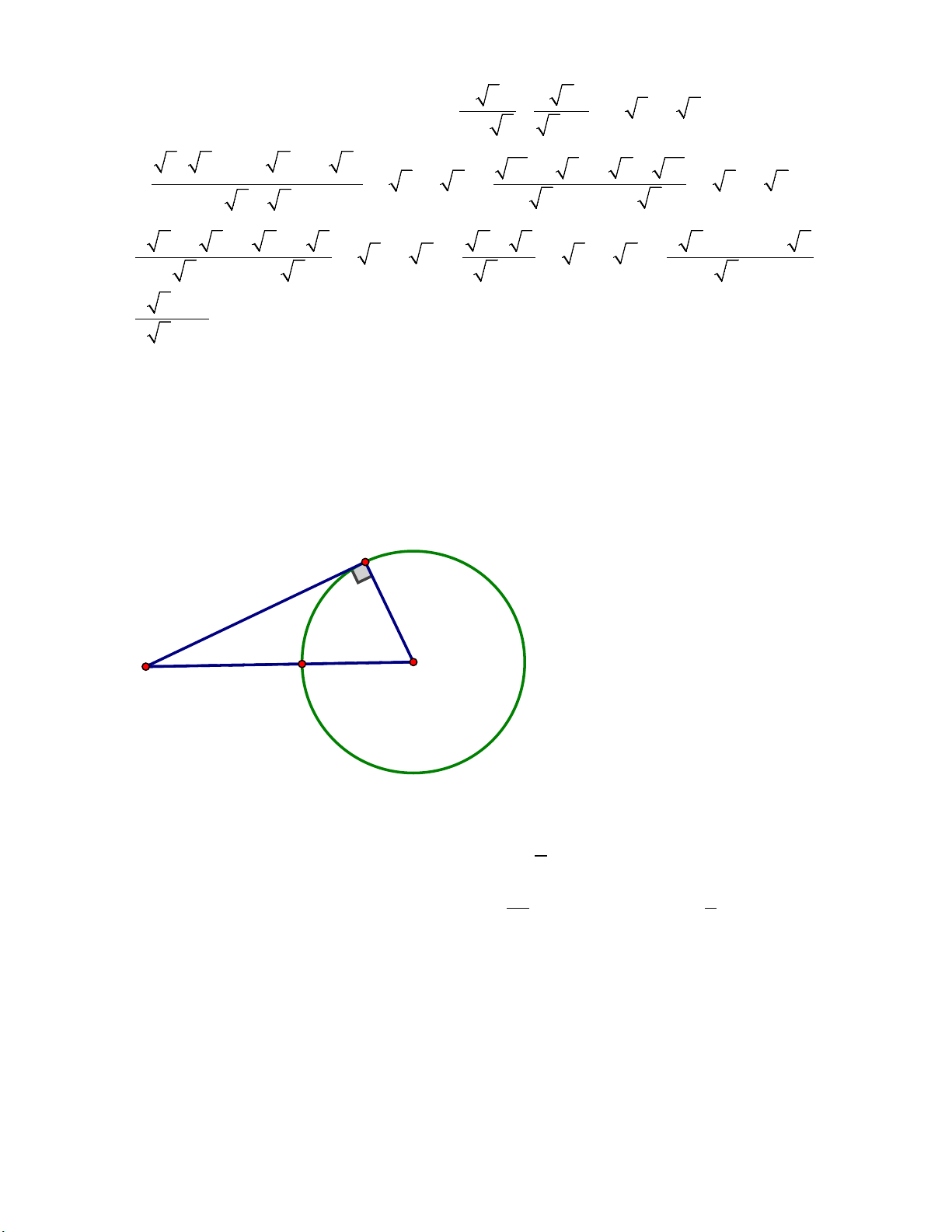
Vậy k=4 thì hai đường thẳng đã cho song song với nhau. Câu 3 B 2a a A M O
Ta có BO=OM=R (bán kính đường tròn (O) nêm AO=a+R.
Áp dụng định lý Pytago ta có: 2 2 2 = + ⇔ ( + )2 = ( )2 2 3 AO AB OB a R 2a + R ⇔ R = a 2
Câu 4: (1,0 điểm) cho đường thẳng ( ) 28 d : y = x + và parabol (P) 1 2 : y = x . Tìm tọa độ 3 3
giao điểm của (d) và (P)
Hoành độ giao điểm của hai đồ thị là nghiệm phương trình: 1 2 28 2 x − x − = 0 ⇔ x − 3x − 28 = 0 3 3 49 y = = 1 x 7 1 3 ⇔ ⇒ x = 4 − 16 2 y = 2 3
Vậy tọa độ giao điểm của hai đồ thị là 49 16 7; va 4; − 3 3
Câu 5: (1,0 điểm) Chứng minh phương trình 2 2
5x + 2y − 2xy − 4x + 4y + 5 = 0 vô nghiệm 2 2
5x + 2y − 2xy − 4x + 4y + 5 = 0 ⇔ (x − y)2 + (2x − )2 1 + (y + 2)2 = 0
Vế trái >0, đẳng thức không xảy ra nên pt vô nghiệm
Câu 6: (1,0 điểm) Tìm m, n nguyên dương để phương trình 2
x − 2(m − n)x + 2m − 3n = 0 Ta có 2 2
∆ ' = m + n − 2mn − 2m + 3n ≥ 0 x + x = 2m − 2n 1 2 x x = 2m − 3n 1 2 Theo đề bài 2 2 x + x =10 ⇔ x + x − 2x x =10 1 2 ( 1 2)2 1 2
⇔ (2m − 2n)2 − 2(2m − 3n) =10 2 ⇔ 2m − 2m(2n + ) 2 1 + 2n + 3n − 5 = 0 (*)
Phương trình (*) phải cí nghiệm nguyên: Khi 11 ∆' ≥ 0 n ≤ ⇔ 2 m,n + ∈ m,n + ∈
Suy ra n =1,2,3,4,5 với n=1,5 thì ∆' chính phương và m=3, 6
Vậy các cặp số thỏa mãn là (m,n)=(3;1); (6; 5)
Câu 7: (1,0 điểm) Cho đường tròn (O) có đường kính BC, A là điểm nằm trên (O)
(ABthứ hai là K. Đường thẳng BK cắt (O) tại điểm thứ hai là L. Cát đường thẳng CL, OK cắt
nhau tại I. Chứng minh ba điểm A, B, I thẳng hàng GIẢI
Gọi G là tâm đường tròn ngoại tiếp tam giác ABO
Góc ABC=900 ( góc nội tiếp chắn nửa đường tròn tâm O)
Suy ra B, G, K, L thẳng hàng và góc BOK =900 (góc nội
tiếp chắn nủa đường tròn tâm G) A L K G B O C
Do đó IO và BL là hai đường cao của tam giác IBC cắt nhau tại K
Suy ra KC là đường cao thứ ba hay BI ⊥KC mà BA ⊥KC suy ra B, A, I thẳng hàng
Câu 8: (2,0 điểm) Cho tam giác điều ABC cạnh a, đường cao AH (H thuộc BC), M là
điểm bất kỳ trên cạnh BC, vẽ ME vuông góc AB tại E và MF vuông góc AC tại F. Gọi O là trung điểm của AM.
a) (1,0 điểm) Tứ giác OEHF là hình gì?
b) (1,0 điểm) Tìm giá trị nhỏ nhất của diện tích tứ giác OEHF theo a khi M di động trên cạnh BC. Giải a) Ta có = = 0
AEM AHM AFM = 90 suy ra 5 điểm A, E, H, F,M cùng thuộc một đường tròn đường kính AM Do = 0 EAM FAH = 30 suy ra = 0
EOH FOH = 60 . Vậy OEHF là hình thoi b) 1 S = EF.OH OEHF 2 Mà FE=OH AB a 3 và 1 1 a 3 3 3 OH = AM ≥ AH = ; AH= = ; 2 2 4 2 2 2 2 Suy ra 1 1 2 1 2 1 2 1 a 3 3 3a S = EF.OH = 3OH = 3AM ≥ 3AH = 3 = OEHF 2 2 8 8 8 2 32 2 GTNN 3 3a S =
khi M trùng với H hay M là trung điểm của BC OEHF 32
Câu 9: (1,0 điểm) Cho các số thực x, y thỏa mãn điều kiện x ≥ 0, y ≥ 0 và 2 2 x + y =1 Chứng minh 2 3 3 ≤ x + y ≤1. 2
Giải Theo điều kiện x ≥ 0, y ≥ 0 và 2 2
x + y =1 ; 0 ≤ x ≤1,0 ≤ y ≤1 3 3 2 2 Suy ra x + y ≤ x + y =1 Maët khaùc1= ( + ) ≤ ( + )2 2 2 2 3 3 ≤ ( + )( 3 3 + ) = ( 3 3 x y x. x y. y x y x y 2 x + y ) ( 3 3 + ) 1 2 suy ra x y ≥ = 2 2 2 3 3 Vaäy ≤ x + y ≤1 2
Document Outline
- Doc1
- ĐỀ CHUYÊN TOÁN TỈNH TÂY NINH NĂM 2022




