Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2022 – 2023 sở GD&ĐT TP Đà Nẵng

HƯỚNG DẪN GIẢI
Câu 1: (1,5 điểm)   Cho biểu thức
 x 3 x 1 x 1 1  x 3       : x P
với x  0 và x 1.  x x 1 x  x 1 x 1 2x
Rút gọn biểu thức P và tìm tất cả các số tự nhiên x để giá trị biểu thức 2 x 3P là số nguyên tố. 2P
Lời giải:
Điều kiện xác định : x  0 và x 1.   Ta có:
 x 3 x 1 x1 x x 1 x 3 x x  2 x 3 2 x P       x  
1 x x   : 1  x
 x  1x x    . 2 1 x 3 
 x  1 x  3 2 x 2 x P    . x  
1 x x  . 1
x 3 x  x 1 Thay 2 x P x  P  vào biểu thức 2 3 ta được: x  x 1 2P 2 x 3 2 x 3. 1 2  x 3P x  x 1 x  x 1 x  x 2    . 2P 2 x 2 2 2. x x 1 x  x 1
Do biểu thức 2 x 3P là số nguyên tố nên x  x 2 cũng là số nguyên tố 2P 2
Ta đặt: x  x 2  p ( p là số nguyên tố)   x  1 x   2  2 p . 2
Để ý: x  2  x 1.  x 1   1  x 1  2
Do đó sẽ có hai khả năng: 
 x 0, p 1 hoặc 
 x 0,(2, p)1, p 2.
 x 2  2p    x 2  p   x 11 x  4 Khả năng 1:     (nhận).
 x 2  2p p  2  
 x 1 2 x  4 Khả năng 2:     (nhận).
 x 2  p p  5   Vậy 2 x P x  P 
và khi x  4 và x  9 thì 2 3 là số nguyên tố. x  x 1 2P Câu 2: (1,5 điểm) a) Cho phương trình 2
(5m)x (n3m)x 5 m  0 , với m và n là các tham số. Tìm tất cả các cặp số nguyên ( ;
m n) sao cho phương trình đã cho có nghiệm kép.
b) Trong mặt phải tọa độ Oxy , cho parabol 2 2
(P) : y  x , với O là gốc tọa độ. Tìm tọa độ hai điểm , A B 3
trên P sao cho tam giác OAB vuông tại O và khoảng cách từ O đến AB lớn nhất.
Lời giải:
Điều kiện xác định: m  5 Ta có: 2 2
  (n3m) 4(25mm ) .
Để phương trình có nghiệm kép thì:   0 2 2
 (n3m )4(25m )  0 2 2
 (n3m )  4(25m ) (*) 2
 25m là số chính phương. Đặt 2 2
25m  a (a  )
m  5 và n 15 Xét a  0 thì  .
m  5 và n  15  Xét a 1 thì 2
m  24 mà 24 không phải là số chính phương nên vô lí. Xét 2 a  4 thì 2
m  21 mà 21 không là số chính phương nên vô lí.
m  4 và n 12 Xét 2 a  9 thì 2 m 16 nên  .
m  4 và n  12
m3 và n9 Xét 2 a 16 thì 2 m  9 nên  .
m  3 và n  9  Xét 2 a  25 thì 2
m  0 nên m  0 và n  0 .
Vậy để các cặp số nguyên ,
m n thỏa đề là: ( ;
m n)  (3;9)  (3;9)  (4;12)  (1;12)  (0;0) . Câu 3: (2 điểm)
a) Giải phương trình 2
x 10x 11 4 2x 1  0. 4 3 2 2
2x 14x y 31 y 90xy 66  0
b) Giải hệ phương trình  . 2 2 2 2
x y2x 2y (y1)(y  y 2)  0 
Lời giải: a) 2
x 10x 11 4 2x 1  0. Điều kiện: 1 x  . 2
Phương trình (*) tương đương với: x   x  2 2 ( 4) 2 1 2 x2  0      2
x4  2x 12
x2  2x 1 (   
 x2)  2x 1    x  3 6         .
x4   2x 1  2 
6 x  2x 1 6   x 0       x  7 14   2 (6  
 x)  2x   1  
Vậy phương trình đã cho có tập nghiệm: S  3 6;7 14. 4 3 2 2
2x 14x y 31 y 90xy 66  0 (1)
b) Giải hệ phương trình  2 2 2 2
x y2x 2y (y1)(y  y 2)  0. (2) 
Xét phương trình (2) ta có: 2 2 2 2
x y 2x 2y (y 1)(y  y  2)  0 2 2 2 3
 x y 2x 2y  y 1 y 1 0 2 2
 x (y 2)  y (y 2)  y 2  0 2 2
 (x  y 1)(y 2)  0 Vì 2 2
x  y 1 0  y  2 Thay vào (1) ta được: 4 3 2 2
2x 14x y 31x y 90xy 66  0 4 3 2
 2x 28x 124x 180x  66  0 4 3 2
 x 14x  62x 90x 33  0 4 3 2
 x 14x  62x 90x 33 4 3 2 3 2 2
 x 8x 11x 6x  48x 66x 3x 24x 33  0 2 2 2 2
 x (x 8x 11)6x(x 8x 11) 3(x 8x 11)  0 2 2
 (x 8x 11)(x 6x 3)  0 2
x 8x 11 0    . 2
x 6x 3  0 
Tự giải phương trình bậc hai ra được các cặp số x, y thỏa đề là : ( ; x y) 4 5;  2 ,4 5;  2 ,3 6;  2 ,3 6;  2 Câu 4: (2 điểm)
a) Tìm tất cả các cặp số nguyên ( ; a b) thỏa mãn 3 2
a  (b  a)b 5 .
b) Cho phương trình 2 2
x 2x  k 3k 9  0 , với k là tham số. Khi phương trình đã cho có hai nghiệm
x x hãy tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
Q  x  x  x  k 10  x 2x 1 . 1, 2 1 2 1 2 2
Lời giải:
a) Tìm tất cả các cặp số nguyên ( ; a b) thỏa mãn 3 2
a  (b  a)b 5 . Ta có: 3 2
a  (b  a)b 5 3 3
 a b  ab 5 (*) 2 2
 (ab)(a  ab b )  ab 5 .
Trường hợp 1: a  b  ab   2 a  ab  2 b  2 a  2 5 b  5
a  2, b   1 (laáy)
a1; b  2 (loaïi)   .
a  1; b    2 (laáy)
a2; b  2 (loaïi)
Trường hợp 2: a  b adm
Gọi d  (a,b) thì ta có:  1 
(m ,m ) 1 và m  m . 1 2 2 1 b   dm  2 2 d 1 Thay vào (*) ta được: 3 3 3 3 2
d m d m  d m m 5 2 3 3
 d (m m mm m )  5   . 1 2 1 2 1 2 1 2  3 3 (
 m m m m  5  1 2 1 2
Từ đây ta sẽ có được: 3 3
m  m  m m 5 1 2 1 2 Nếu m m  0 thì 3 3
m  m (Vô lí) 1 2 1 2
Do đó m m  0 hay a  0 và b  0 1 2 Ta lại có: 3 2
a  (b  a)b 5
VT < 0 mà VP > 0 do đó trường hợp này không có cặp số nguyên ( ; a b) thỏa để Vậy cặp số nguyên ( ;
a b) thỏa để là (a;b)  (2;1)  (1;2) b) 2 2
 1(k 3k 9)  0  k 3k 10  0  (k 5)(k  2)  0  2  k  5 .
x  x  2  x  2 x Theo định lí Vi-ét: 1 2 2 2  2
x x  k 3k   9  1 2
Thay Q vào ta được: 2 2
(2 x)  x (2 x )  k 10  (x1) 2 2 2 2
 x 2x 1 k 11 (x 1)  112  3 . 2 2 2
Vậy Q  3 khi k  2 và x  x 1. min 1 2 Ta xét: 2 2
x  x  x  k 10  x 2x (x  x )  k 10 1 2 1 1 1 1 2
Vì x là nghiệm của phương trình 2 2
 x 2x  93k k 1 1 1 Thế vào trên 2 2
 93k k  2 k 10  k   4k  21 Xét 2
x 2x 1 tương tự như thế x cũng là nghiệm của phương trình 2 2 2 2 2 2
 x 2x 1103k k 2 2  Q  k   4k  21 k  3k 10 2 2
 (5k)(k  2)  (7k)(k 3)  (5k  k 3)(k  2 7k)  6 2  Q  6 2 Vậy Q  6 2 khi 29 k  . max 17 Câu 5: (1,5 điểm)
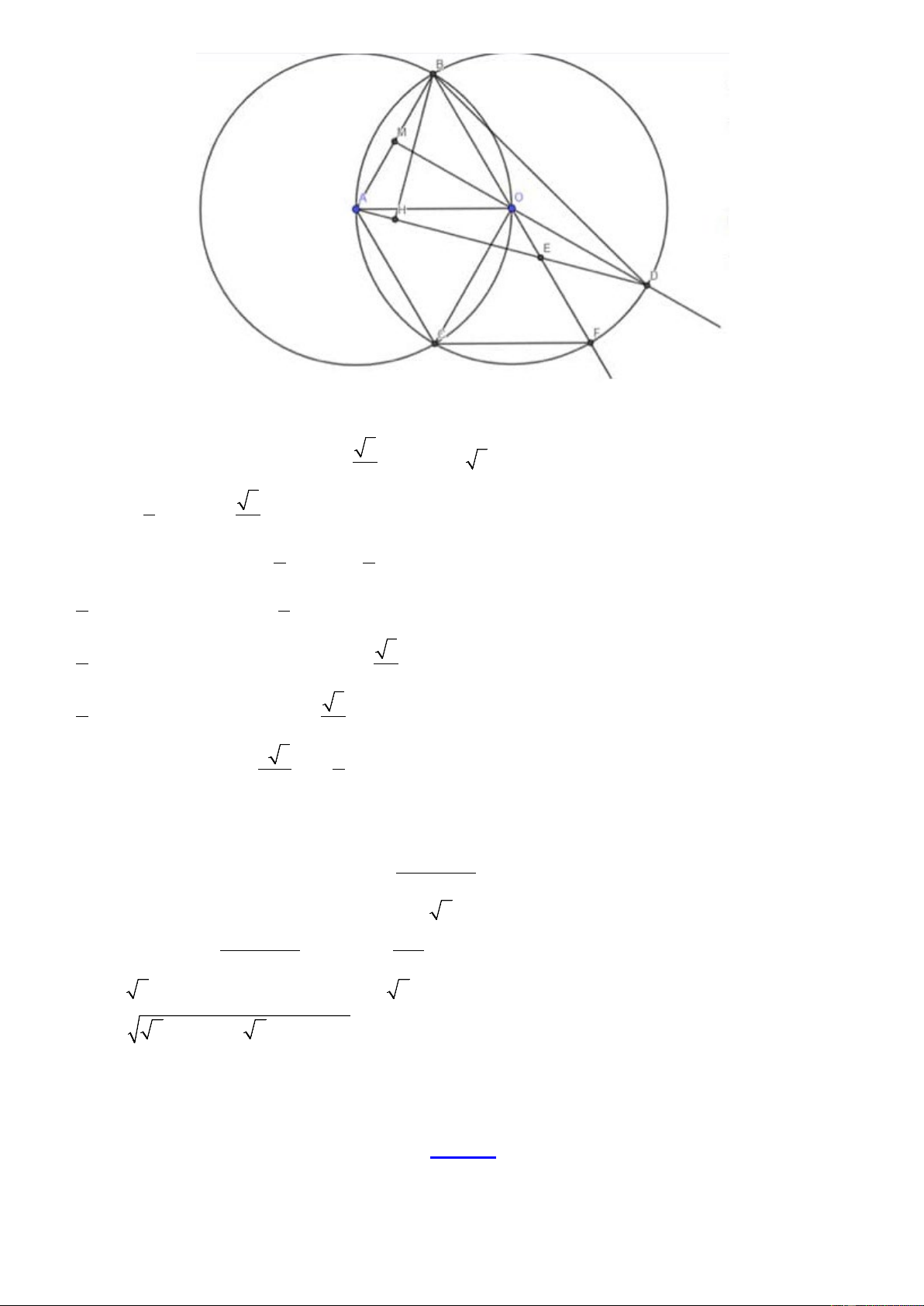
Cho đường tròn (O) bán kính R và điểm A nằm trên đường tròn. Đường tròn ( ;
A R) cắt đường tròn (O)
tại hai điểm B và C . Gọi M là trung điểm của AB , tia MO cắt (O) tại điểm D . Tia BO cắt AD tại E
và (O) tại điểm thứ hai là F . Tính độ dài đoạn thẳng DE và diện tích tứ giác ACFE theo R .
Lời giải:
Ta có: AO  AC  OC  A  OC đều mà  
AOF  2ABF  2.60 120  C
 OF đều  AOFC là hình
thoi, AF cắt OC thì I là trung điểm AF . Ta có:   3
AI  cos AOI.AO  sin 60 .R 
R  AF  3R 2 1 3 2  S  OC AF  R AOFC . 2 2 Ta có: 1 1 S  S  S
 BH AE  OM AB AOE ABE ABO . . 2 2 1  1
 .sin 75 .AB(AH  HE) sin 60 .O . B AB 2 2 1  2   3 2
 .sin 75 .R (cos 75 .AB sin 75 .AB) R 2 4 1  2   3 2
 .sin 75 .R (cos 75 sin 75 ) R 2 4 3 3 2 1  2  S  S  S  R  R    . AEFC AFOC AOE sin 75 (cos75 sin 75 ) 4 2 Ta có: 2 E  OD ∽ E
 DB  ED  E . O EB .
Ta có: OA  OB  AB  OA 
B đều nên   
BOA  60  BDA  30       180 30
 BEA 180 OBA DAB 180 60   45 2
Kẻ BH ⊥ AE  B
 HE vuông cân  BE  BH. 2   Ta có:  180 30 sin  sin  sin 75 BH BAH 
 BH  sin 75 .AB  sin 75 .R 2 AB
 BE  2 sin 75 .R  EO  BE  R  R 2 sin 75   1  2  ED 
2 sin 75 R ( 2 sin 75 1) . Câu 6: (1,5 điểm)
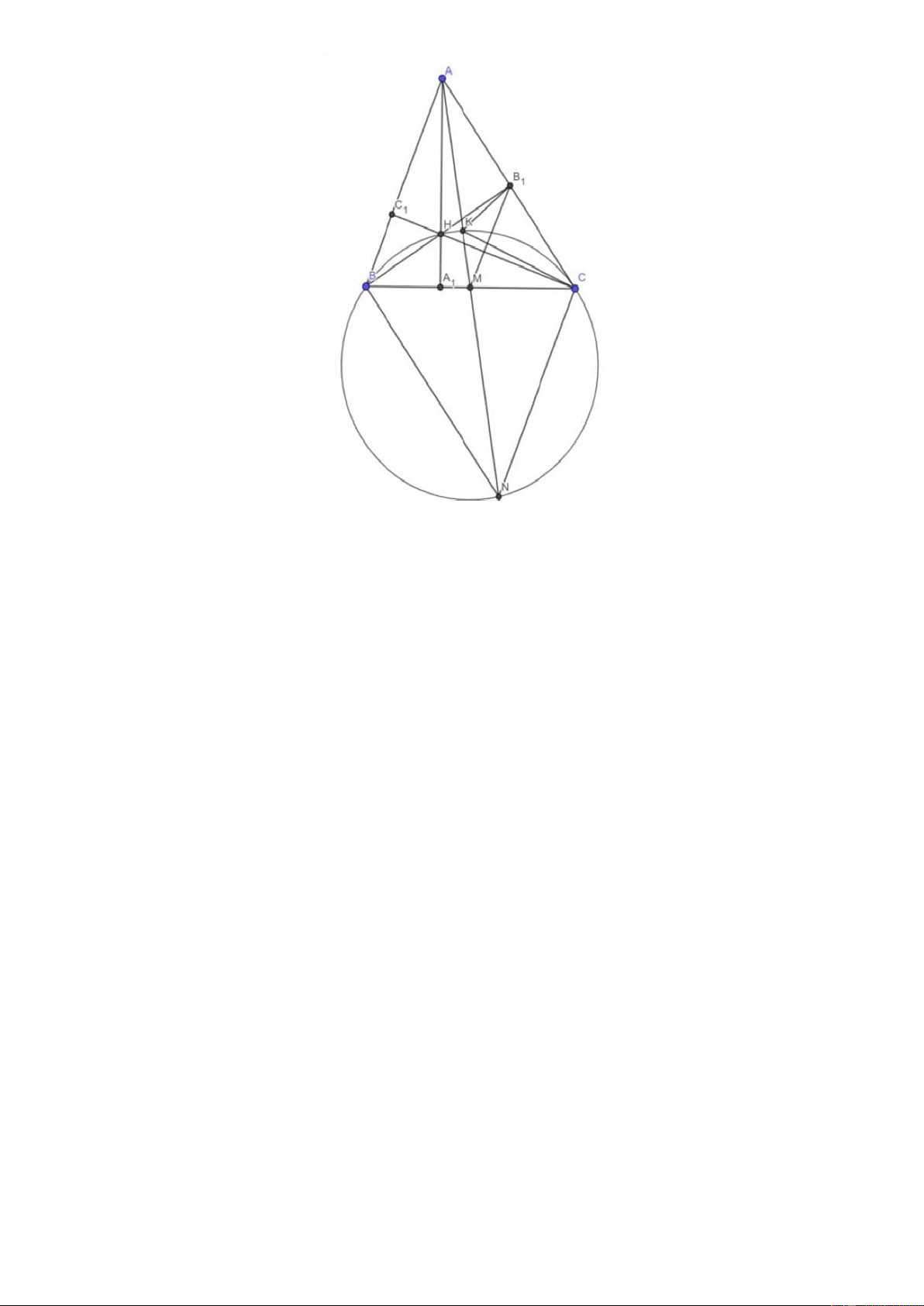
Cho tam giác ABC chọn AB  AC , trực tâm H và nội tiếp đường tròn (O) . Gọi M là trung điểm của BC
và K là hình chiếu của H trên AM . Tia AM cắt đường tròn ngoại tiếp tam giác BKC tại điểm thứ hai là
N . Chứng minh rằng tứ giác ABNC là hình bình hành.
Lời giải:
Cần chứng minh ABNC là hình bình hành  cần chứng minh MA  MN
Ta có: BKCN nội tiếp 2  MK.MN  . MB MC  MC .
Thật vậy, gọi A , B , và C lần lượt là chân đường cao từ ,
A B, C lên BC, AC, AB 1 1 1 Ta có: B
 B C vuông có M là trung điểm BC nên MB  MC  MB . 1 1 Suy ra cần chứng minh 2
MB  MK.MA. 1
Ta có: AHKB nội tiếp  
AKG  AB H  AKB  AHB . 1    1 1 1 A HB C nt        
 AKB  AHB  B CM  MB C 180  AKB 180  MB C  
 MKB  MB A 1 1 1 1 1 1 1 1 1 1  MK  B ∽ MB 
A  MK.MA , suy ra điều phải chứng minh. 1 1
--------------------------------------------
Document Outline

• de-tuyen-sinh-lop-10-mon-toan-chuyen-nam-2022-2023-so-gddt-tp-da-nang
• 15. ĐÀ NẴNG