Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2022 – 2023 trường chuyên Quốc học Huế

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT THỪA THIÊN HUẾ CHUYÊN QUỐC HỌC HUẾ NĂM HỌC 2022-2023 ĐỀ THI CHÍNH THỨC
Môn thi: TOÁN (CHUYÊN TOÁN)
Thời gian làm bài: 150 phút (không kể thời gian phát đề)  
Câu 1: (1,5 điểm) Cho biểu thức  x  2 x 2 A      
.x x  x x  0; x   1 .
 x  2 x 1 x1  a) Rút gọn biểu thức . A
b) Tìm tất cả số nguyên x sao cho biểu thức A nhận giá trị là số nguyên.
Câu 2: (1,5 điểm)
a) Trên mặt phẳng tọa độ Oxy, cho parabol P 2
: y  x và đường thẳng d: y  kx  2. Gọi I là
giao điểm của d và trục tung. Tìm tất cả các giá trị của để đường thẳng d cắt Ptại hai điểm
phân biệt A 1x; 1y, B 2
x ; y2 thỏa mãn 1x  2
x và IA  2 . IB  3 2 x  xy  
x y  
1 x  y 0
b) Giải hệ phương trình:  .  2
x2y  y 1 0 
Câu 3: (2,0 điểm)
a) Tìm m để phương trình: 2
x  m  2 3 4
1 xm 4m5  0 ( x là ẩn số) có hai nghiệm 1x, 2 x sao 3 3 cho biểu thức 1 x 2 x P  
đạt giá trị lớn nhất. 3 3 2 x 1 x
b) Giải phương trình  2 x   2
x  x   2 6 6 12
3x 10x   28 x 1  0
Câu 4: (3.0 điểm ) Cho đường tròn O và dây BC cố định không đi qua .
O Điểm A thay đổi trên cung
lớn BC sao cho tam giác ABC là tam giác nhọn AB  AC. Gọi AD, BE, CF là các đường cao và H
là trực tâm của tam giác ABC. Gọi K là giao điểm của hai đường thẳng BC và EF; I là giao điểm thứ
hai của KA với O; M là trung điểm BC; N là giao điểm thứ hai của AH và O. Chứng minh:
a) Tứ giác AIFE là tứ giác nội tiếp.
b) Ba điểm M , H, I thẳng hàng.
c) Tứ giác INMO là tứ giác nội tiếp.
d) Đường thẳng IN luôn đi qua một điểm cố định khi A thay đổi.
Câu 5: (2,0 điểm)
a) Tìm tất cả số nguyên x, y thỏa mãn 3 2
x  x y  
1  x7  y4 y  0.
b) Cho x, y, z là các số thực dương thỏa mãn xy  yz  zx  3. Chứng minh rằng x y z
3 x  y  z    . 2 2 2
. x 15 y 15 z 15 32 .
------------------HẾT----------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT THỪA THIÊN HUẾ CHUYÊN QUỐC HỌC HUẾ NĂM HỌC 2022-2023 ĐỀ THI CHÍNH THỨC
Môn thi: TOÁN (CHUYÊN TOÁN)
Thời gian làm bài: 150 phút (không kể thời gian phát đề) ĐÁP ÁN CHI TIẾT  
Câu 1: (1,5 điểm) Cho biểu thức  x  2 x 2 A        
. x x  x x 0;x   1 .
 x  2 x 1 x1  a) Rút gọn biểu thức . A
b) Tìm tất cả số nguyên x sao cho biểu thức A nhận giá trị là số nguyên. Lời giải:   a)  x  2 x 2 A         . x x  x
 x  2 x 1 x1     x 2 x 2       . x x1    x  2 1
 x  1 x     1 
 x  2 x 1 x 2. x  1     . x x 1 x 1 2      
 x  1  x  1   
x x 2 
x x 2     . x x 1 x 1 2      
 x  1  x 1       2 x     2  . 1 1 x x x x  2    
 x    x  x 1 1 1  b) Ta có 2x 2 A   2 x 2 x 1 x 1
Để A là số nguyên thì 2 x và 2 phải là số nguyên x 1 x  0
Ta có 2 là số nguyên khi  x 1 x 1(loai)  Thử lại
Với x  0  A  0 (TM)
Vậy x  0 thì A là số nguyên.
Câu 2: (1,5 điểm)
a) Trên mặt phẳng tọa độ Oxy, cho parabol P 2
: y  x và đường thẳng d: y  kx  2. Gọi I là
giao điểm của d và trục tung. Tìm tất cả các giá trị của để đường thẳng d cắt Ptại hai
điểm phân biệt A 1x; 1y, B 2
x ; y2 thỏa mãn 1x  2
x và IA  2 . IB  3 2 x  xy  
x y  
1 x  y 0
b) Giải hệ phương trình:  .  2
x2y  y 1 0  Lời giải
a) Vì I là giao điểm của d và trục tung nên I 0;2
Phương trình hoành độ giao điểm của P và d là 2 2
x  kx  2  x kx2  0   1 Ta có 2 
 k 8 0 với mọi k Và 1x. 2 x  2  0 Nên phương trình  
1 luôn có 2 nghiệm phân biệt thỏa mãn 1x  0  2 x với mọi k
x  x  k
Theo hệ thức vi-ét, ta có: 1 2 
 1x. 2x 2 x  2x
Vì IA  2IB nên ta có 1 2    1 x  2 2 x Mà 1x  0  2
x nên 1x 2 2 x  1x  2 x  k   2   2  2 x  2
x .x 2  x 1 Ta có  1 2   2    1x  0  2 x         1 x 0 2 x k     1    2 x  k         1 x 2 2 x
Vậy k  1thõa mãn yêu cầu bài toán.  3 2 x  xy  
x y  
1 x  y 0 xx yx  yx y  
1 x  y 0 b) Ta có:       2  2
x2y  y 1 0 
x2y  y 1 0 
x  y  0
x  y  0   (1)    2  x  y  
 2x xyx y 1 0  
 x2y  y 1 0 2   
  x  xy  x  y 1 0     2
x2y  y 1  2   0    
x  xy  x  y 1 0  2 
x2y  y 1 0    (2)  2 
 x2y  y 1 0    1  3 x   2    1 3    0 y x y x  y  
Giải hệ phương trình       2 1 :    2 2
x2y  y 1 0  
 2y 2y 1 0       1 3   x    2   1 3   y     2  2  2
x  xy x  y1 0   x  xy    2 2y     2 2 1 1 0
x  xy2y  0
Giải hệ phương trình 2:        2   2 2
x2y  y 1 0 
x y  2y 1
x y  2y 1    1  3 x   2    1 3 y   2 
x y  1 3     x    
 x  yx y  2    2 2 0  
 x y  2y 1           2  1 3
x y  2y 1  x  2y   y       2  2
x y  2y 1     x  2  y   1   x 1    1 y    2
Vậy hệ phương trình đã cho có 4 nghiệm:                      x y 1 3 1 3 1 3 1 3               1 ; ; ; ; ; 2;1 ;  1;    2 2     2 2     2     
Câu 3: (2,0 điểm)
a) Tìm m để phương trình: 2
x  m  2 3 4
1 xm 4m5  0 ( x là ẩn số) có hai nghiệm 1x, 2 x sao 3 3 cho biểu thức 1 x 2 x P  
đạt giá trị lớn nhất. 3 3 2 x 1 x
b) Giải phương trình  2 x   2
x  x   2 6 6 12
3x 10x   28 x 1  0 Lời giải a) Ta có: 2
ac  3m 12m15  3m  22 3 0, m nên phương trình luôn có 2 nghiệm phân biệt trái dấu  44m  1x  2 x  
Theo hệ thức vi-ét, ta có:  3  2  m  4m5  1 x . 2 x   3 3   Đặt  1 x t       t  0   2 x    Lúc đó: 1 1 P  t     t     2 t  t  1
P đạt giá trị lớn nhất là 2 khi t   t 1 1x  2 x  m 1. t b)  2 x   2
x  x   2 6 6 12
3x 10x   28 x 1  0
Điều kiện : x 1. Ta có:
 2x 6 2x 6x12 2
3x 10x   28 x 1  0
 2x 6 x 6 6x 1 3   2 x 6 10x  1           x 1  0  1     2
a  x 6, a  0 Đặt  b
  x1, b 0  Phương trình   1 trở thành: 2 a a  b  2 a  b  2
b   a a  b  2 6 3 10 0 6
3a 10b b
 a a 6b 3a 10b 2 b  a a 6b 3a 10b 2 2 2 2 2 2 2 2 2 b  0 3 2 3 2 2 4 6      3 60 100  0 a      3 a       60 a a a b ab b 100  0 2    2  2 b b  b  a  10 2 b 
Giải phương trình ta được  a   2 (l) 2 b   a   5 (l) 2 b x   Suy ra 2 2 a b x x  2 5 29 10 6 10 1 x 10x 4 0            (TM )  x  5 29 
Vậy x  5 29; x  5 29
Câu 4: (3.0 điểm ) Cho đường tròn O và dây BC cố định không đi qua .
O Điểm A thay đổi trên cung
lớn BC sao cho tam giác ABC là tam giác nhọn AB  AC. Gọi AD, BE, CF là các đường cao và H
là trực tâm của tam giác ABC. Gọi K là giao điểm của hai đường thẳng BC và EF; I là giao điểm thứ
hai của KA với O; M là trung điểm BC; N là giao điểm thứ hai của AH và O. Chứng minh:
a) Tứ giác AIFE là tứ giác nội tiếp.
b) Ba điểm M , H, I thẳng hàng.
c) Tứ giác INMO là tứ giác nội tiếp.
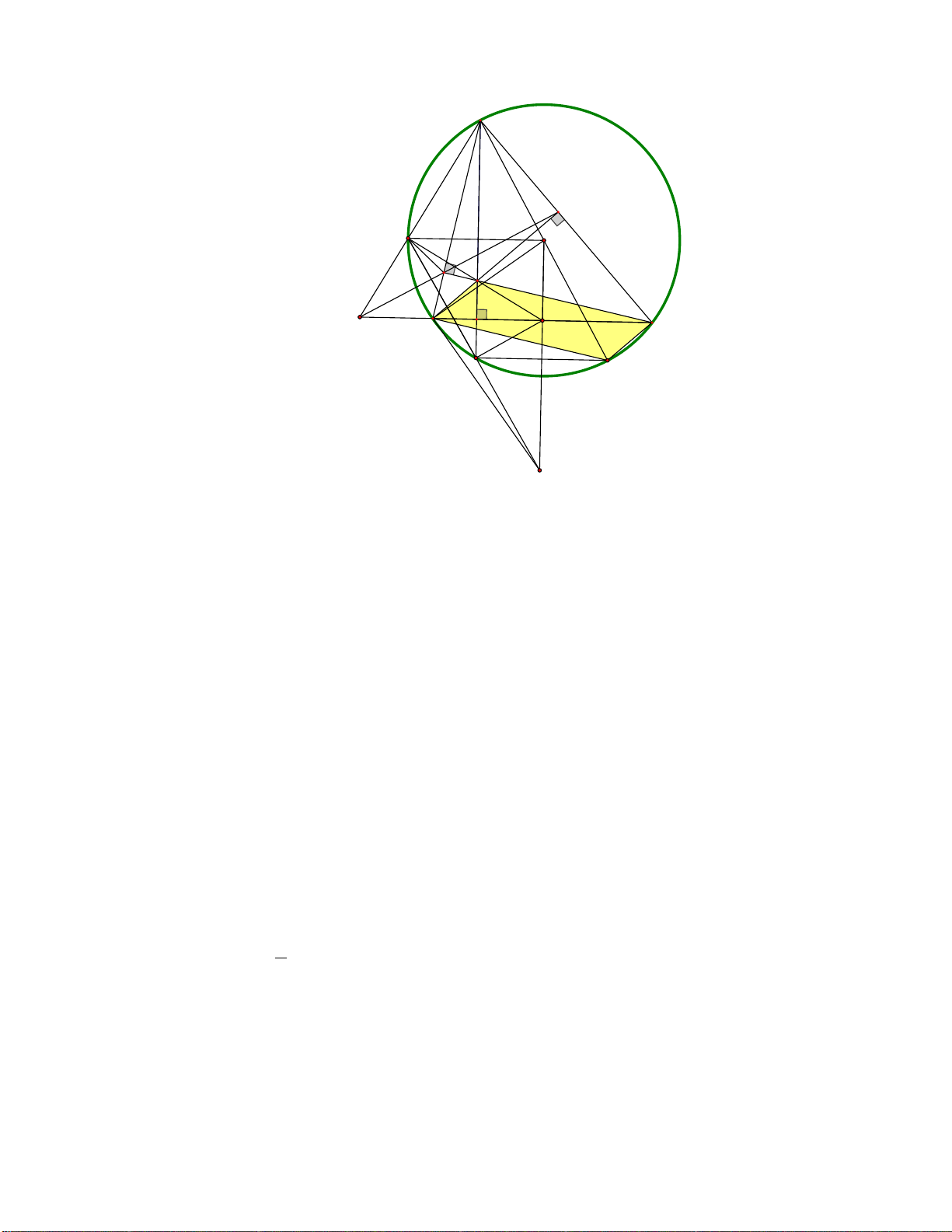
d) Đường thẳng IN luôn đi qua một điểm cố định khi A thay đổi. Lời giải A E I O F H K B D M C N T S
a) Vì tứ giác AIBC nội tiếp đường tròn nên KI.KA  . KB KC
Dễ thấy tứ giác BEFC nội tiếp nên KF.KE  . KB KC
Suy ra KI.KA  KF.KE
Vậy tứ giác AIFE nội tiếp.
b) Kẻ đường kính AT của đường tròn O. Khi đó,  90o AIT  (1)
Xét tứ giác BHCT, ta có: CC//BT (cùng  AB ); CC//BT (cùng  AC )
Nên tứ giác BHCT là hình bình hành
Suy ra M là trung điểm HT của hay M , H, T thẳng hàng.
Tứ giác AFHE là tứ giác nội tiếp đường tròn đường kính AH.
Ta có tứ giác AIFE nội tiếp nên I thuộc đường tròn đường kính AH hay  90o AIH  (2)
Từ (1) và (2) suy ra I, H, T thẳng hàng
Vậy M , I, H thẳng hàng. c) Ta có  1  NIT  NOT   3 2 Ta có   90o ANT
 NT  AN; BC  AN nên NT //BC
Mà OM  BC nên OM  NT Xét N
 OT có ON  OT và OM  NT nên OM là tia phân giác góc  NOT Suy ra  1  NOM  NOT 4 2 Từ   3 và 4 suy ra   NIM  NOM
d) Gọi S là giao điểm của tiếp tuyến đường tròn O tại B và OM. Suy ra S cố định.
Ta cần chứng minh I, N, S thẳng hàng
Gọi L là giao điểm của IS và đường tròn O Vì OB  S vuông nên 2
SB  SM.SO  . SL SI
Suy ra tứ giác OMLI nội tiếp
Ta có tứ giác OMLI và OMNI cùng nội tiếp đường tròn ngoại tiếp O
 MI và cắt O tại giao
điểm thứ hai là L và N nên N và L trùng nhau.
Vậy I, N, S thẳng hàng hay IN đi qua S cố định.
Câu 5: (2,0 điểm)
a) Tìm tất cả số nguyên x, y thỏa mãn 3 2
x  x y  
1  x7  y4 y  0.
b) Cho x, y, z là các số thực dương thỏa mãn xy  yz  zx  3. Chứng minh rằng x y z
3 x  y  z    . 2 2 2
. x 15 y 15 z 15 32 Lời giải a) Ta có: 3 2
x  x y  
1  x7  y4 y  0. 3 2
 x  x  7x4 y 2 x  x   1  0   2 x  x  
1 x y 2 2 x  x   1  2 2 x 4x   3   2 x  x  
1 x y  2 2x  1 x  3
Biện luận theo x ta có các bộ số thỏa mãn  ; x y   0;4;1;  3 ;3;  5 . b) Ta có: x x x x x     2 2 2 x 15 x 312
x  xy  yz  zx 12 x  yx  z12 4 x  yx  z8  1  1 1     x     
  (Theo bất đẳng thức 1 1 1 1       )  4    
4 x  yy  z 8
a b 4a b   x 1  1 1       1 
   (Theo bất đẳng thức 1 1 1 1      ) 16 2   x  y z 2     ab 2a b x x x    .
32x  y 32y  z 32 Tương tự y y y y    2
y 15 32y  z 32z  x 32 z z x z    2
z 15 32z  x 32x  y 32 Suy ra x y z   2 2 2
x 15 y 15 z 15 x x x y y y z x z          .
32x  y 32y  z 32 32y  z 32z  x 32 32z  x 32x  y 32
3 x  y  z  . 32 Vậy: x y z
3 x  y  z    . 2 2 2
x 15 y 15 z 15 32
Dấu " "xảy ra khi x  y  z 1.
Document Outline

• de-tuyen-sinh-lop-10-mon-toan-chuyen-nam-2022-2023-truong-chuyen-quoc-hoc-hue
• 56. CHUYÊN QUỐC HỌC QUÊ