Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2022 – 2023 trường chuyên Sơn La

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT SƠN LA NĂM HỌC 2022 - 2023
MÔN THI: TOÁN (Chuyên) ĐỀ CHÍNH THỨC Ngày thi: 07/06/2022
Thời gian làm bài: 150 phút ĐỀ BÀI:
Câu 1. (2,0 điểm)  2 x + 5   3
Cho biểu thức: A   : 1  = + −
(x ≥ 0 ; x ≠ 1 ; x ≠   4)  x +1
x − x − 2   4 − x  a) Rút gọn biểu thức . A
b) Tìm các giá trị nguyên của x để A đạt giá trị nguyên.
Câu 2. (2,0 điểm)
y − 2x −1 = 0
a) Giải hệ phương trình:  2 2
4x − 3xy + y =1 b) Giải phương trình: 2 x + x + = ( 2 2 7 3 x + ) 1 (x + 3)
Câu 3. (2,0 điểm)
a) Tìm giá trị của tham số k để đường thẳng (d : y = −x + 2 1 ) cắt đường thẳng
(d : y = 2x +3− k tại một điểm nằm trên trục hoành. 2 )
b) Trong mặt phẳng tọa độ Oxy , cho parabol (P) 2
: y = x và đường thẳng
(d): y = 2mx − m +1 (Với m là tham số). Tìm tất cả các giá trị của m để (d ) cắt (P) tại hai điểm
phân biệt có hoành độ x ; x thỏa mãn: x − x > 3. 1 2 1 2
Câu 4. (2,5 điểm)
Cho ∆ ABC có ba góc nhọn ( AB > AC) nội tiếp đường tròn (O ; R). Đường cao AH của
∆ ABC cắt đường tròn (O ; R) tại điểm thứ hai là D . Kẻ DM ⊥ AB tại M.
a) Chứng minh tứ giác BMHD nội tiếp được đường tròn và DA là tia phân giác của  MDC .
b) Từ D kẻ DN ⊥ AC tại N. Chứng minh ba điểm M , H, N thẳng hàng. c) Cho 2 2 2 2
P = AB + AC + BD + CD . Tính giá trị biểu thức P theo R .
Câu 5. (1,0 điểm)
a) Cho x, y là các số thực dương thỏa mãn: ( 2 x + x + )( 2
1 y + y +1) = 2. Tính giá trị biểu thức 2 2
Q = x y +1 + y x +1.
b) Cho x, y là các số thực dương thỏa mãn: 2 2
4x + 4y +17xy + 5x + 5y ≥ 1. Tính giá trị nhỏ nhất của biểu thức 2 2
P =17x +17y +16x .y --------Hết--------
LỜI GIẢI ĐỀ TUYỂN SINH VÀO 10 CHUYÊN TỈNH SƠN LA
NĂM HỌC 2022 – 2023
Câu 1. (2,0 điểm)  2 x + 5   3
Cho biểu thức: A   : 1  = + −
(x ≥ 0 ; x ≠ 1 ; x ≠   4)  x +1
x − x − 2   4 − x  a) Rút gọn biểu thức . A
b) Tìm các giá trị nguyên của x để A đạt giá trị nguyên. Lời giải: x 0  2 x + 5  ≥  4 − x − 3 a) Với  A    ⇒ = + x ≠ x +1  (   
x + )1( x − 2) : 1 ; 4   4 − x  
( x − )+ x+     ( x x x x x + − + + − )2 2 2 5 1 1 2 1 1  x − 4 A  ⇒ = ( = = ⋅      
x + )1( x − 2) : − x  ( x + )1( x − 2) : 4
 x − 4  ( x + )1( x − 2)  x −1 
( x + )1 ( x −2)( x +2) x +2 A (   ⇒ = ⋅ =
x − 2)  ( x − )1( x +  )1  x −1  x + 2 Vậy A= x −1 x + 2 x −1+ 3 3 b) Ta có: A= = =1+ x −1 x −1 x −1 3
Để A đạt giá trị nguyên
∈  ⇒ x −1∈U (3) = {± 1 ; ± } 3 x −1 Lập bảng: x −1 - 1 1 - 3 3 x 0 2 - 2 4 x 0 4 16 TM Loại Loại TM Vậy x ∈ {0; } 16 ⇒ A ∈ . 
Câu 2. (2,0 điểm)
y − 2x −1 = 0
a) Giải hệ phương trình:  2 2
4x − 3xy + y =1 b) Giải phương trình: 2 x + x + = ( 2 2 7 3 x + ) 1 (x + 3) Lời giải:
y − 2x −1 = 0 y = 2x +1 ( ) 1 a) Ta có:  ⇔ 2 2  2 2
4x − 3xy + y = 1
4x − 3xy + y = 1  (2)
Thay (1) vào (2) ta được: 2
x − x( x + ) + ( x + )2 2 2 2 4 3 2 1
2 1 =1 ⇔ 4x − 6x − 3x + 4x + 4x +1 =1 x = 0 2 2x x 0 x(2x ) 1 0  ⇔ + = ⇔ + = ⇔ −1 x =  2
Với x = 0 ⇒ y = 1 Với − 1 x = ⇒ y = 0 2 Vậy (x y ) ( )  −1 ; 0 ; 1 ; ; 0 =  2    b) ĐKXĐ: x ≥ − 3 2
⇒ PT ⇔ x + + (x + ) = ( 2 1 2 3 3 x + ) 1 (x + 3) (*) a = x +3 Đặt: 
(a ≥ 0 ; b > 0) 2 b  = x +1 ⇒ ( ) 2 2 2 2 2 2
* ⇔ b + 2a = 3ab ⇔ 2a −3ab + b = 0 ⇔ 2a − 2ab − ab + b = 0 ⇔ 2a(a −b) −b(a −b) = 0 ( − )(  − =  = a − b) a b 0 a b a b 2 = 0 ⇔ ⇔  2a b 0  − = 2a = b x = 1 − TH1: Nếu 2 2 2
a = b ⇔ x + 3 = x +1 ⇔ x +1 = x + 3 ⇔ x − x − 2 = 0 ⇔  (TM ) x = 2 x = 2 + 15 TH2: Nếu 2 2
2a = b ⇔ 2 x + 3 = x +1 ⇔ x +1 = 4(x + 3) 2
⇔ x − 4x −11 = 0 ⇔  (TM ) x = 2 − 15 Vậy S = { 1; − 2; 2 ± 15}
Câu 3. (2,0 điểm)
a) Tìm giá trị của tham số k để đường thẳng (d : y = −x + 2 cắt đường thẳng 1 )
(d : y = 2x +3− k 2 )
tại một điểm nằm trên trục hoành.
b) Trong mặt phẳng tọa độ Oxy , cho parabol (P) 2
: y = x và đường thẳng
(d): y = 2mx − m +1 (Với m là tham số). Tìm tất cả các giá trị của m để (d ) cắt (P) tại hai điểm
phân biệt có hoành độ x ; x thỏa mãn: x − x > 3. 1 2 1 2 Lời giải:
a) Giả sử A(x
y là giao điểm của đường thẳng (d : y = −x + 2 và (d : y = 2x + 3− k 2 ) 1 ) A ; A )  y =  y =  y = A 0 A 0 A 0
Do: A nằm trên trục hoành và A ∈ d ⇒  ⇒  ⇒  ⇒ A 2 ; 0 1 ( ) y = −x + = −  x + x =  A A 2 0 A 2 A 2
Mà: A ∈ d ⇒ 0 = 2.2 + 3− k ⇒ k = 7 2
Vậy k = 7 thỏa mãn yêu cầu bài toán
b) Xét phương trình hoành độ giao điểm giữa (P) và (d ): 2 2
x = 2mx − m +1 ⇔ x − 2mx + m −1 = 0 (a =1 ; b = 2
− m ; c = m − ) 1 2 Ta có: 2
∆ = b − ac = (−m)2 − (m − ) 2 2 1 1 3  1  3 ' ' 1.
1 = m − m +1 = m − 2. . m + + = m − + >0 ∀   m 2 4 4  2  4
⇒ (P) luôn cắt (d ) tại hai điểm phân biệt với ∀m  −b x + x = = 2m  1 2 Theo Vi-Et ta có:  a  c
x x = = m −1 1 2  a Mà: 2
x − x > 3 ⇔ x − x > ( 3)2 2 2
⇔ x + x − 2x x > 3 ⇔ x + x − 4x x > 3 * 1 2 1 2 1 2 1 2 ( 1 2)2 1 2 ( )
Thay vào (*) ta được: ( m)2 − (m − ) 2 >
⇔ m − m + > ⇔( m − )2 1 2 4 1 3 4 4 1 0 2 1 > 0 ⇔ m ≠ 2 Vậy 1
m ≠ thỏa mãn yêu cầu bài toán 2
Câu 4. (3,0 điểm)
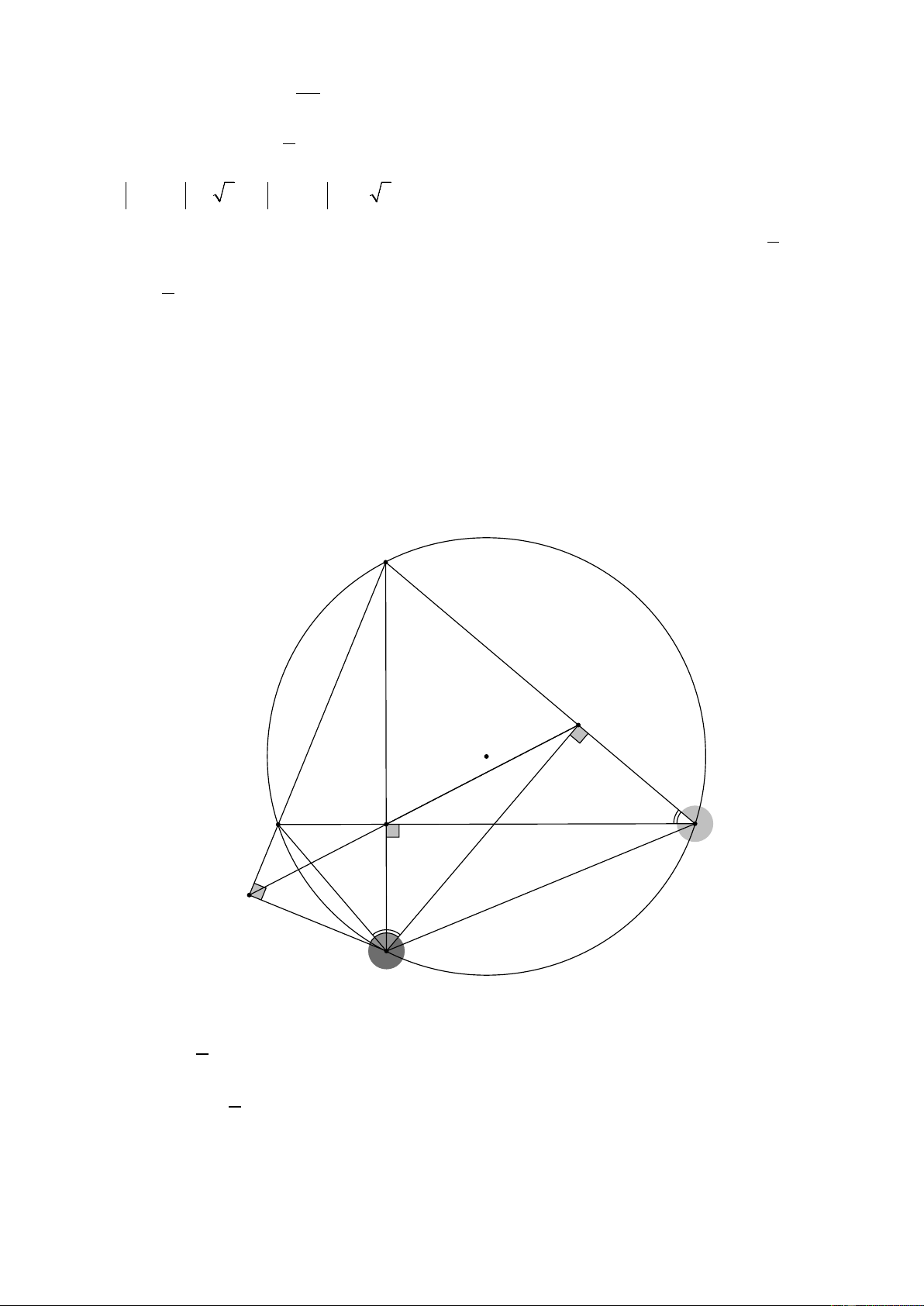
Cho ∆ ABC có ba góc nhọn ( AB > AC) nội tiếp đường tròn (O ; R). Đường cao AH của
∆ ABC cắt đường tròn (O ; R) tại điểm thứ hai là D . Kẻ DM ⊥ AB tại M.
a) Chứng minh tứ giác BMHD nội tiếp được đường tròn và DA là tia phân giác của  MDC .
b) Từ D kẻ DN ⊥ AC tại N. Chứng minh ba điểm M , H, N thẳng hàng. c) Cho 2 2 2 2
P = AB + AC + BD + CD . Tính giá trị biểu thức P theo R . Lời giải: A M O H 2 2 C 2 1 1 B 1 N 1 2 4 3 D a) Ta có:  = 
DHB DMB = 90 ⇒  DHMB nội tiếp ⇒  =  1 =  D B HM 2 2 2 1 Mà: ⇒  =  =  D B AC 1 2 2 ⇒  =  =  D D B ⇒ 1 2 ( 2 ) đpcm
b) Ta có:  ABDC nội tiếp  =  C ABD 1
(góc ngoài tứ giác nội tiếp)
⇒ ∆ NCD ≈ ∆ MBD (g.g) ⇒  =  D D 4 3 (hai góc tương ứng)
Mà:  NCHD nội tiếp (Vì:  =  N H = 90) ⇒  =  D H 4 1 1 Mặt khác:  =  =  D H
MB ⇒ H = H 3 2   2 1 2
Do: C, H, B thẳng hàng nên ta có đpcm. c)
Câu 5. (1,0 điểm)
a) Cho x, y là các số thực dương thỏa mãn: ( 2 x + x + )( 2
1 y + y +1) = 2. Tính giá trị biểu thức 2 2
Q = x y +1 + y x +1.
b) Cho x, y là các số thực dương thỏa mãn: 2 2
4x + 4y +17xy + 5x + 5y ≥ 1. Tính giá trị nhỏ nhất của biểu thức 2 2
P =17x +17y +16x .y Lời giải: a) Ta có: ( 2 x + x + )( 2
y + y + ) = ⇔ ( 2 x + x + )( 2 y + y + )( 2
− x + x + ) = ( 2 1 1 2 1 1
1 2 − x + x +1) ⇔ ( 2 y + y + ) 2 1 = 2
− x + 2 x +1 ( ) 1 TT ( 2 x + x + ) 2 : 1 = 2
− y + 2 y +1 (2)
Trừ (1) với (2) vế theo vế: 2 2 2 2
x − y + x +1 − y +1 = 2
− y + 2x + 2 y +1 − 2 x +1  +  ⇔ ( − ) x y x y −3( 3 2 2
x +1 − y +1) = 0 ⇔ (x − y) ( ) 1−  = 0  2 2 x 1 y 1  + + +   x = y ⇔  2 2
 x +1 + y +1 −3x −3y = 0 x < 2 TH1: Nếu 2 2
x = y ⇔ x + x +1 = 2 ⇔ x +1 = 2 − x ⇔  2 2
x +1= 2 − 2 2x + x 1 2 3 ⇔ x = = = y ⇒ Q = 2 2 4 4 TH2: Nếu 2 2
x +1 + y +1 −3x −3y = 0 --------Hết--------
Document Outline

• de-tuyen-sinh-lop-10-mon-toan-chuyen-nam-2022-2023-truong-chuyen-son-la
• 51. ĐIỆN BIÊN