Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2023 – 2024 sở GD&ĐT An Giang
Giới thiệu đến quý thầy, cô giáo và các em học sinh đề chính thức kỳ thi tuyển sinh vào lớp 10 THPT môn Toán (chuyên) năm học 2023 – 2024 sở Giáo dục và Đào tạo tỉnh An Giang; kỳ thi được diễn ra vào ngày 03 tháng 06 năm 2023. Mời bạn đọc đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT AN GIANG Năm học 2023-2024
Khóa ngày 03/6/2023 ĐỀ CHÍNH THỨC
Môn thi: TOÁN CHUYÊN
(Đề thi gồm có 01 trang)
Thời gian làm bài 150 phút, không kể thời gian phát đề Câu 1. (1,0 điểm) Thực hiện phép tính √7 + 1 2√14 𝐴 = − + √7 − 2√2. 3 − 2√2 √2 − 1 Câu 2. (1,0 điểm) Giải hệ phương trình 𝑥 + √3𝑦 = 6 − 2√3 { . 𝑥 + 𝑦 = 2 Câu 3. (1,0 điểm)
Phương trình 𝑥2 + 𝑎𝑥 + 𝑏 = 0 (với 𝑎; 𝑏 là các số nguyên) có một nghiệm là
5 + √21 . Tính nghiệm còn lại. Câu 4. (1,0 điểm)
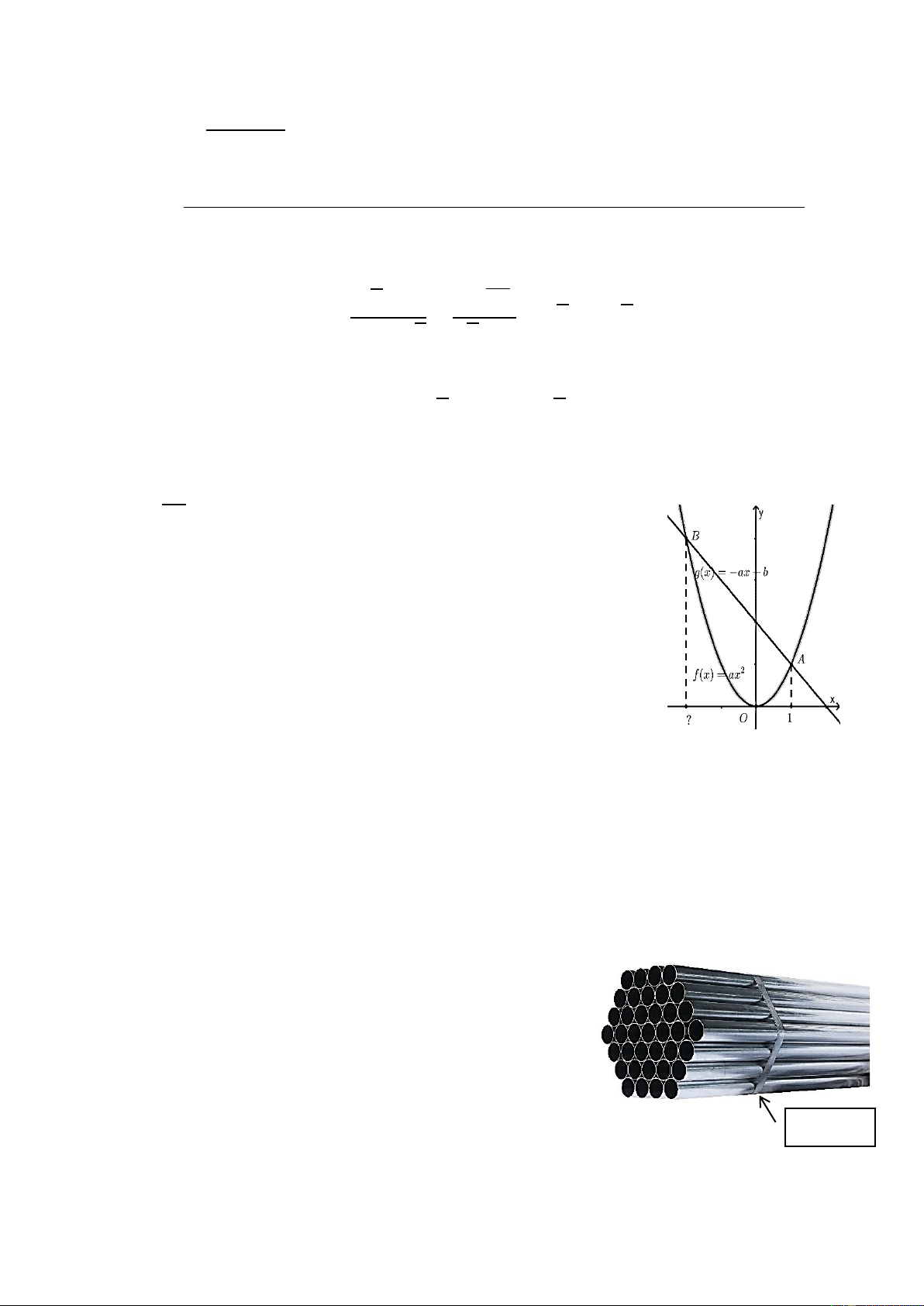
Hình vẽ bên là đồ thị của hai hàm số 𝑓(𝑥) = 𝑎𝑥2 và
𝑔(𝑥) = −𝑎𝑥 + 𝑏 (𝑎; 𝑏 là các số thực), điểm chung thứ nhất
có hoành độ bằng 1. Tìm hoành độ của điểm chung thứ hai của hai đồ thị. Câu 5. (1,5 điểm)
Cho 𝑥3 + 𝑦3 = 189 và (𝑥 + 𝑦)(𝑥 + 1)(𝑦 + 1) = 270 . Tính 𝑥 + 𝑦. Câu 6. (3,5 điểm)
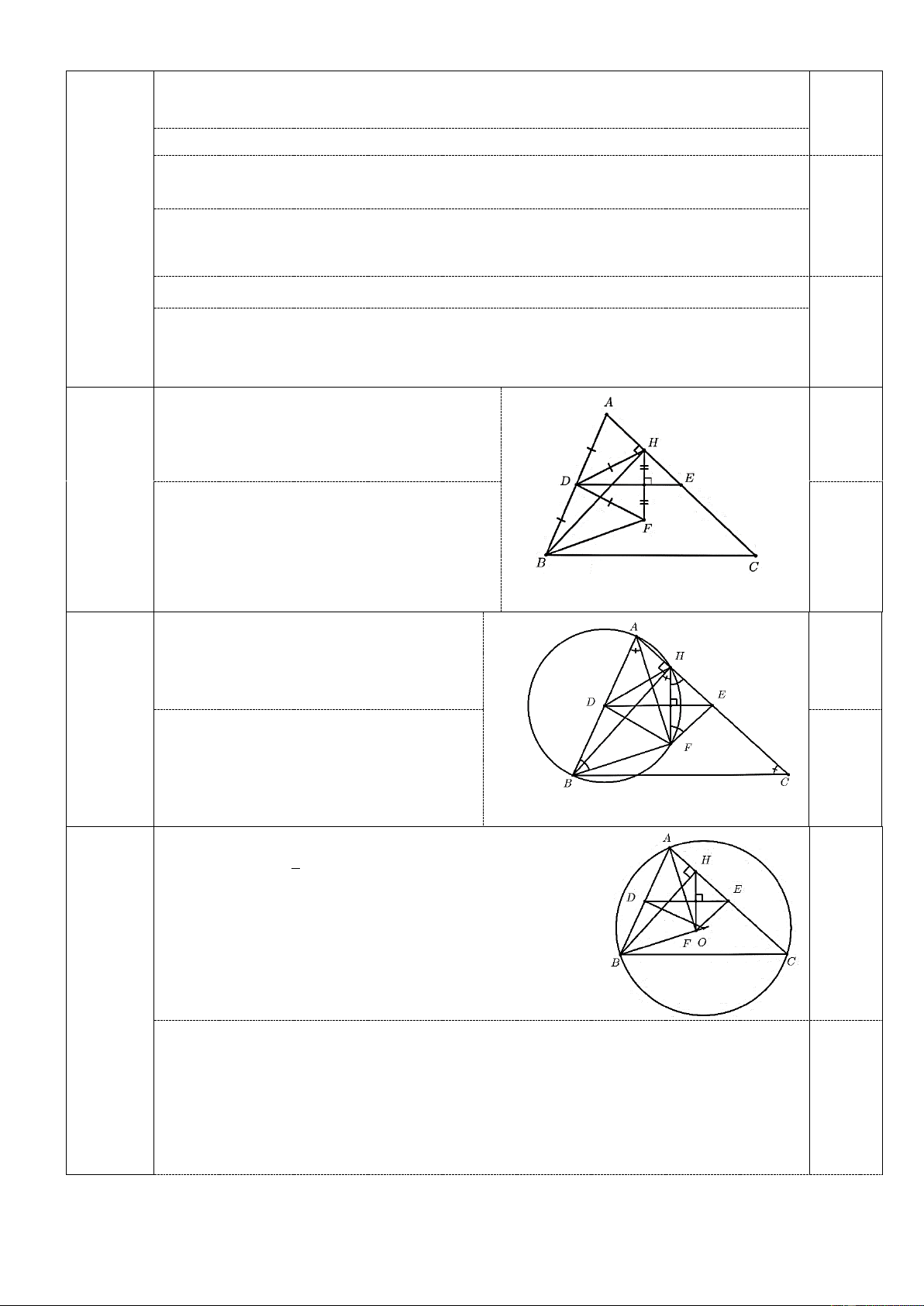
Cho tam giác 𝐴𝐵𝐶 có ba góc đều nhọn, 𝐵𝐻 là đường cao kẻ từ 𝐵 (𝐻 ∈ 𝐴𝐶).
Gọi 𝐷, 𝐸 lần lượt là trung điểm của 𝐴𝐵 và 𝐴𝐶, 𝐹 là điểm đối xứng của điểm 𝐻 qua 𝐷𝐸.
a. Chứng minh rằng tứ giác 𝐴𝐵𝐹𝐻 nội tiếp. b. Chứng minh 𝐹𝐵𝐴 ̂ = 𝐸𝐹𝐻 ̂ .
c. Chứng minh rằng 𝐵𝐹 đi qua tâm đường tròn ngoại tiếp tam giác 𝐴𝐵𝐶. Câu 7. (1,0 điểm)
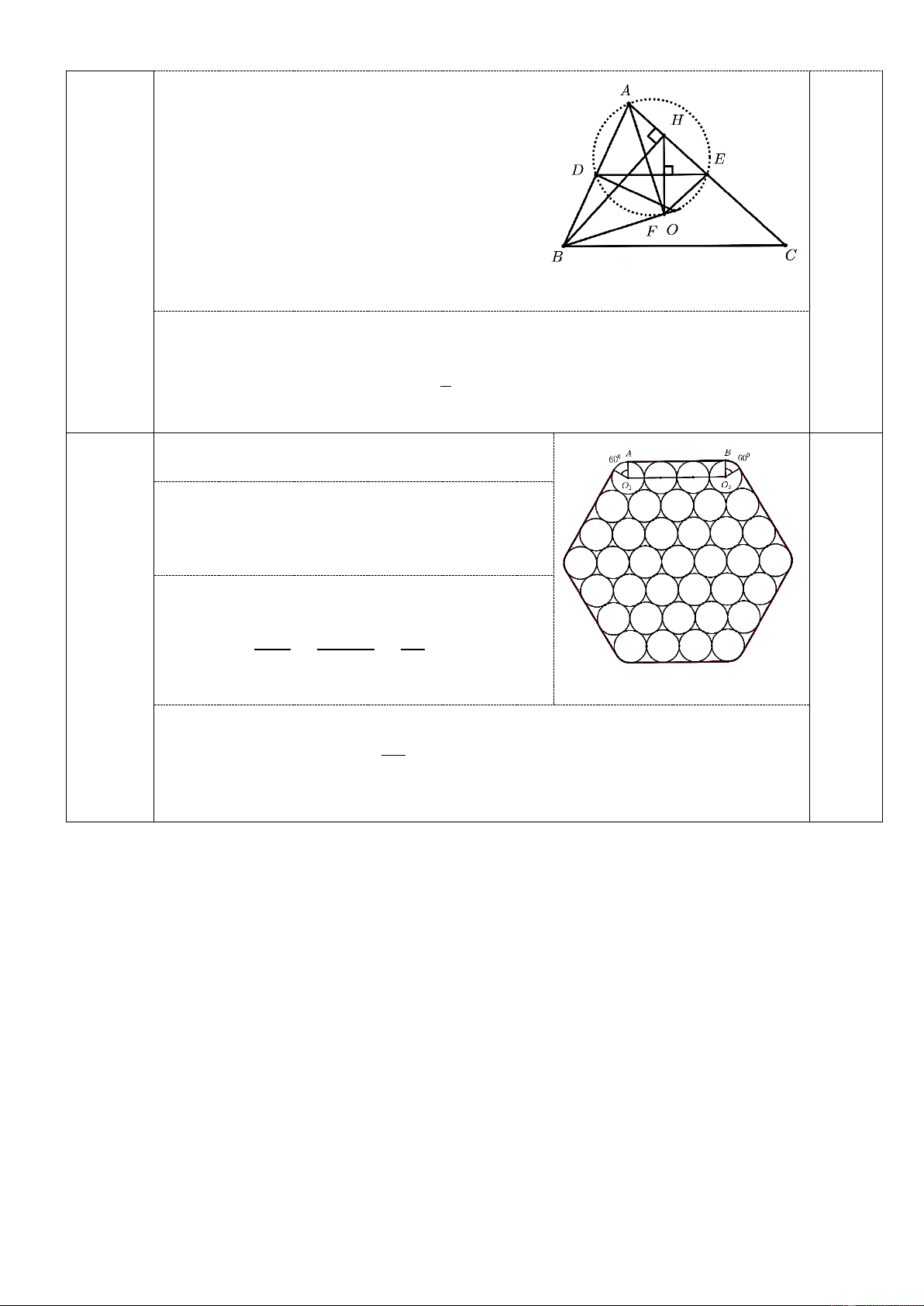
Một nhà máy sản xuất ống thép khi xuất xưởng
các ống thép được bó lại tạo thành khối gồm 37 ống
như hình vẽ. Biết các ống có dạng hình trụ đường
kính đáy bằng nhau và bằng 10cm. Tính độ dài của
một sợi dây đai để buột các ống thép lại với nhau. Dây đai ------Hết------
Số báo danh:. . . . . . . . . . . . . . . . . . . . . .; Phòng thi:. . . . . .
SỞ GIÁO DỤC ĐÀO TẠO
ĐÁP ÁN ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT AN GIANG Năm học 2023-2024 Khóa ngày: 03/6/2023 MÔN: TOÁN CHUYÊN Câu Lược giải Điểm √7 + 1 2√14 𝐴 = − + √7 − 2√2 3 − 2√2 √2 − 1 0,25 √7 + 1 (√7 + 1)(3 + 2√2) + = = 3√7 + 2√14 + 3 + 2√2 Câu1 3 − 2√2 9 − 8 (1,0đ) 2√14 +
= 2√14(√2 + 1) = 4√7 + 2√14 0,25 √2 − 1
⇒ 𝐴 = 3√7 + 2√14 + 3 + 2√2 − (4√7 + 2√14) + √7 − 2√2 = 3 0,5 Vậy 𝐴 = 3. ( {𝑥 + √3𝑦 = 6 − 2√3 √3 − 1)𝑦 = 4 − 2√3
⇔ {√3𝑦 − 𝑦 = 4 − 2√3 ⇔ { 𝑥 + 𝑦 = 2 𝑥 + 𝑦 = 2 𝑥 + 𝑦 = 2 0,5 Câu2 4 − 2√3 (4 − 2√3)(√3 + 1) ⇒ 𝑦 = = = −1 + √3 (1,0đ) √3 − 1 2
⇒ 𝑥 = 2 − 𝑦 = 2 − (−1 + √3) = 3 − √3 0,5
Hệ có nghiệm 𝑥 = 3 − √3; 𝑦 = −1 + √3.
Phương trình 𝑥2 + 𝑎𝑥 + 𝑏 = 0 (với 𝑎; 𝑏 là các số nguyên) có một nghiệm là
5 + √21 . Thay 𝑥 = 5 + √21 vào phương trình ta được 2
(5 + √21) + 𝑎(5 + √21) + 𝑏 = 0 0,5
⇔ 25 + 10√21 + 21 + 5𝑎 + 𝑎√21 + 𝑏 = 0
⇔ (10 + 𝑎)√21 + 5𝑎 + 𝑏 + 46 = 0 Câu3 (1,0đ)
Vì 𝑎, 𝑏 là các số nguyên nên 10 + 𝑎 = 0 𝑎 = −10 𝑎 = −10 { ⇔ { ⇔ { 5𝑎 + 𝑏 + 46 = 0 −50 + 𝑏 + 46 = 0 𝑏 = 4 0,5
Phương trình trở thành 𝑥2 − 10𝑥 + 4 = 0
do 𝑥1 + 𝑥2 = 10 ⇒ 𝑥2 = 10 − 𝑥1 = 10 − (5 + √21) = 5 − √21
Vậy nghiệm còn lại là 5 − √21.
Phương trình hoành độ giao điểm của hai đồ thị
là 𝑎𝑥2 = −𝑎𝑥 + 𝑏
⇔ 𝑎𝑥2 + 𝑎𝑥 − 𝑏 = 0
Dựa vào hình vẽ phương trình có một nghiệm Câu4 𝑥 (1,0đ) 1 = 1 , nghiệm còn lại 1,0 𝑎 𝑥 = −1 1 + 𝑥2 = − 𝑎
1 + 𝑥2 = −1 ⇔ 𝑥2 = −2
Vậy giao điểm thứ hai có hoành độ 𝑥 = −2. 2
Cho 𝑥3 + 𝑦3 = 189 và (𝑥 + 𝑦)(𝑥 + 1)(𝑦 + 1) = 270 . Tính 𝑥 + 𝑦.
Đặt 𝑆 = 𝑥 + 𝑦; 𝑃 = 𝑥𝑦 ta được 0,5
𝑥3 + 𝑦3 = (𝑥 + 𝑦)(𝑥2 − 𝑥𝑦 + 𝑦2) = 𝑆(𝑆2 − 3𝑃) = 𝑆3 − 3𝑆𝑃
(𝑥 + 𝑦)(𝑥 + 1)(𝑦 + 1) = (𝑥 + 𝑦)(𝑥𝑦 + 𝑥 + 𝑦 + 1) = 𝑆(𝑆 + 𝑃 + 1) = 𝑆2 + 𝑆𝑃 + 𝑆 Câu5 0,5 Theo giả thiết ta có (1,5đ) { 𝑆3 − 3𝑆𝑃 = 189 𝑆2 + 𝑆𝑃 + 𝑆 = 270
⇒ 𝑆3 + 3𝑆2 + 3𝑆 = 999
⇔ 𝑆3 + 3𝑆2 + 3𝑆 + 1 = 1000 0,5
⇔ (𝑆 + 1)3 = 1000 ⇒ 𝑆 + 1 = 10 ⇔ 𝑆 = 9 Vậy 𝑥 + 𝑦 = 9.
Ta có tam giác 𝐴𝐻𝐵 vuông tại 𝐻, 𝐷 là
trung điểm 𝐴𝐵 nên 𝐴𝐷 = 𝐷𝐵 = 𝐷𝐻 0,5
(tính chất trung tuyến của tam giác vuông). Câu6a
𝐷𝐻 = 𝐷𝐹 (do 𝐻 và 𝐹 đối xứng nhau (1,5đ)
qua 𝐷𝐸) ⇒ 𝐷𝐴 = 𝐷𝐻 = 𝐷𝐹 = 𝐷𝐵.
Vậy tứ giác 𝐴𝐵𝐹𝐻 nội tiếp trong đường 0,5 tròn có tâm 𝐷. (Hình vẽ 0,5đ)
Tứ giác 𝐴𝐵𝐹𝐻 nội tiếp trong đường tròn có tâm 𝐷 0,5 Suy ra 𝐹𝐵𝐴 ̂ = 𝐹𝐻𝐸 ̂ (cùng bù với 𝐹𝐻𝐴 ̂ ) Câu6b (1,0đ) 𝐸𝐹𝐻 ̂ = 𝐹𝐻𝐸
̂ (do 𝐹, 𝐻 đối xứng qua 𝐷𝐸) 0,5 ⇒ 𝐹𝐵𝐴 ̂ = 𝐸𝐹𝐻 ̂
Giả sử 𝑂 là tâm đường tròn ngoại tiếp tam giác 𝐴𝐵𝐶 khi đó 1 𝐴𝐶𝐵 ̂ = 𝐴𝑂𝐵
̂ và ngược lại, do 𝐷 là trung 2 điểm 𝐴𝐵 nên 𝐴𝐶𝐵 ̂ = 𝐷𝑂𝐵 ̂ = 900 − 𝑂𝐵𝐴 ̂ 0,5
Do đó ta chỉ cần chứng minh 𝐴𝐶𝐵 ̂ = 900 − 𝐹𝐵𝐴 ̂ Câu6c thì 𝐵𝐹 đi qua 𝑂. (1,0đ) Thật vậy 𝐴𝐶𝐵 ̂ = 𝐴𝐸𝐷
̂ (do 𝐸𝐷 song song 𝐶𝐵) 𝐴𝐸𝐷 ̂ = 900 − 𝐸𝐻𝐹 ̂ = 900 − 𝐸𝐹𝐻 ̂ = 900 − 𝐹𝐵𝐴 ̂ 0,5 (chứng minh câu b) Vậy 𝐴𝐶𝐵 ̂ = 900 − 𝐹𝐵𝐴
̂. Điều phải chứng minh,
hay đường thẳng 𝐵𝐹 đi qua tâm 𝑂 của đường tròn ngoại tiếp tam giác 𝐴𝐵𝐶. 3 Cách khác
Gọi 𝑂 là tâm đường tròn ngoại tiếp tam giác 𝐴𝐵𝐶
Tứ giác 𝐴𝐷𝑂𝐸 nội tiếp trong đường tròn do 𝑂𝐸𝐴 ̂ = 𝑂𝐷𝐴 ̂ = 900
Mà 𝐴𝐷 = 𝐷𝐻 = 𝐷𝐵 nên 𝐵𝐴𝐶 ̂ = 𝐷𝐻𝐴 ̂ = 1800 − 𝐷𝐻𝐸 ̂ = 1800 − 𝐷𝐹𝐸 ̂
Vậy tứ giác 𝐴𝐷𝐹𝑂 nội tiếp hay các điểm
𝐴, 𝐷, 𝐹, 𝑂, 𝐸 cùng nằm trên một đường tròn. ⇒ 𝐶̂ = 𝐷𝐸𝐴 ̂ = 𝐷𝐸𝐹 ̂ = 𝐷𝑂𝐹 ̂
Vì 𝑂 là tâm đường tròn ngoại tiếp tam giác nên 1 𝐶̂ = 𝐴𝑂𝐵 ̂ = 𝐷𝑂𝐵 ̂ 2 Vậy 𝐷𝑂𝐹 ̂ = 𝐷𝑂𝐵
̂ hay 𝐵𝐹 đi qua tâm 𝑂 đường tròn ngoại tiếp tam giác 𝐴𝐵𝐶.
Dây đai xem là hình giới hạn bởi 6 đoạn thẳng
và 6 cung tròn bằng nhau như hình vẽ.
Độ dài mỗi đoạn chính là khoảng cách giữa
hai tâm đường tròn biên gồm 4 đường tròn tiếp
xúc nhau và tiếp xúc với dây đai.
Độ dài mỗi cạnh: 3 × 10 = 30cm
Mỗi cung tròn có số đo cung bằng 600, độ dài Câu7 mỗi cung bằng: 1,0 (1,0đ) 𝜋𝑅𝑛 𝜋. 5.60 5𝜋 = = cm 180 180 3 Độ dài dây đai là: 5𝜋 30 × 6 +
× 6 = 180 + 10𝜋 ≈ 211,4cm. 3
(nếu học sinh xem dây đai là lục giác đều độ dài 6 cạnh, mỗi cạnh 40cm
hoặc 30cm thì điểm tối đa là 0,25)
Lưu ý: - Thí sinh làm cách khác đúng vẫn cho điểm tối đa.
- Điểm tổng toàn bài giữ nguyên không làm tròn. 4