

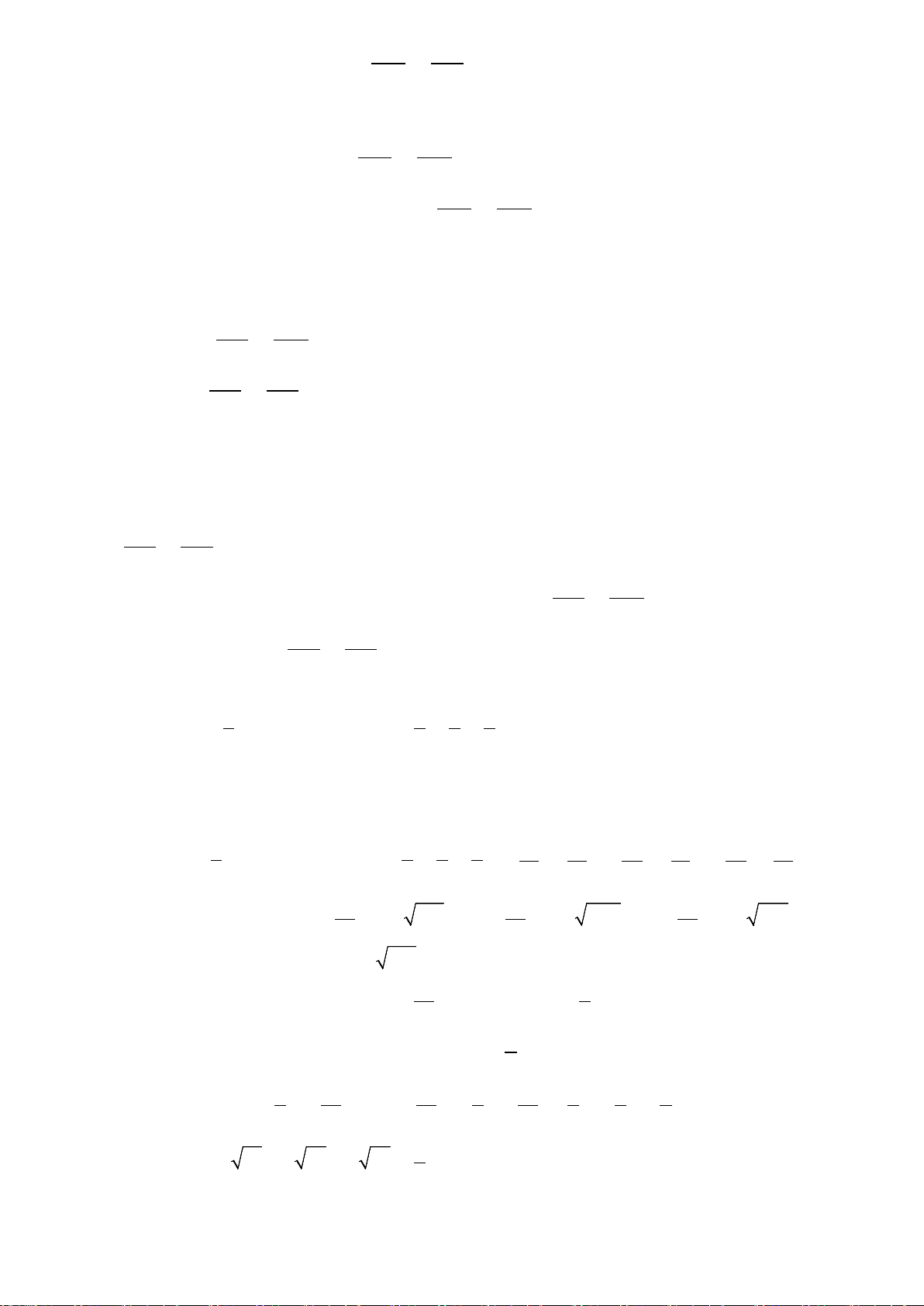
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH.
KỲ THI TUYỂN SINH LỚP 10 NĂM HỌC 2023 – 2024
Ngày thi: 02 tháng 06 năm 2023
Môn thi: TOÁN (chuyên)
Thời gian: 150 phút (Không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề thi có 1 trang, thí sinh không phải chép đề vào giấy thi)
Câu 1: (1 điểm) Tính giá trị của biểu thức T 13 4 3 13 4 3 .
Câu 2: (1 điểm) Cho hai đường thẳng d : y ax 5 và d : y 3x b 2 . Tìm a,b biết d 1 2 1
và d cùng đi qua điểm M(2;3). 2
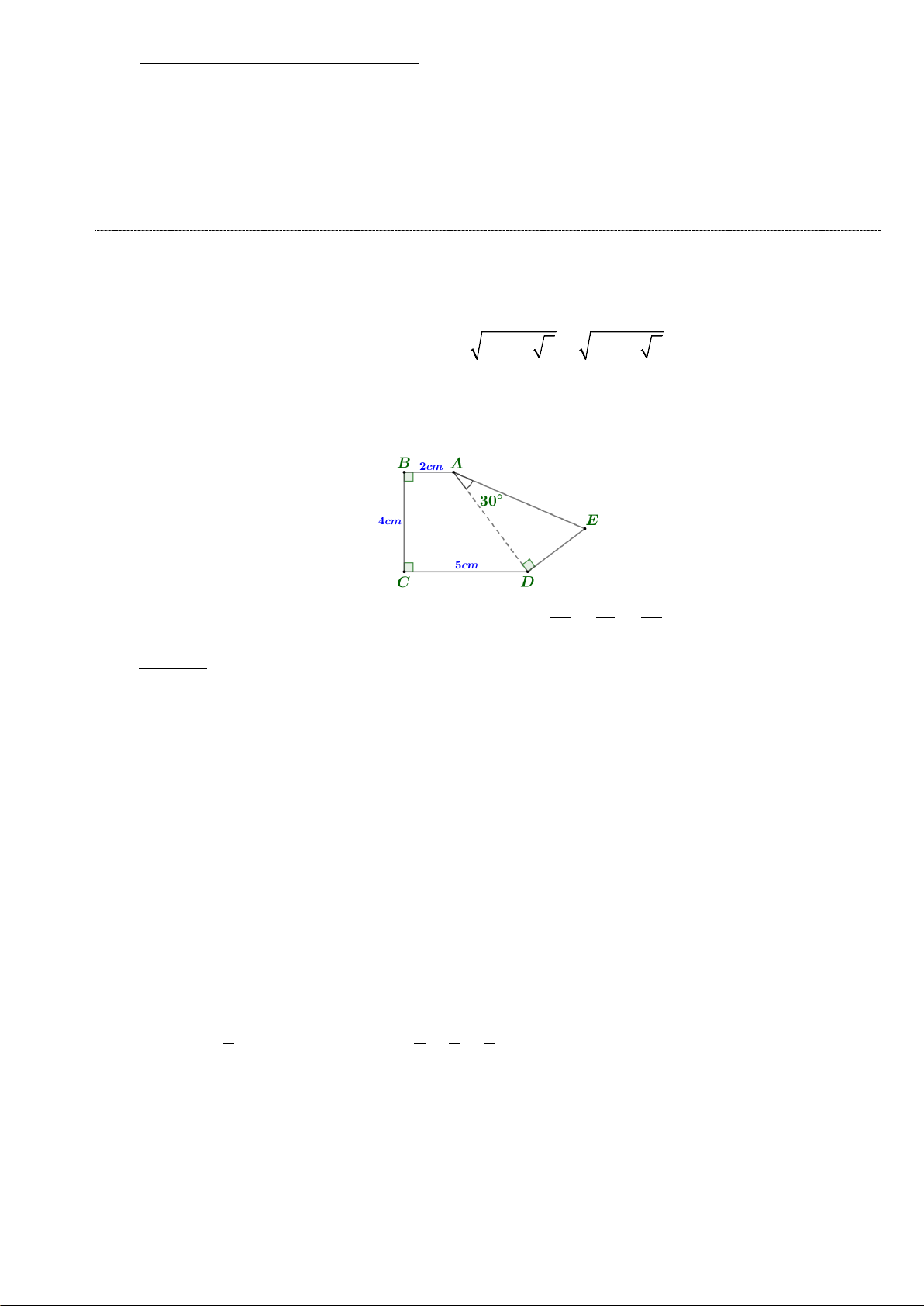
Câu 3: (1 điểm) Cho hình phẳng có số liệu như hình vẽ. Tính độ dài đoạn thẳng AE .
Câu 4: (1 điểm) Cho a b c a, ,
b c là ba số thực khác 0 thỏa mãn 2 3
. Tính giá trị của biểụ thức b c 6a 4ac cb P . bc 2ab
Câu 5: (1 điểm) Tìm nghiệm nguyên của phương trình 2 2 2
(x y) 2y (x 1) (y 2) 9 0.
Câu 6: (1 điểm) Cho parabol 2
(P) : y 2x và đường thẳng (d) : y (7 m)x 3m 3 . Tìm các
giá trị nguyên âm của m để (P) cắt (d) tại hai điểm phân biệt có hoành độ nhỏ hơn 4.
Câu 7: (1 điểm) Cho đường tròn (O) đường kính AB . Trên (O) lấy hai điểm C,D nằm khác phía
đối với AB và CD không đi qua O . Gọi E là giao điểm của AC và ,
BD F là giao điểm của AD
và BC,I là trung điểm đoạn thẳng EF . Chứng minh IC là tiếp tuyến của (O) .
Câu 8: (2 điểm) Cho đường tròn (O) và điểm M nằm ngoài (O) , vẽ tiếp tuyến MA và cát tuyến
MBC không đi qua O(MB MC ) . Gọi H là hình chiếu vuông góc của A trên MO .
a) (1,0 điểm) Chứng minh: Tứ giác BHOC nội tiếp.
b) (1,0 điểm) Vẽ đường thẳng qua B song song với AC cắt các đường thẳng , MA AH lần lượt
tại K,I . Chứng minh KB BI .
Câu 9: (1 điểm) Cho a, ,
b c là các số thực dương thỏa mãn a b c 6. Tìm giá trị nhỏ nhất của biểu thức 1 5 6 7
M (19a 22b 25c) 2 . 6 a b c
…………. HẾT ………….
Giám thị không giải thích gì thêm.
Họ và tên thí sinh: ………………………………………….. Số báo danh: ………………..
Chữ ký của giám thị 1: ……………………. Chữ ký của giám thị 2: ……………………… HƯỚNG DẪN GIẢI
Câu 1: (1 điểm) Tính giá trị của biểu thức T 13 4 3 13 4 3 . Lời giải
▪ Ta có: T 13 4 3 13 4 3 12 2.2 3.1 1 12 2.2 3.1 1 2 2 2 3 1 2 3
1 2 3 1 2 3 1 2 3 1 2 3 1 2 .
Câu 2: (1 điểm) Cho hai đường thẳng d : y ax 5 và d : y 3x b 2 . Tìm a,b biết d 1 2 1
và d cùng đi qua điểm M(2;3). 2 Lời giải 2 a 5 3 a 4
▪ Do d và d cùng đi qua điểm M(2;3) nên ta có: . 2 1 6
b 2 3 b 7
▪ Vậy a 4;b 7 .
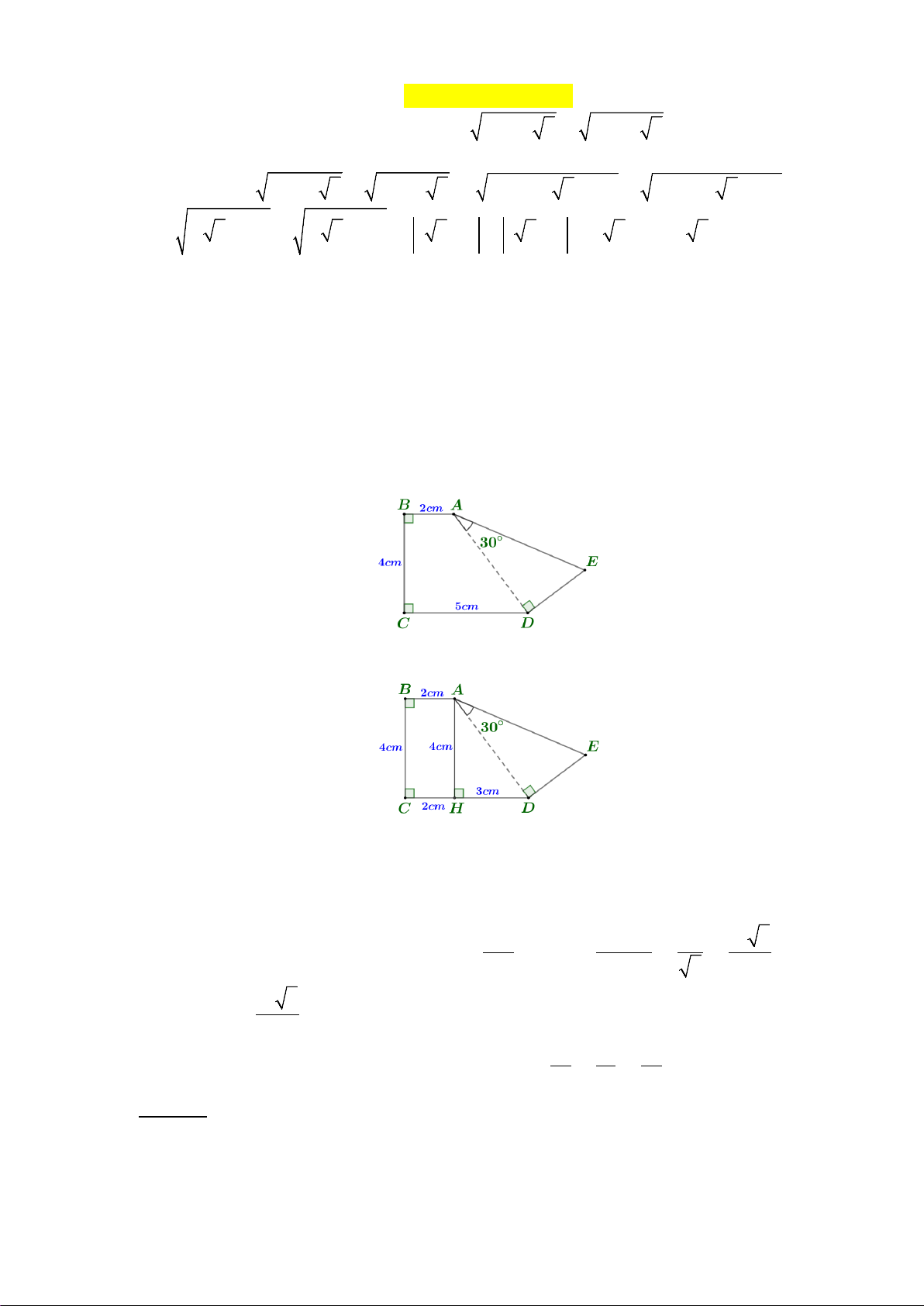
Câu 3: (1 điểm) Cho hình phẳng có số liệu như hình vẽ. Tính độ dài đoạn thẳng AE . Lời giải
▪ Kẻ AH CD .
▪ Suy ra: ABCH là hình chữ nhật AH 4 cm;HD CD CH 3 cm . ▪ Xét AHD
H 90 có: 2 2 2 2 2
AD AH HD 4 3 25 AD 5 cm . ▪ Xét AD AD A
DE ADE 90 có: 10 10 3 cos 30 AE . AE cos 30 3 3 ▪ Vậy 10 3 AE . 3
Câu 4: (1 điểm) Cho a b c a, ,
b c là ba số thực khác 0 thỏa mãn 2 3
. Tính giá trị của biểụ thức b c 6a 4ac cb P . bc 2ab Lời giải 2 a bt ▪ Đặt: 2a 3b c c 2 t b
t 2at 3
2a 2at t 1. b c 6a 3
c 6at b 2a ▪ Suy ra: . c 6a ▪ 4ac cb
4a.6a 6a.2a 12 3 P . bc 2ab
2a.6a 2a.2a 16 4
Câu 5: (1 điểm) Tìm nghiệm nguyên của phương trình 2 2 2
(x y) 2y (x 1) (y 2) 9 0. Lời giải 2 2 2
(x y) 2y (x 1) (y ) 2 9 0 2 2 2 2 2
x y 2xy 2xy 2y y 4y 4 9 0 2
x 4 2x 2
y y 4 2 y y 1
x 2x 2 2 2
y yx 2 1 x 2 2
x 2 2y 2y 1 x 1 x 2 1 x 1 ▪ TH1:
y 1 1;1 , 1;2 . 2 2 x
2 2y 2y 1 2
y 2y 4 0 y 2 x 3 x 2 1 x 3 ▪ TH2:
y 1 3;1 , 3;2 . 2 2 x
2 2y 2y 1 2
y 2y 4 0 y 2
Câu 6: (1 điểm) Cho parabol 2
(P) : y 2x và đường thẳng (d) : y (7 m)x 3m 3 . Tìm các
giá trị nguyên âm của m để (P) cắt (d) tại hai điểm phân biệt có hoành độ nhỏ hơn 4. Lời giải
▪ Phương trình hoành độ giao điểm của 2
(P) : y 2x và (d) : y (7 m)x 3m 3 là: 2
2x 7 mx 3m 3 2
2x 7 mx 3 3m 0
m2 m 2 7 4.2. 3 3
m 14m 49 24 24m m m m 2 2 10 25
5 0, m .
▪ Để (P) cắt (d) tại hai điểm phân biệt thì 0 m 5 .
▪ Khi đó phương trình có hai nghiệm phân biệt:
7 m m 5 2m 2 m 1 x ; 1 4 4 2
7 m m 5 12 x 3 . 2 4 4 ▪ Yêu cầu bài toán m 1 4 m 1 8 m
7 m 7 . 2
▪ Vậy tập các giá trị nguyên âm thoả yêu cầu bài toán của m là: 6;4;3;2; 1 .
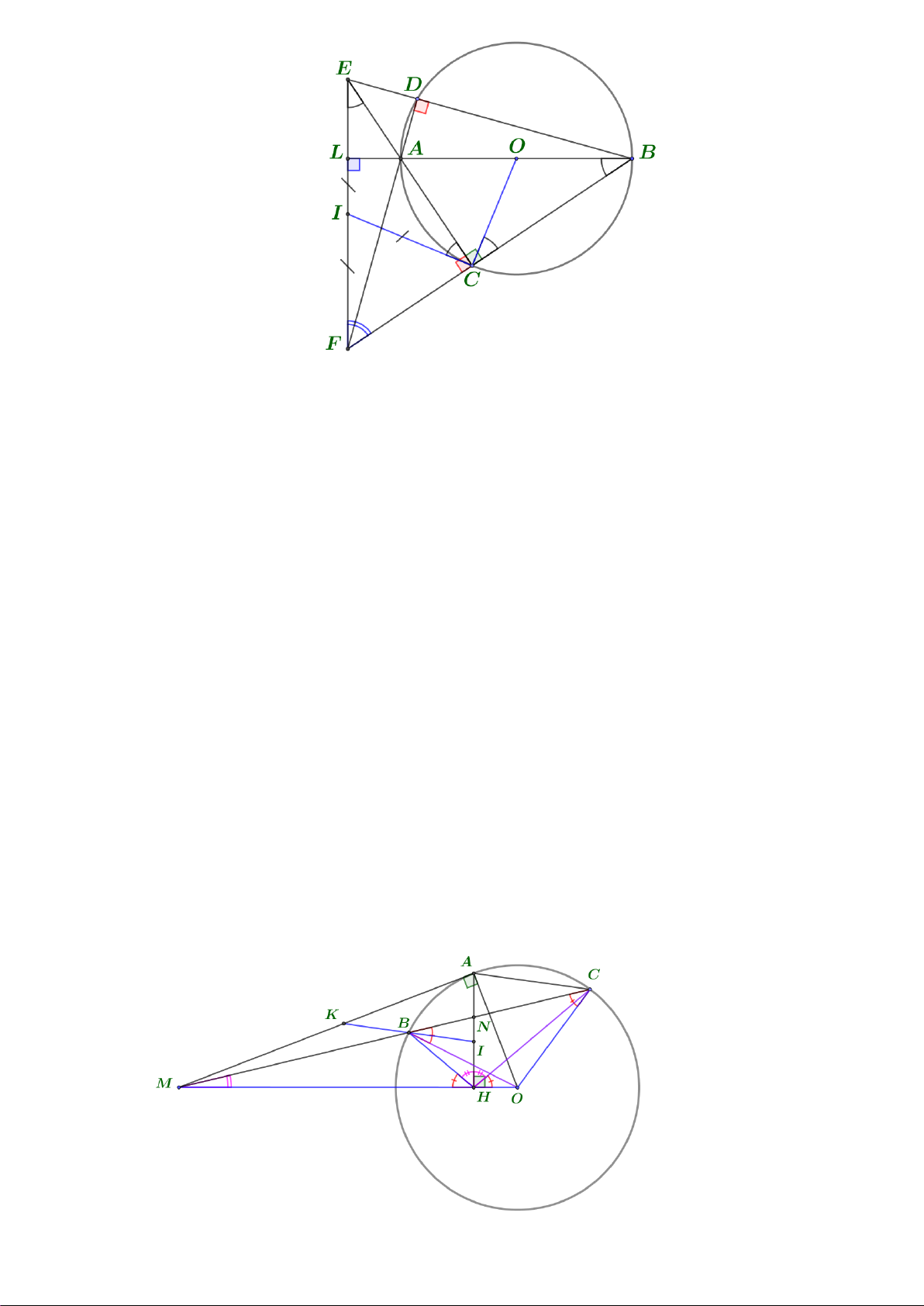
Câu 7: (1 điểm) Cho đường tròn (O) đường kính AB . Trên (O) lấy hai điểm C,D nằm khác phía
đối với AB và CD không đi qua O . Gọi E là giao điểm của AC và ,
BD F là giao điểm của AD
và BC,I là trung điểm đoạn thẳng EF . Chứng minh IC là tiếp tuyến của (O) . Lời giải ▪ Xét B EF có:
ADB ACB 90 (góc nội tiếp chắn nửa đường tròn)
BA là đường cao thứ ba. Suy ra:
BLF 90 L EF. ▪ Ta có:
CEF LBF 1 (cùng phụ với CFE ). ▪ Xét EF
C C 90 có CI là trung tuyến ứng với cạnh huyền
CI IE E
IC cân tại I . Suy ra:
CEF ICE 2 ▪ Mặt khác:
OCB LBF 3 (do O
BC cân tại O ) ▪ Từ 1 ,2,3
OCB ICE . ▪ Ta có:
OCI ICE OCAOCB OCA ACB 90 . IC OC ▪
IC là tiếp tuyến của (O).
C O
Câu 8: (2 điểm) Cho đường tròn (O) và điểm M nằm ngoài (O) , vẽ tiếp tuyến MA và cát tuyến
MBC không đi qua O(MB MC ) . Gọi H là hình chiếu vuông góc của A trên MO .
a) (1,0 điểm) Chứng minh: Tứ giác BHOC nội tiếp.
b) (1,0 điểm) Vẽ đường thẳng qua B song song với AC cắt các đường thẳng , MA AH lần lượt
tại K,I . Chứng minh KB BI . Lời giải a) ▪ Ta có: MA MB MB A MA C (g – g) 2
MA MB.MC . MC MA ▪ MA
O A 90 ,AH MO 2
MA MH.MO . ▪ Suy ra: MB MH
MB.MC MH.MO . MO MC ▪ Xét B MH và O MC có M chung và MB MH B MH O
MC c g c. MO MC ▪ Suy ra:
BHM BCO mà
BHM BHO 180 BCO BHO 180 .
▪ Vậy tứ giác BHOC nội tiếp. b) ▪ BK MB BK AC 1 AC MC ▪ BI BN BI AC 2 AC NC
▪ Do OHBC nội tiếp đường tròn nên:
OHC OBC OCB BHM . AHC OHC 90 ▪ Khi đó
AHC AHB AH là phân giác trong của BHC AHB BHM 90 HB BN HC NC ▪ Mà HB MB
HM AH HM là phân giác ngoài của BHC . HC MC ▪ Từ BK BI 1 ,2, , BK BI . AC AC
Câu 9: (1 điểm) Cho a, ,
b c là các số thực dương thỏa mãn a b c 6. Tìm giá trị nhỏ nhất của biểu thức 1 5 6 7
M (19a 22b 25c) 2 . 6 a b c Lời giải
▪ Ta có: a + b + c ≥ 6. ▪ 1 5 6 7 19 10 22 12 25 14
M (19a 22b 25c) 2
= a + + b + + c + . 6 a b c 6 a 6 b 6 c Cauchy Cauchy Cauchy ▪ Xét k, , m n 0 : 10 ka 2 10k ; 12 mb 2 12m ; 14 nc 2 14n a b c
⁎a 2 2k 5 2 10k Dấu bằng xảy ra 10 5 ka
2k 5 k . a 2
⁎ Tương tự ta tìm được: m 3 , 7 n . 2 ▪ Do đó: 5 10 12 7 14 2 2 2 M a 3b c
a b c 2 a b 2 c 3 3 3 2
M 2 25 2 36 2 49 .6 40 . 3
▪ Dấu bằng xảy ra khi a b c 2. ▪ Vậy M
40 khi a b c 2. Min ---Hết---
Document Outline
- de-tuyen-sinh-lop-10-mon-toan-chuyen-nam-2023-2024-so-gddt-tay-ninh
- HD ĐỀ CHUYÊN TOÁN (23-24)




