Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2025 – 2026 sở GD&ĐT Hà Giang

UBND TỈNH HÀ GIANG
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2025-2026
Môn: TOÁN (Đề chuyên tin) ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian giao đề Câu I. + + − − + +
(1,5 điểm) Cho biểu thức
x x 5 x 6 x 7 x 8 2x 10 x 12 A = − − x − 2 x − 3 x + 2 x +1 x − x − 6
với x ≥ 0, x ≠ 9.
1. Rút gọn biểu thức . A
2. Tìm tất cả các giá trị của x để biểu thức 4 nhận giá trị nguyên. A
Câu II. (1,0 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình 2
y = ax và đường thẳng (d ) có phương trình y = bx −1 (với a,b là các tham số). Tìm
các số hữu tỉ a,b để đường thẳng (d ) cắt parabol (P) tại hai điểm phân biệt sao cho
hoành độ một điểm là 5 3 x − = . 5 + 3
Câu III. (1,5 điểm)
1. Giải phương trình 3 2
x +1 + x − 3x −1 = 0.  2
 x +1 + y + 4 + y = 4
2. Giải hệ phương trình  . 2 2
2 xy + 4x + y + 4 − y + 4 y = 8
Câu IV. (1,0 điểm) Tìm tất cả các số tự nhiên n sao cho 2n −1 và 3n +1 là các số
chính phương và 6n −13 là số nguyên tố.
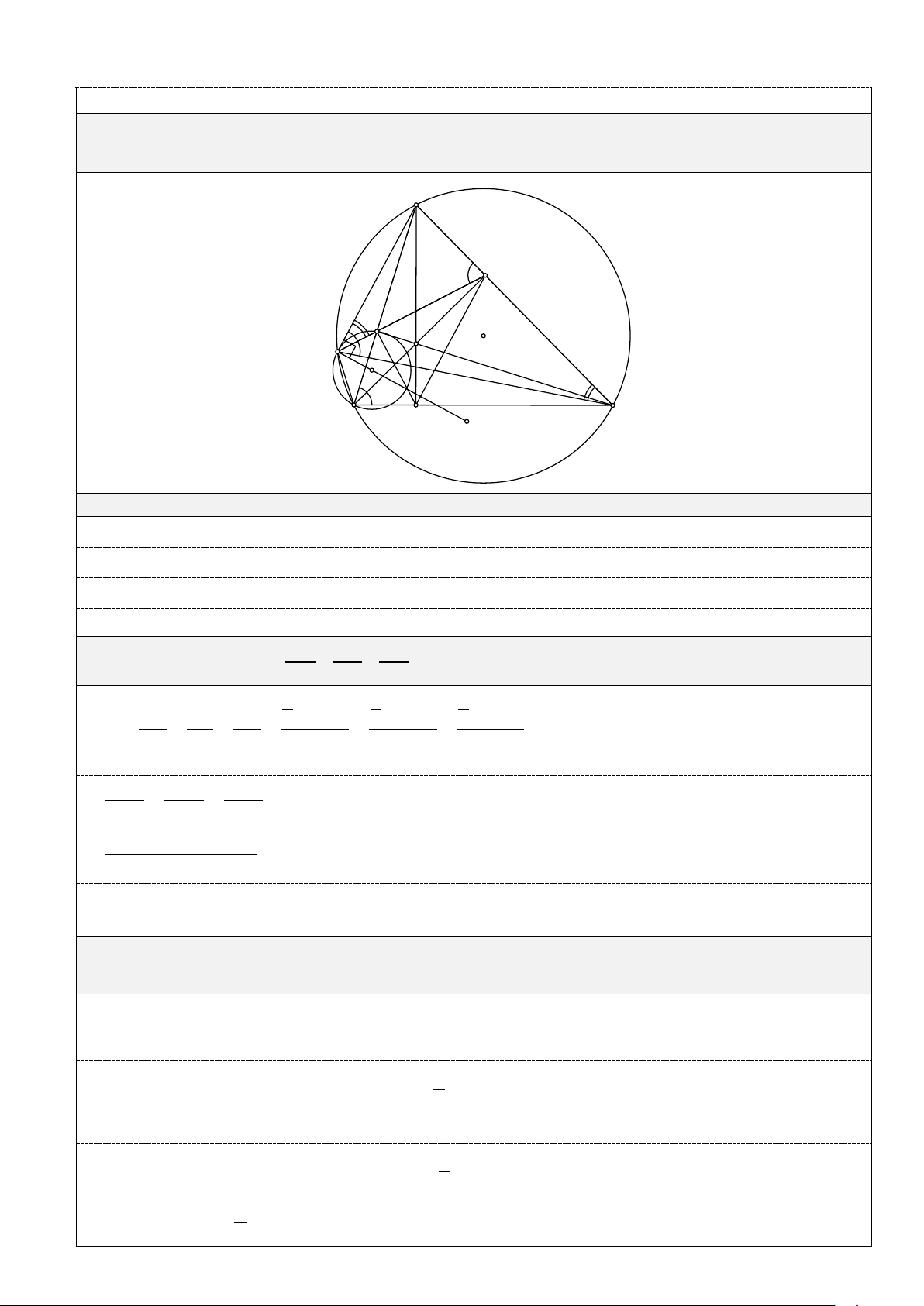
Câu V. (4,0 điểm) Cho tam giác nhọn ABC nội tiếp đường tròn (O) . Các
đường cao AD, BE, CF của tam giác ABC cắt nhau tại H.
1. Chứng minh DA là tia phân giác của góc EDF.
2. Chứng minh HD HE HF + + = 1. AD BE CF
3. Gọi M là giao điểm của tia EF với đường tròn (O) . Gọi P,Q lần lượt là tâm
đường tròn ngoại tiếp tam giác BMF và tam giác CME. Chứng minh AM ⊥ . PQ
4. Tìm mối liên hệ giữa các cạnh của tam giác ABC để biểu thức
(AB + BC + CA)2 đạt giá trị nhỏ nhất. 2 2 2
AD + BE + CF
Câu VI. (1,0 điểm) Cho a,b,c là ba số thực dương thỏa mãn điều kiện abc ≥1. Tìm
giá trị lớn nhất của biểu thức 1 1 1 P = + + . 2 2 3
a +1+ bc b +1+ ac ab(c +1) +1 --- HẾT---
Thí sinh được sử dụng máy tính bỏ túi không có chức năng soạn thảo văn bản và không có thẻ nhớ.
Họ và tên thí sinh:.................................................Số báo
danh:............................................
Cán bộ coi thi số 1..........................................Cán bộ coi thi số
2......................................... 2 UBND TỈNH HÀ GIANG
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2025-2026
HƯỚNG DẪN CHẤM MÔN TOÁN (ĐỀ CHUYÊN TIN)
(Hướng dẫn chấm gồm có 04 trang) Lưu ý:
- Thí sinh có thể làm bài theo cách khác so với đáp án nhưng đảm bảo đúng kiến thức, vẫn cho điểm tối đa.
- Không làm tròn điểm. Nội dung Điểm
Câu I (1,5 điểm) + + − − + + Cho biểu thức
x x 5 x 6 x 7 x 8 2x 10 x 12 A = − −
với x ≥ 0, x ≠ 9. x − 2 x − 3 x + 2 x +1 x − x − 6
1.(1,0 điểm) Rút gọn biểu thức . A x x x
( x + )1( x −8) 2( x +3)( x + + − + 2 ( 1)( 6) ) A = ( − − 0,25 x + ) 1 ( x −3) ( x + )2 1 ( x −3)( x +2) 2 x − x + x − ( x +3 6 8 ) = − − 0,25 x − 3 x +1 x − 3 x − 3 x x −8 = − 0,25 x − 3 x +1 x −8 = x − x + 8 = . 0,25
x +1 x +1
2.(0,5 điểm) Tìm tất cả các giá trị của x để 4 nhận giá trị nguyên. A Theo BĐT Côsi, ta có 9 A = x +1+ − 2 ≥ 2 9 − 2 = 4 0,25 x +1 Để 4 ∈ thì 9 A = 4 ⇔ x +1 =
⇔ x = 4 (thỏa mãn). Vậy x = 4. A 0,25 x +1
Câu II (1,0 điểm)
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình 2
y = ax và đường thẳng (d ) có phương
trình y = bx −1 (với a,b là các tham số). Tìm các số hữu tỉ a,b để đường thẳng (d ) cắt parabol (P) tại
hai điểm phân biệt sao cho hoành độ một điểm là 5 3 x − = . 5 + 3 2 5 3 ( 5− 3) x − = = = 4 − 15 0,25 5 + 3 ( 5 + 3)( 5 − 3)
Phương trình hoành độ giao điểm của (P) và (d ) là: 2
ax − bx +1 = 0 (*) a ≠ 0 0,25
Điều kiện để đường thẳng (d ) cắt parabol (P) tại hai điểm phân biệt:  2 b  − 4a > 0 (*) có nghiệm 2
x = 4 − 15 nên a(4− 15) −b(4− 15)+1= 0 ⇔ 15( 8
− a + b) + 31a − 4b +1= 0 0,25
Vì a,b∈Q nên ( 8
− a + b), (31a − 4b +1)∈Q 3
Nếu 8a − b ≠ 0 thì 15 31a − 4b +1 = ∈Q (vô lí) 8a − b 8  a − b = 0 a =1 Suy ra  ⇔ (thỏa mãn) 31 0,25  a 4b 1 0 b  − + =  = 8
Câu III (1,5 điểm)
1. (0,75 điểm) Giải phương trình 3 2
x +1 + x − 3x −1 = 0 Điều kiện: 3
x +1 ≥ 0 ⇔ x ≥ 1 − . 3 2
x + + x − x − = ⇔ x + ( 2
x − x + ) + ( 2 1 3 1 0 ( 1) 1 x − x + ) 1 − 2(x +1) = 0 0,25 Đặt 2 u = x +1;
v = x − x +1; u ≥ 0, 0 v >
Phương trình đã cho trở thành: 2 2
uv + v − 2u = 0 ⇔ (u − v)(2u + v) = 0 u − v = 0 u = v ⇔ ⇔  0,25 2u v 0  + = 2u = −v x = 0
Với u = v ta được 2 2
x − x +1 = x +1 ⇔ x − 2x = 0 ⇔  (thỏa mãn phương trình) x = 2 0,25
Với 2u = −v ta được 2
2 x +1 = − x − x +1 (vô nghiệm). Vậy phươ
ng trình có hai nghiệm phân biệt x = 0 và x = 2.  2
 x +1 + y + 4 + y = 4 (1)
2. (0,75 điểm) Giải hệ phương trình  2 2
2 xy + 4x + y + 4 − y + 4 y = 8 (2) x ≥ 1 − Điều kiện:  y ≥ 0 Từ (1) : 2
y − 2 = 2 − x +1 − y + 4 0,25 Từ (2) : 2 2
2 xy + 4x + y + 4 − y + 4 y = 8 ⇔
xy + x + y + − ( y − )2 2 2 2 4 4 2 = 4
Thế (1) vào (2) ta được: ⇔
xy + x + y + − ( − x + − y + )2 2 2 2 2 4 4 2 1 4 = 4 ⇔
(x + )( 2y + ) −( 2 − x + − y + + (x + )( 2y + ) 2 2 1 4 4 4 1 4 4 2 1
4 + (x +1) + (y + 4)) = 4 0,25 2 2 2
⇔ (x +1) − 4 x +1 + 4 + (y + 4) − 4 y + 4 + 4 = 0 ⇔ ( x + − ) + ( 2 1 2 y + 4 − 2)2 = 0  x +1 − 2 =  0 x = 3 ⇔  ⇔ 
(thỏa mãn). Vậy hệ phương trình có nghiệm ( ; x y) = (3;0) . 0,25 2  y + 4 − 2 = 0 y = 0
Câu III. (1,0 điểm) Tìm tất cả các số tự nhiên n sao cho 2n −1 và 3n +1 là các số chính phương và
6n −13 là số nguyên tố.
Vì 6n −13 là số nguyên tố và n ∈  nên n ≥ 3.
Ta có 2n −1 và 3n +1 là các số chính phương nên 2 2n −1 = a ; 2
3n +1 = b với ; a b∈  0,25 2 2
⇒ 2b − 3a = 5 (3) Ta có 2 2 2
6n −13 = 3(2n −1) −10 = 3a − 2(2b − 3a ) 2 2 = − = − + 9a 4b
(3a 2b)(3a 2b) (4) 0,25
Vì 6n −13 là số nguyên tố, mà 3a − 2b ≤ 3a + 2b nên từ (4) ta có 3a – 2 3 −1 b = 1 a ⇔ b = 2 2 0,25  3a −1 a = 1 − Thay 3a 1 b − = vào (3) ta được 2 2 2 −  
3a = 5 ⇔ 3a − 6a − 9 = 0 ⇔ 2  2   a = 3 a = 1 − (loại) 0,25 4
a = 3 thì b = 4,n = 5 và 6n −
13 = 17 (thỏa mãn). Vậy n = 5 là giá trị cần tìm.
Câu IV. (4 điểm) Cho tam giác nhọn ABC nội tiếp đường tròn (O) . Các đường cao AD, BE, CF
của tam giác ABC cắt nhau tại H. A E F M O H P B D C Q
1. (1,0 điểm) Chứng minh DA là tia phân giác của góc EDF.  =  0
BFH BDH = 90 ⇒  +  0
BFH BDH =180 nên BFHD là tứ giác nội tiếp ⇒  =  HDF HBF 0,25
Tương tự, CEHD là tứ giác nội tiếp ⇒  =  HDE HCE 0,25
BCEF là tứ giác nội tiếp ⇒  =  HBF HCE 0,25 Suy ra  = 
HDE HDF nên DA là tia phân giác của góc EDF. . 0,25
2. (1,0 điểm) Chứng minh HD HE HF + + = 1. AD BE CF 1 1 1 . HD BC HE.AC HF.AB Ta có: HD HE HF 2 2 2      AD BE CF 1 1 1 0,25 . AD BC BE.AC CF.AB 2 2 2 SHBC SHAC SHAB    S 0,25 ABC SABC SABC
SHBC  SHAC  SHAB  S 0,25 ABC SABC  1. S 0,25 ABC
3. (1,0 điểm) Gọi M là giao điểm của tia EF với đường tròn (O) . Gọi P,Q lần lượt là tâm đường
tròn ngoại tiếp tam giác BMF và tam giác CME. Chứng minh AM ⊥ P . Q Ta có :  = 
AEM ABC (do tứ giác BCEF nội tiếp)  0,25 = 
ABC AMC (góc nội tiếp cùng chắn 
AC của đường tròn O)⇒  =  AEM AMC ⇒ A ∆ EM 1 ∽ A
∆ MC (g g) ⇒  =  . AME ECM = 
sñME của đường tròn Q nên AM là 2 0,25
tiếp tuyến của Q ⇒ AM ⊥ QM Theo trên  1 =  AMF ACM , mà  =  ABM ACM 
= sñ MA của đường tròn O 2 0,25 1 ⇒  =  AMF FBM 
= sñ MF của đường tròn P nên AM là tiếp tuyến của P 2 5
Vì AM ⊥ PM và AM ⊥ QM nên ba điểm P,Q,M thẳng hàng. Suy ra AM ⊥ PQ . 0,25
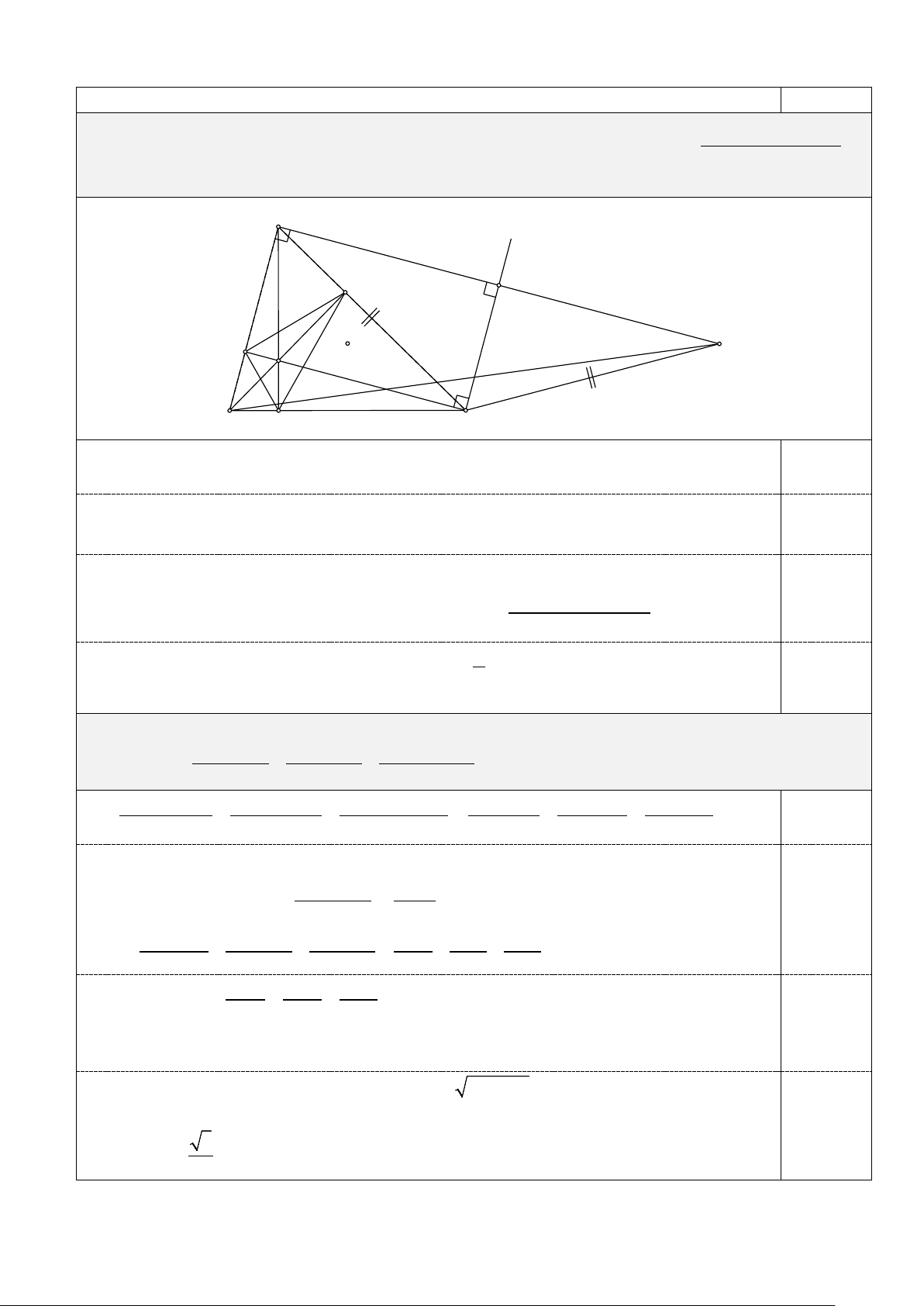
( AB + BC + CA)2
4.(1,0 điểm) Tìm mối liên hệ giữa các cạnh của tam giác ABC để biểu thức 2 2 2
AD + BE + CF
đạt giá trị nhỏ nhất. A x E N F O H B D C
Vẽ Cx  CF . Gọi N là điểm đối xứng của A qua Cx Vì  AN // 9
CF  BAN  0 ,CN  AC, AN  2CF . Ta luôn có BN  BC  CN 0,25 A
∆ BN vuông tại A nên: 2 2 2 2 2 2
AB  AN  BN  AB  4CF  (BC  CN) 0,25 2 2 2
 4CF  (BC  AC)  AB (5) Tương tự: 2 2 2
4AD  (AB  AC)  BC và 2 2 2
4BE  (AB  BC)  AC 2 + + Suy ra  2 2 2 (AB BC C ) A
AD  BE  CF  2 4
 (AB  BC  AC) hay ≥ 4 0,25 2 2 2
AD + BE + CF
Đẳng thức (5) xảy ra khi B,C, N thẳng hàng 1
AC = BN ⇒ BC = AC . 2 0,25
Vì vậy biểu thức đã cho đạt giá trị nhỏ nhất khi AB  AC  BC hay ABC là tam giác đều.
Câu V. (1,0 điểm) Cho a,b,c là ba số thực dương thỏa mãn điều kiện abc ≥1. Tìm giá trị lớn nhất của biểu thức 1 1 1 P = + + . 2 2 3
a +1+ bc b +1+ ac ab(c +1) +1 a b c a b c P = + + ≤ + + 3 3 3 3 3 3
a + a + abc b + b + abc abc(c +1) + c a + a +1 b + b +1 c + c +1 0,25
x  0 , ta luôn có 2
(x 1) (x 1)  0 3 2
 x  x  x 1 0 3 2
 x  x 1 x  2x x 1  
, đẳng thức xảy ra khi x 1. 3
x  x 1 x  2 0,25 Suy ra a b c 1 1 1 + + ≤ + + 3 3 3
a + a +1 b + b +1 c + c +1 a + 2 b + 2 c + 2 Ta sẽ chứng minh 1 1 1 + + ≤ 1 (6)
a + 2 b + 2 c + 2
Thật vậy, (6)  (a  2)(b  2)  (b  2)(c  2)  (a  2)(c  2)  (a  2)(b  2)(c  2) 0,25
 ab  bc  ca  abc  4
Áp dụng bất đẳng thức Côsi ta có 3
ab + bc + ac ≥ 3 . ab . bc ca = 3
Mặt khác abc ≥1  ab  bc  ca  abc  4 nên (6) đúng, suy ra P ≤ 1. 0,25 Vậy 3 max P =
khi a = b = c = 1. 3 ---HẾT---
Xem thêm: ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN
https://thcs.toanmath.com/de-thi-tuyen-sinh-lop-10-mon-toan
Document Outline

• 017_Tuyển sinh 10_Toán Chuyên_mới_tỉnh_Hà Giang_25-26
• TUYEN SINH 10