

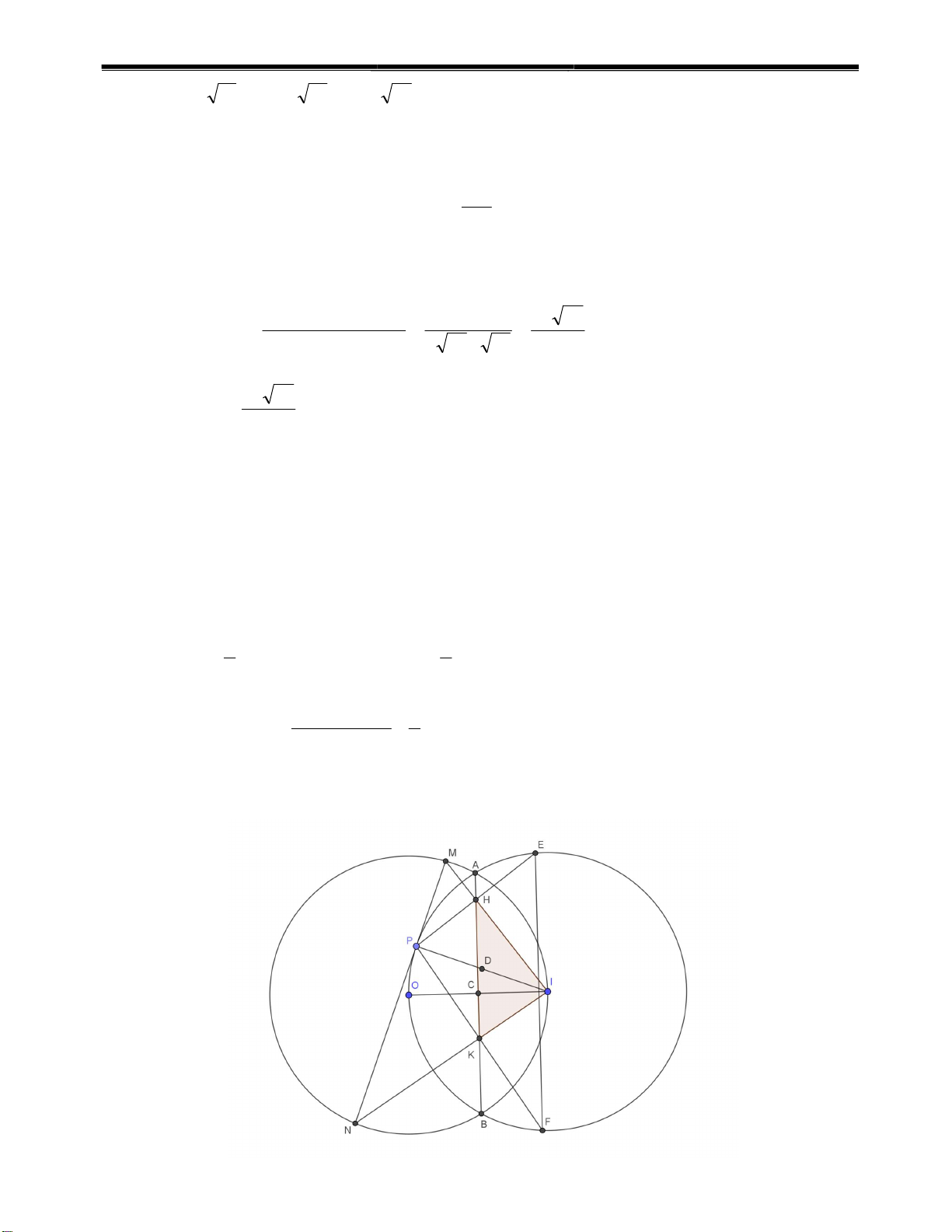

Preview text:
CLB Toán Cơ Sở Phòng Nội Dung
HƯỚNG DẪN GIẢI ĐỀ THI CHUYÊN TOÁN TỈNH HƯNG YÊN 2025 Câu I. x 4 0 x 4
a. Điều kiện xác định: x x 2x 4 x 8 0 (
x 4)( x 2) 0 x , 0 x 4. x , 0 x 0 x 0 Ta có: 1 3 x 10 x 4 x 4 M 2
x 4 x x 2x 4 x 8 4 x x 2 3 x 10 x 4 x 4
(x 4)( x 2) (x 4)( x 2) 4 x 4 x 8 ( x 2)2 1 . . ( x 2)2 ( x 2) 4 x x 1 Vậy M , x , 4 x 0. x 9x 2 x 4 4 2 2 b. Ta có: N M 9 .( x 2 x ) 4 9 x 2 34 x 10 . 10 4 x x x Như vậy min N 1 .
0 Dấu bằng xảy ra khi và chỉ khi 2 2 4 34 x x x . 4 x 3 9 Câu II.
a. Giả sử (d) cắt (P) tại hai điểm phân biệt. Khi đó phương trình hoành độ x2 2 x m có hai nghiệm phân biệt x , x . 1 2 Ta có: 2 2
x x m 0 có hai nghiệm phân biệt x , x khi 1 8m . 0 1 2 Khi đó: 2 2 x x m 0 2 2
x x m x x . Tương tự 2 2 x x m x x . 1 1 1 2 1 2 2 1 2 1 1 m
Theo định lý Viet thì x x , x x . 1 2 2 1 2 2 Như vậy 4 (2 2 x x m)2 (2 2
x x m)2 (x x )2 (x x )2 (x x )2 2. 1 2 2 1 1 2 2 1 1 2 2 1 7
Hay là: 2 (x x ) 4x x 2m m . Thử lại ta thấy thoả mãn. 1 2 1 2 4 8 2 CLB Toán Cơ Sở Phòng Nội Dung 7
Vậy m là giá trị cần tìm thoả mãn yêu cầu bài toán. 8 b. Điều kiện: 2 x y . 0 Ta có: Đặt 2
a x y 0 . Từ (1) khi đó 3 x x( 2 x y ) 2 ( 2 x y )3 0 3 2 x ax 2 3 a 0 (x a)( 2 x 2ax 2 2 a ) 0. Mà 2 x 2ax 2 2 a (x a)2 2 a . 0 Suy ra 2
x a x x y , x . 0 (*)
Ta bình phương hai vế (*) lên ta có: 2 2
y x x . Thay vào (2) thì 56 2 x 2 ( 0 2 2 x x x ) 4x 8 ( x ) 1 2 96 2 3 x 20x 2 3 4x 8 ( x ) 1 . Ta có: 63 4x 8 ( x ) 1 33 . 2 16x 8 .( x ) 1 24x . 3 Và 6 9 .( 6 2 x 20x ) 2 5 ( 76 2 x 144x ) 9 24x 3 (24x )
3 2 24x 3 24x 3. Như vậy 2 3 96x 20x 2 4x 8 ( x )
1 , đẳng thức xảy ra khi và chỉ khi 1
2 16x 8x 1 x . (tm) 8 1 7 1 7 2 2 7 7 Suy ra y x x y . Thử lại các cặp , , , đều thoả mãn. 64 8 8 8 8 8 1 7 1 7
Vậy hệ phương trình có các nghiệm là: , , , . 8 8 8 8 Câu III.
1. Giả sử phương trình ( 2 x ) 3 2
y (x 2y)(x 2 y )
1 25x 2y 169(*) có nghiệm nguyên. Ta có
phương trình (*) tương đương 2 2 x y 7 2 2
y x x 2y 25x 2y 169 ( 2 x 7) 2 2
y x 26x 169 (x ) 13 2. Như vậy 2
x 7 là số chính phương. Đặt x2 7 z2, z là số nguyên dương.
Khi đó 7 (z x)(z x). Do z x z x 2z 0. Ta xét hai trường hợp: 3 CLB Toán Cơ Sở Phòng Nội Dung z x 1 x 3 Trường hợp 1: . Suy ra 2 y 16 y 4 . z x 7 z 4 z x 7 x 3 2 25 5 Trường hợp 2: . Suy ra y y . (loại) z x 1 z 4 4 2
Như vậy phương trình (*) có các nghiệm (x, y) thoả mãn là , 3 ( 4), , 3 ( 4 ).
2. Gọi số quả bóng có màu đỏ, màu xanh trong thùng lần lượt là: x, . y
Số cách lấy ngẫu nhiên một quả bóng từ trong thùng là 40 (cách).
Số cách để lấy được một quả bóng màu đỏ là: x (cách). 3 x 3
Vì xác suất để lấy được quả bóng màu đỏ là . Như vậy x 12. 10 40 10
Số cách để lấy được một quả bóng màu xanh là: y (cách). 3 y 3
Vì xác suất để lấy được quả bóng màu xanh là . Như vậy x 15. 8 40 8
Do đó số quả bóng có màu khác trong thùng là 40 - 12 - 15 = 13.
Vậy số quả bóng có màu khác xanh và đỏ là 13 (quả). Câu IV.
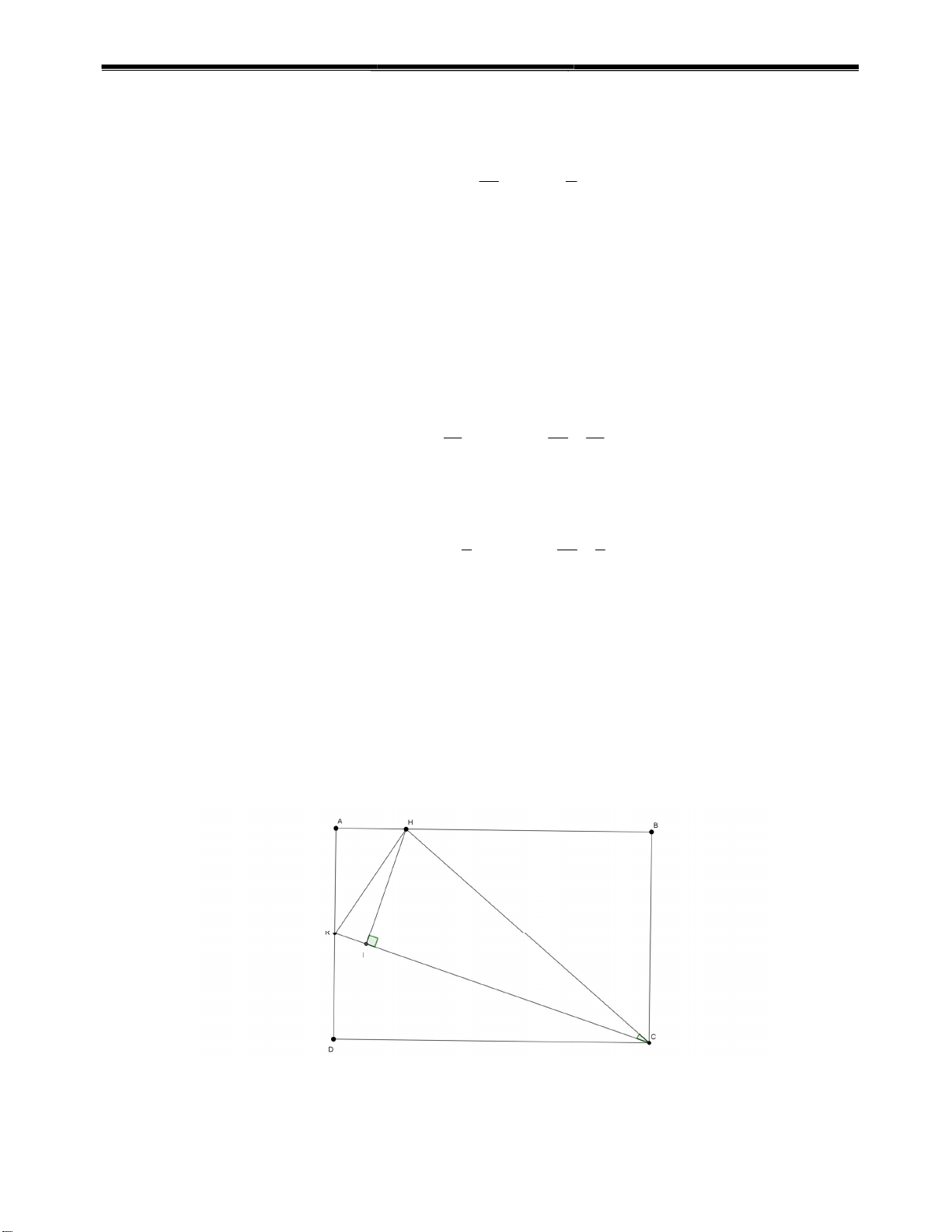
Kẻ đường cao HI của tam giác HKC. Do K là trung điểm AD nên AK = KD = 3 (cm). Ta có:
BH AB AH 9 2 7(cm).
Áp dụng định lý Pitago cho các tam giác vuông KAH, BHC, KDC thì 2 2 2 KH AH AK , 13 2 2 2 KC KD DC , 90 2 2 2 HC HB BC 85. 4 CLB Toán Cơ Sở Phòng Nội Dung
Suy ra KH 13, KC 3 10, HC 85(cm). Ta có: 2 2 2 2 2
KH HI KI HC IC (KC IC)2 2 2 HC KC 2KC.IC. IC
Mà tam giác HIC vuông tại I nên cos H CK IC HC.cos HCK. HC Như vậy 2 2 2
KH HC KC 2KC.HC.cos H CK. 2 2 2 HC KC KH 85 90 13 27 34 Do đó: cos HCK . 2KC.HC 2 85 3 . 10 170 27 34 Vậy cosHCK . 170 Câu V.
1) Gọi C là giao điểm của OI và HK, và D là trung điểm của IP.
Do tam giác IPK vuông tại K và tam giác IPH vuông tại H nên DK = DP = DI = DH.
Như vậy bốn điểm P, K, I, H thuộc cùng một đường tròn. 1 1 Ta có: I KH I DH HPI PM I NOI. 2 2 180 NOI 1 Suy ra CIH IKH NOI 90 . 2 2
Vậy HK vuông góc OI tại C. 5 CLB Toán Cơ Sở Phòng Nội Dung
2) Ta gọi giao của PH, PK với (I,R) lần lượt là E, F.
Do tam giác IPE cân tại I có IH vuông góc EP nên H là trung điểm PE.
Giả sử AH cắt (O,R) tại B’ thì H . A HB' HM. 2 HI HP H . P H . E
Như vậy tứ giác APB’E nội tiếp. Hay B’ thuộc (I,R) nên B’ trùng B.
Do đó H thuộc AB, tương tự thì K cũng thuộc AB.
Như vậy A,H,K,B thẳng hàng.
Ta có AO = AI, BO = BI nên AB là đường trung trực của OI nên C là trung điểm OI. 1 1 2 R R Ta có: S IC.HK . . IO HK .IP
(do IP là đường kính của đường tròn (D, DI)) HIK 2 4 4 4 1
Dấu bằng xảy ra khi và chi khi R IP HK EF. Tức là EF là đường kính của (I,R). Hay P 2 trùng với O. 2 R Vậy GTLN của S là khi P trùng với O. HIK 4 Câu VI. C S Ta có: ( 5 2 2 x 2 2
xy y ) 22 12 (x y)2 2
x 2(x y) x2 (3x 2y)2. x y 2 2 x 2 2 xy y x y x 2 2 3 ( 2 )2 Suy ra 3 2 1 2 (x y) x hay 1 . 5 x 2 y 5(x 2 y) 5 x 2 y
Chứng minh tương tự ta cũng có: 2 2 y 2 2 yz z 1 2y 2 2 z 2 2 zx x 1 2z 1 , 1 . y 2z 5 y 2 z z 2x 5 z 2x
Khi đó ta cộng vế theo vế và áp dụng bất đẳng thức cộng mẫu thì 3 2 x y z 3 2 2 2 2 x y z P 5
5 x 2y y 2z z 2 x 5 5 2 x 2 2 xy y 2 2 yz z 2 zx 3 2 (x y z)2 3 2 . 5. 5 5 2 2 2
x y z 2xy 2 yz 2zx 5 5
Vậy min P 5. Dấu bằng xảy ra khi và chi khi x = y = z. 6
Document Outline
- de-tuyen-sinh-lop-10-mon-toan-chuyen-nam-2025-2026-so-gddt-hung-yen
- Hưng Yên. De thi Chuyen Toán Hưng Yên 2025




