Đề tuyển sinh lớp 10 môn Toán (chuyên) năm 2025 – 2026 sở GD&ĐT Phú Yên

CLB Toán Cơ Sở Phòng Nội Dung
HƯỚNG DẪN GIẢI ĐỀ THI CHUYÊN TOÁN TỈNH PHÚ YÊN Năm học 2025 – 2026 Câu 1 a) Với x  , 0 x  1,ta có
x 1 x x 1 x2  x x  x 1
x 1 x  x 1 x2  x x 1 P       x x  x x  x x x x x  x x (2x  2  x 1
)(  x)  x2  x x  x 1  x2  2x x  2 x 1 P   x 1 (  x) x 1 (  x)  ( x  )( 1 x  ) 1 3 x  2 x 1 P   x 1 (  x) x 9 9 x 9 9 9 Khi đó 0     . Do để nguyên. P x  2 x 1 1 4 x   2 P x  7  3 5  47  21 5  x  x 
TH1: 9  1 P  9   2   2 (thỏa mãn) P  7  3 5  47  21 5  x  x   2  2  x  2 x  4 9 9 TH2:    2  P    (thỏa mãn) P 2  1 1 x  x   2  4 47  21 5 47  21 5 1 
Vậy tập các giá trị của x thỏa mãn là  ; ; ; 4 .  2 2 4 b) Ta có 2 2 6 1 b 3  b 6  2  0 
  3  0  là nghiệm của phương trình 2 2 x  6x  3  0 b2 b b
Mà a cũng là nghiệm của phương trình 2 2
x  6x  3  0 , nên theo Vi-ét ta có:
1 a  3 ab1 3b b     3b . a 3 a     2 b 2 6075 3 b 6075 3 b Thay vào P ta được: P    2025 20 2 ab  (ab  ) 1 3 3b . 20 . 2 b  (3b)3 2 Vậy P  2025 . Câu 2. 2 a) ĐKXĐ 3x  ,
2 x 1  0  x   . Đặt a  3x  2,b  x  , 1 a,b  . 0 Suy ra 2 x  a  2 2 b . 3 2 CLB Toán Cơ Sở Phòng Nội Dung Ta có: x  3 2
x  5x  2  3x  2  2 x 1 2  a  2 2 b  ab  a  2 . b Suy ra (a  2 )( b a  ) b  a  2 . b
Trường hợp 1: a  2b  0  a  b  0  3x  2  x 1  . 0 (vô nghiệm)
Trường hợp 2: a  b 1  3x  2  x 1  .
1 Ta bình phương hai vế của phương trình thì
3x  2  x  2  2 x 1  x  x  . 1  2 1 5 Với x  .
0 Ta có: x  x 1  x  . 2 1 5 Thử lại thấy x 
thoả mãn phương trình ban đầu. 2 1   5 
Vậy tập nghiệm của phương trình là  .  2  
b) Gọi x , x là hai nghiệm nguyên của phương trình P(x)  . 0 Giả sử x  x 1 2 1 2
Suy ra P(x)  (x  x )(x  x ). Theo định lý Vi - ét, ta có: x x  c  . 4 (1) 1 2 1 2 Mà P( )
4  4  x 4  x là số nguyên tố. 1 2 x  5 TH1: Nếu 4  x 1 1  . 1 x  3  1 4
+ Với x  3. Như vậy x   x , vô lý. 1 2 3 1 4
+ Với x  5 . Như vậy x   x  0  x , vô lý. 1 2 5 2 1 x  5 TH2: Nếu 4  x 1 2  . 2 x  3  2
+ Với x  3. Như vậy x  1 x  0. 2 1 1
Khả năng 1: x  0 thì P( )
4  4 không là số nguyên tố. 1
Khả năng 2: x 1 thì b  (  x  x )   , 4 c  x x  . 3 1 1 2 1 2 4
+ Với x  5 . Như vậy x   x  . 0 Khi đó P( ) 4  4 2 1 5 1
không là số nguyên tố. Vậy b   , 4 c  , 3 P(x) 2  x  4x  . 3 Câu 3. 3 CLB Toán Cơ Sở Phòng Nội Dung
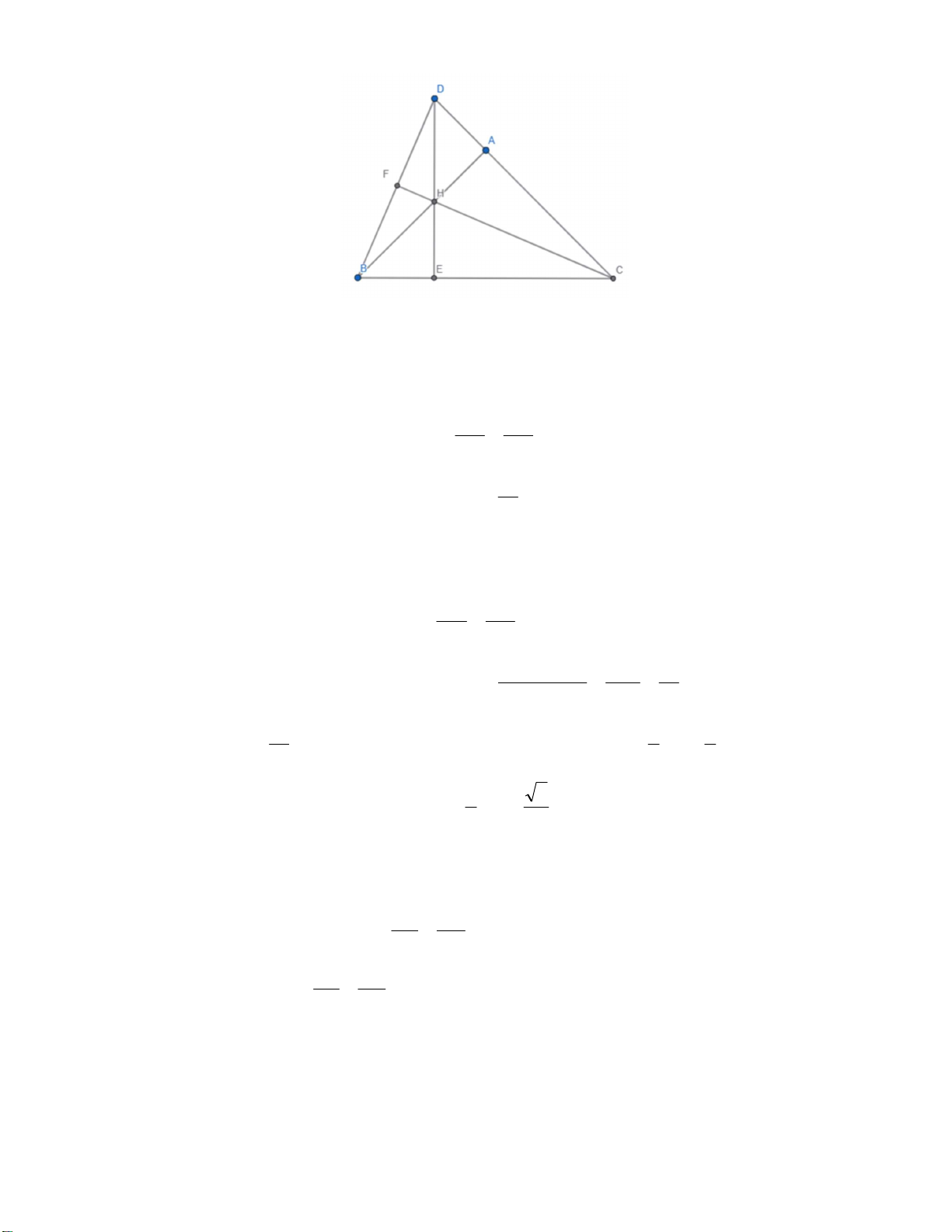
a. Do BA vuông góc AC và DE vuông góc BC nên H là trực tâm của tam HBC. Suy ra HC vuông BD tại F. Ta có 
DFH  HEC  90 và FH  D  EH  C suy ra FH HD FH  D ~ EH  C(g.g)    FH.HC  H . E H . D EH HC 2 a b. Theo định lý Pitago 2 2 2 2 BC  AB  AC  AB  . 2 Ta có: ADH  45 .
 Suy ra tam giác ADH vuông cân tại A và AD = AH.
Bằng cách chứng minh tương tự câu a thì FH HB F  HB ~ AH  C    FH.HC  H . A H . B AH HC (HA  HB)2 2 2 AB a
Theo bất đẳng thức AM - GM: FH.HC  H . A HB    . 4 4 8 2 a 1 1 Vậy max(FH.HC) 
. Dấu bằng xảy ra khi và chỉ DA  AH  BH  AB  A . C 8 2 2 1 2
Như vậy khi D thuộc tia đối AC sao cho DA  AC  . a 2 4 Câu 4.
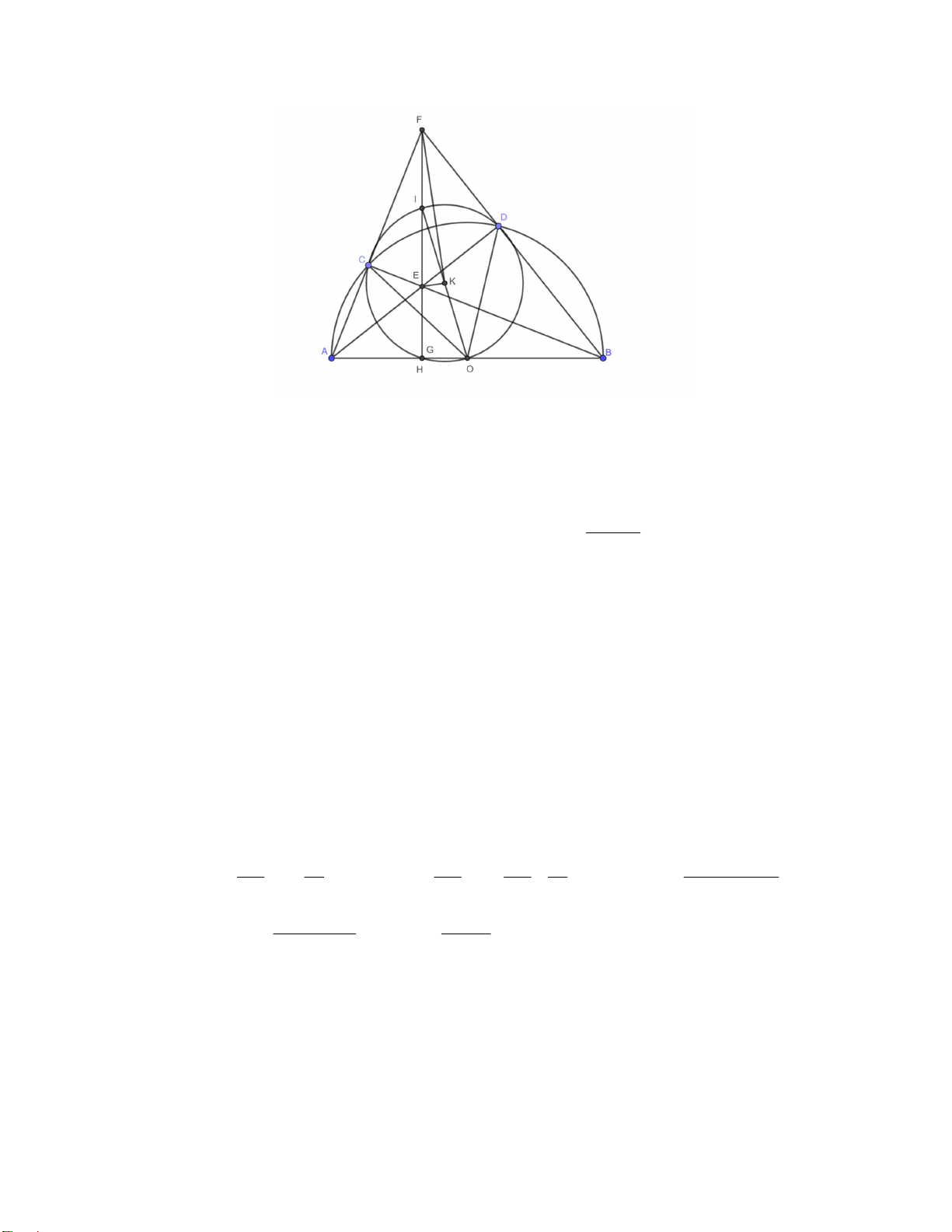
a. Gọi hình chiếu của E lên BC là G. AE AG Khi đó, ta có A  GE ~ A  D ( B g.g)    A . E AD  A . B AG ) 1 .( AB AD BE BG Và B  GE ~ B  C ( A g.g)    B . E BC  B . A B .( G ) 2 BA BC Từ (1) và (2) ta có: . AE AD  . BE BC  ( BA AG  G ) 2 B  BA  4 2 a .
b. Ta thấy ADB  ACB  90 suy ra E là trực tâm của tam giác FAB. Hay EF vuông góc AB.
Gọi I’ là trung điểm của EF. Khi đó ta có I’E = I’F = I’C= I’D.
Ta có: I' DO 180  I' DF  ODB 180  I' FB  ABF  90 . 4 CLB Toán Cơ Sở Phòng Nội Dung Tương tự: I'CO 90 . 
Như vậy I’ thuộc đường tròn ngoại tiếp tam giác COD.
Khi đó I trùng I’. Từ đó cũng suy ra H thuộc đường tròn đường kính IO. Suy ra IHO 90 . 
Do đó H trùng G và F, I, H, E thẳng hàng. COD
c. Ta có: CKD  2COD  120 ,CFD  90  CBF  90   60 . 2
Suy ra CKD  CFD 180 . 
Khi đó tứ giác F, D, K, C nội tiếp.
Kết hợp KC = KD, do đó AK là phân giác góc AFB.
Lưu ý: Các kiến thức về góc ở tâm, tứ giác nội tiếp học sinh tự chứng minh.
Câu 5. Giả sử a, b, c, d là các số nguyên thoả mãn 3 a  64 3 b  2024 3 c  2026 3 d  . 0 (*) Ta có 3 a  a  (a  ) 1 a(a  ) 1 3 khi đó 3 a  a(mod ) 3 , 3 b  ( b mod ) 3 , 3 c  c(mod ) 3 , 3 d  d(mod ) 3 .
Ta lấy mod 3 hai vế của (*) thì a  b  c  d  ( 0 mod ) 3 .
Suy ra (a  b  c  d)2  ( 0 mod ) 9 .
Câu 6. Sử dụng khi triển Abel ta có: 169    2 81 2 2 2 169 2 169 81 2 2 169 2 2 x 81 2 y 250  .y  .x  ( y  x ).  x   y  x  x . 2 2 2  2 2  2 2 y x y  y x  x y x  y xy 2 13 ( 9 )2 2 2 (2 )2 2 2 2  y  x   y  x   x  y . 2 2 y 2 2 y Do 13  y  x  , 0 2xy  13x  9 . y Vậy 250 2 2
 x  y . Dấu bằng xảy ra khi và chỉ khi y 1 , 3 x  . 9 5
Document Outline

• Doc1
• Phu Yen. Chuyen Toan 2025