Đề tuyển sinh lớp 10 môn Toán (chuyên Toán) năm 2022 – 2023 sở GD&ĐT Tiền Giang

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi chính thức kỳ thi tuyển sinh vào lớp 10 Trung học Phổ thông môn Toán (chuyên Toán) năm học 2022 – 2023 sở Giáo dục và Đào tạo tỉnh Tiền Giang; kỳ thi được diễn ra vào ngày 18 tháng 06 năm 2022. Mời bạn đọc đón xem!

39 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

6 trang 8 tháng trước

Tác giả:

Profile Vũ Hường
--------------------------------------------------------------------------------------------------------------------
Bài 1. (3,0 điểm)
1) Rút gọn các biểu thức:
111 1 1
1 2 2 3 3 4 14 15 15 16
M
=++++ +
+++ + +
;
( )
( )
3
2 3 1 6 3 10
10 2 3 5
N
−+
=
−+
.
2) Giải phương trình
(
)
(
)
22
13919131
xx x x+ + +− =
.
3) Giải hệ phương trình
2
32
2 14
3
x xy x
x xy y x
+ +=
+ +=
.
Bài 2. (3,0 điểm)
1) Trong mặt phẳng tọa độ
Oxy
, cho parabol
( )
2
:P y ax=
qua
( )
3;3M
và đường thẳng
( )
1
:
2
d y xm=−+
(với
là tham số). Xác định phương trình của parabol
( )
P
, từ đó
tìm tất cả các giá trị của tham số
m
để đường thẳng
( )
d
cắt parabol
( )
P
tại hai điểm
phân biệt
( ) ( )
;, ;
AA BB
Axy Bxy
khác gốc tọa độ, sao cho
25
16
AB
BA
yy
xx
+=
.
2) Gọi
12
,xx
là hai nghiệm của phương trình
2
10x mx+ +=
và
34
,xx
là hai nghiệm của
phương trình
2
10x nx+ +=
, với
,mn
là các tham số thỏa mãn
2m ≥
,
2
n
≥
.
Chứng minh rằng:
( )( )( )( )
22
13231424
xxxxxxxx nm− − + +=−
.
3) Cho hai số
,xy
liên hệ với nhau bởi đẳng thức
( )
22
2 2 10 21 0x y xy x y+ − + −+=
.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2S xy=−+
.
Bài 3. (1,0 điểm)
Tìm tất cả các cặp số nguyên
( )
;xy
thỏa mãn
2
21
1
x
y
xx
−
=
−+
.
Bài 4. (3,0 điểm)
Cho tam giác nhọn
( )
ABC AB AC<
nội tiếp đường tròn tâm
O
, có ba đường cao
,,AD BE CF
(
)
,,D BC E AC F AB∈∈∈
cắt nhau tại
.
H
Tia
AO
cắt
BC
tại
M
và cắt
( )
O
tại
N
; gọi
,PQ
lần lượt là hình chiếu của
M
trên
,.AB AC
Chứng minh:
1)
DH
là tia phân giác của
EDF
.
2)
HE NB
HF NC
=
.
3)
.. ..HE MQ HB HF MP NC=
.
----------------------------------------------------- HẾT ------------------------------------------------------
Thí sinh được sử dụng các loại máy tính cầm tay do Bộ Giáo dục và Đào tạo cho phép.
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không được giải thích gì thêm.
Họ và tên thí sinh: ..................................................... Số báo danh: ...................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH TIỀN GIANG
ĐỀ THI CHÍNH THỨC
(Đề thi có 01 trang, gồm 04 bài)
KỲ THI TUYỂN SINH LỚP 10
TRUNG HỌC PHỔ THÔNG NĂM HỌC 2022-2023
Môn thi: TOÁN (CHUYÊN TOÁN)
Thời gian làm bài: 150 phút
(Không kể thời gian phát đề)
Ngày thi: 18/6/2022.
Trang 1/5
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH TIỀN GIANG
ĐÁP ÁN ĐỀ THI CHÍNH THỨC
(Đáp án có 05 trang)
KỲ THI TUYỂN SINH LỚP 10
TRUNG HỌC PHỔ THÔNG NĂM HỌC 2022-2023
Môn thi: TOÁN (CHUYÊN TOÁN)
---------------------------------------------------------------------------------------------------------------------
I. Hướng dẫn chấm thi:
- Cán bộ chấm thi chấm 2 vòng độc lập.
- Cán bộ chấm thi không tự ý thay đổi thang điểm trong đáp án.
- Mọi cách giải khác, nếu đúng vẫn ghi đủ điểm.
II. Đáp án và thang điểm:
Bài
Nội dung
Điểm
1
(3,0đ)
1) Rút gọn các biểu thức: 1,0
111 1 1
1 2 2 3 3 4 14 15 15 16
M =++++ +
+++ + +
;
2 1 3 2 4 3 15 14 16 15M =−+−+−++−+−
0,25
16 1 3M = −=
0,25
( )
( )
( )
(
)
( )
3
3
3
2 31 31
2 3 1 6 3 10
10 2 3 5 5 1 6 2 5
N
−+
−+
= =
− + −+
0,25
( )( )
( )( )
2 31 31
4
1
4
51 51
N
−+
= = =
−+
0,25
2) Giải phương trình
(
)
(
)
22
13919131xx x x+ + +− =
1,0
2
2
13 9 1
1
9 13
xx
xx
++
=
++
22
1391913xx x x⇔+ += ++
0,25
( )
(
)
2
3 1 9 11 0xx
⇔ − +− =
0,25
3 10x⇔ −=
hoặc
2
9 11 0x
+−=
0,25
1
3
x⇔=
hoặc
0x =
. Vậy
1
0;
3
S

=


0,25
Cách khác:
(
)
(
)
(
)
(
)
22 2 2
1391913 913 913xx xxxxxx+ + +− = +− ++
0,25
Trang 2/5
22
1391913xx x x⇔ + += ++
2
9 13 0xx⇔ +− =
(vô nghiệm) hoặc
(
)
(
)
2
3 1 9 11 0xx− +− =
0,25
3 10x⇔ −=
hoặc
2
9 11 0x +−=
0,25
1
3
x⇔=
hoặc
0x =
Vây
1
0;
3
S

=


0,25
3) Giải hệ phương trình
2
32
2 14
3
x xy x
x xy y x
+ +=
+ +=
1,0
Ta có
( )
0; y
không là nghiệm của hệ nên hệ phương trình đã cho được viết lại:
2
1
24
3
xy
x
y
x xy
x
++ =
+ +=
0,25
( )
( )
1
4
1
4
xy x
x
xyx
x

+++ =


⇔

+ +=


0,25
2
1
2
xy
x
x
+=
⇔
+=
0,25
1
1
x
y
=
⇔
=
. Vậy hệ có tập nghiệm
(
)
{
}
1;1S =
.
0,25
2
(3,0đ)
1) Trong mặt phẳng tọa độ
Oxy
, cho parabol
( )
2
:P y ax=
qua
( )
3;3M
và
đường thẳng
(
)
1
:
2
d y xm=−+
(với
m
là tham số). Xác định phương trình của
parabol
( )
P
, từ đó tìm tất cả các giá trị của tham số
để đường thẳng
( )
d
cắt
parabol
( )
P
tại hai điểm phân biệt
( ) ( )
;, ;
AA BB
Axy Bxy
khác gốc tọa độ, sao cho
25
16
AB
BA
yy
xx
+=
.
1,25
( )
( )
( )
2
2
3;3 : 3 3 1
M P y ax a a∈ = ⇔= ⇔=
0,25
Vậy parabol
( )
2
:
Pyx=
0,25
Trang 3/5
Phương trình hoành độ giao điểm của
( )
P
và
( )
d
:
2
1
2
x xm=−+
2
2 20xxm⇔ +− =
có
1 16m∆= +
Để đường thẳng
( )
d
cắt parabol
(
)
P
tại hai điểm phân biệt
( ) ( )
;, ;
AA BB
Axy Bxy
khác gốc tọa độ
1
16
m⇔ >−
và
0
m ≠
.
0,25
Theo định lý Vi-et, ta có:
1
, .
2
A B AB
x x xx m
+=− =−
2 2 33
25 25 25
16 16 . 16
ABABAB
B A B A AB
y y x x xx
x x x x xx
+
+=⇔+=⇔ =
0,25
( ) ( )
( )
3
3
11
3
3.
25 25
22
. 16 16
AB ABAB
AB
m
xx xxxx
xx m
 
− −− −
 
+− +
 
⇔ =⇔=
−
13
25
82
2 24 25
16
m
mm
m
−−
⇔ = ⇔− − =−
−
2m
⇔=
(thỏa điều kiện).
0,25
2) Gọi
12
,xx
là hai nghiệm của phương trình
2
10
x mx+ +=
và
34
,xx
là hai
nghiệm của phương trình
2
10
x nx+ +=
, với
,
mn
là các tham số thỏa mãn
2m ≥
,
2n ≥
. Chứng minh rằng :
( )( )( )(
)
22
13231424
.xxxxxxxx nm− − + +=−
0,75
Theo định lý Vi-et, ta có :
12
12
1
xx m
xx
+=−
=
và
34
34
1
xx n
xx
+=−
=
0,25
Ta có:
(
)(
)(
)(
)
13231424
VT
xxxxxxxx=−−+ +
( ) (
)
22
12 3 1 2 3 12 4 1 2 4
xx x x x x xx x x x x

= − ++ + ++

0,25
( )
( )
22
33 44
11mx x mx x
=++ −+
(
)( )
33 44
mx nx mx nx= − −−
0,25
( ) ( )
34
n mx m nx=−+
22
n m VP=−=
.
3) Cho hai số thực
,xy
liên hệ với nhau bởi đẳng thức
( )
22
2 2 10 21 0x y xy x y+ − + −+=
. Tìm giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
2
S xy=−+
.
1,0
Viết lại biểu thức đã cho thành
( ) ( )
2
2
2 6 25xy xy y−+ + −+ +=−
.
0,25
Như vậy với mọi
x
và mọi
y
ta luôn có
2
6 50SS+ +≤
(với
2S xy=−+
)
0,25
Suy ra:
( )( )
5 10 5 1SS S+ + ≤ ⇔− ≤ ≤−
. Do đó:
0,25
Giá trị nhỏ nhất của
S
bằng
5−
khi
7
0
x
y
= −
=
Giá trị lớn nhất của
S
bằng
1−
khi
3
0
x
y
= −
=
.
0,25
Trang 4/5
3
(1,0đ)
Tìm tất cả các cặp số nguyên
( )
;xy
thỏa mãn
2
21
1
x
y
xx
−
=
−+
.
1,0
Ta có:
2
21
1
x
y
xx
−
=
−+
( )
2
2 10yx y x y⇔ − + + +=
.
0,25
1
0
2
yx
=⇒=
(không thỏa).
0y ≠
, phương trình có nghiệm khi và chỉ khi
( )
( )
2
22
2 4 10
33
y yy y
∆= + − + ≥ ⇔− ≤ ≤
.
0,25
Vì
y ∈
và
0y ≠
nên
{ }
1;1y ∈−
.
2
1 3 20 1y xx x=⇒ − +=⇔=
hoặc
2x =
.
0,25
2
1 01y xx x=−⇒ + = ⇔ =−
hoặc
0x =
.
Vậy có 4 cặp số cần tìm là
(
) ( ) ( ) ( )
1;1,2;1, 1; 1,0; 1−− −
.
0,25
4
(3,0đ)
Cho tam giác nhọn
( )
ABC AB AC<
nội tiếp đường tròn tâm
,O
có ba đường cao
,,AD BE CF
(
)
,,
D BC E AC F AB
∈∈∈
cắt nhau tại
.H
Tia
AO
cắt
BC
tại
M
và cắt
( )
O
tại
,N
gọi
,PQ
lần lượt là hình chiếu của
M
trên
,.AB AC
3,0
1) Chứng minh:
DH
là tia phân giác của
EDF
.
1,0
Hình vẽ
0,25
Chứng minh đúng hai tứ giác
,BFHD CEHD
nội tiếp.
0,25
Suy ra
;HDF HBF HDE HCE= =
Mà
HBF HCE=
(cùng phụ với góc
A
)
Nên:
HDF HDE=
0,25
Vậy
DH
là tia phân giác của
EDF
.
0,25
2) Chứng minh:
HE NC
HF NB
=
.
1,0
Ta có:
NC AC⊥
nên
// .NC BH
Tương tự, ta có
// .NB CH
Suy ra
BHCN
là hình bình hành.
0,25
Tứ giác
BCEF
nội tiếp, suy ra:
FEH BCH
=
và
FBH ECH
=
nên hai tam giác
HFE∆
∽
HBC∆
.
0,25
Do đó, hai tam giác
HFE∆
∽
NCB∆
.
0,25
Suy ra
.
HE NB
HF NC
=
0,25
Trang 5/5
3) Chứng minh:
.. ..HE MQ HB HF MP NC=
1,0
//MQ NC
(cùng vuông góc với
AC
)
MQ AM
NC AN
⇒=
//MP NB
(cùng vuông góc với
AB
)
MP AM
NB AN
⇒=
0,25
.
MQ MP NB MP
NC NB NC MQ
=⇒=
0,25
Mà
HE NB
HF NC
=
, suy ra
. ..
HE MP
HE MQ HF MP
HF MQ
=⇒=
0,25
Lại có
HB NC
=
(do
HBNC
là hình bình hành).
Vậy:
.. ..HE MQ HB HF MP NC=
0,25
------------------------------------------------- HẾT ------------------------------------------------
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 TỈNH TIỀN GIANG
TRUNG HỌC PHỔ THÔNG NĂM HỌC 2022-2023
ĐỀ THI CHÍNH THỨC
Môn thi: TOÁN (CHUYÊN TOÁN)
Thời gian làm bài: 150 phút
(Đề thi có 01 trang, gồm 04 bài)
(Không kể thời gian phát đề) Ngày thi: 18/6/2022.
--------------------------------------------------------------------------------------------------------------------
Bài 1. (3,0 điểm)
1) Rút gọn các biểu thức: 1 1 1 1 1 M = + + ++ + ; 1 + 2 2 + 3 3 + 4 14 + 15 15 + 16 ( − )3 2 3 1 6 3 +10 N = ( . 10 − 2) 3+ 5 2) Giải phương trình ( 2 + x x + )( 2 1 3 9 1
9x +1 − 3x) =1. 2
2x + xy +1= 4x
3) Giải hệ phương trình  . 3 2
x + x y + y = 3x Bài 2. (3,0 điểm)
1) Trong mặt phẳng tọa độ Oxy , cho parabol (P) 2
: y = ax qua M ( 3;3) và đường thẳng (d ) 1
: y = − x + m (với m là tham số). Xác định phương trình của parabol (P) , từ đó 2
tìm tất cả các giá trị của tham số m để đường thẳng (d ) cắt parabol (P) tại hai điểm
phân biệt A(x y B x y khác gốc tọa độ, sao cho y y A B 25 + = . A; A ) , ( B; B ) x x B A 16
2) Gọi x , x là hai nghiệm của phương trình 2
x + mx +1 = 0 và x , x là hai nghiệm của 1 2 3 4 phương trình 2
x + nx +1 = 0 , với ,
m n là các tham số thỏa mãn m ≥ 2 , n ≥ 2 .
Chứng minh rằng: (x − x )(x − x )(x + x )(x + x ) 2 2 = n − m . 1 3 2 3 1 4 2 4
3) Cho hai số x, y liên hệ với nhau bởi đẳng thức 2 2
x + 2y − 2xy +10(x − y) + 21 = 0.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S = x − y + 2. Bài 3. (1,0 điểm)
Tìm tất cả các cặp số nguyên ( ; x y) thỏa mãn 2x −1 y = . 2 x − x +1 Bài 4. (3,0 điểm)
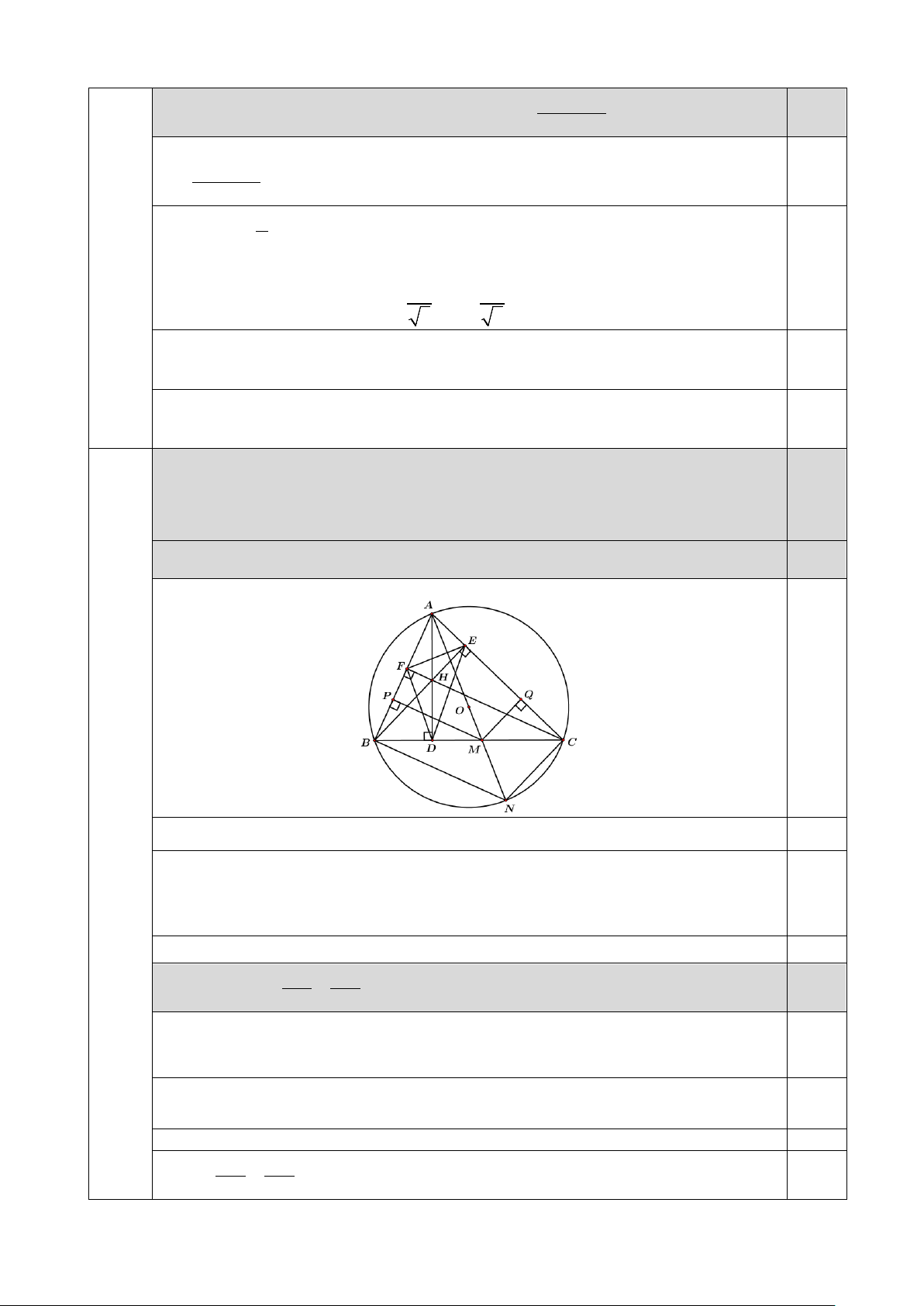
Cho tam giác nhọn ABC ( AB < AC) nội tiếp đường tròn tâm O , có ba đường cao
AD, BE,CF (D∈ BC, E ∈ AC, F ∈ AB) cắt nhau tại H. Tia AO cắt BC tại M và cắt (O) tại
N ; gọi P,Q lần lượt là hình chiếu của M trên AB, AC. Chứng minh:
1) DH là tia phân giác của  EDF . 2) HE NB = . HF NC 3) HE.M .
Q HB = HF.M . P NC .
----------------------------------------------------- HẾT ------------------------------------------------------
Thí sinh được sử dụng các loại máy tính cầm tay do Bộ Giáo dục và Đào tạo cho phép.
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không được giải thích gì thêm.
Họ và tên thí sinh: ..................................................... Số báo danh: ...................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 TỈNH TIỀN GIANG
TRUNG HỌC PHỔ THÔNG NĂM HỌC 2022-2023
Môn thi: TOÁN (CHUYÊN TOÁN)
ĐÁP ÁN ĐỀ THI CHÍNH THỨC
(Đáp án có 05 trang)
--------------------------------------------------------------------------------------------------------------------- I. Hướng dẫn chấm thi:
- Cán bộ chấm thi chấm 2 vòng độc lập.
- Cán bộ chấm thi không tự ý thay đổi thang điểm trong đáp án.
- Mọi cách giải khác, nếu đúng vẫn ghi đủ điểm.
II. Đáp án và thang điểm: Bài Nội dung Điểm 1
1) Rút gọn các biểu thức: 1,0 (3,0đ) 1 1 1 1 1 M = + + ++ + ; 1 + 2 2 + 3 3 + 4 14 + 15 15 + 16
M = 2 − 1 + 3 − 2 + 4 − 3 ++ 15 − 14 + 16 − 15 0,25 M = 16 −1 = 3 0,25 2( 3 − )1 6 3 +10 ( − ) ( + )3 3 3 2 3 1 3 1 N = ( = 0,25 10 − 2) 3+ 5 ( 5− )1 6+2 5 2( 3 − )1( 3 + )1 4 N = ( = = 0,25 5 − )1( 5 + ) 1 1 4 2) Giải phương trình ( 2 + x x + )( 2 1 3 9 1
9x +1 − 3x) =1 1,0 2 1+ 3x 9x +1 =1 2 2
⇔ 1+ 3x 9x +1 = 9x +1 + 3x 0,25 2 9x +1 + 3x ⇔ ( x − )( 2 3 1 9x +1 − )1 = 0 0,25 ⇔ 3x −1 = 0 hoặc 2 9x +1 −1 = 0 0,25 1
⇔ x = hoặc x = 0 . Vậy 1 S 0;  = 3 3 0,25   Cách khác: ( 2 + x x + )( 2 x + − x) = ( 2 x + − x)( 2 1 3 9 1 9 1 3 9 1 3 9x +1 + 3x) 0,25 Trang 1/5 2 2
⇔ 1+ 3x 9x +1 = 9x +1 + 3x 0,25 2
⇔ 9x +1 − 3x = 0 (vô nghiệm) hoặc ( x − )( 2 3 1 9x +1 − )1 = 0 ⇔ 3x −1 = 0 hoặc 2 9x +1 −1 = 0 0,25 1
⇔ x = hoặc x = 0 0,25 3 Vây 1 S 0;  =  3   2
2x + xy +1= 4x
3) Giải hệ phương trình  1,0 3 2
x + x y + y = 3x
Ta có (0; y) không là nghiệm của hệ nên hệ phương trình đã cho được viết lại:  1 2x + y + = 4  x   2 y x + xy + = 3  x 0,25 (   x y)  1 x  + + + =   4   x  ⇔  0,25 (  x + y) 1 x  + =   4   x  x + y = 2  ⇔  1 x + = 0,25  2 xx =1 ⇔ 
. Vậy hệ có tập nghiệm S = ( { 1; )1}. 0,25 y = 1 2
1) Trong mặt phẳng tọa độ Oxy , cho parabol (P) 2
: y = ax qua M ( 3;3) và (3,0đ) đường thẳng (d ) 1
: y = − x + m (với m là tham số). Xác định phương trình của 2
parabol (P) , từ đó tìm tất cả các giá trị của tham số m để đường thẳng (d ) cắt 1,25
parabol (P) tại hai điểm phân biệt A(x y B x y khác gốc tọa độ, sao cho A; A ) , ( B; B ) y y A B 25 + = . x x B A 16 M (
)∈(P) y = ax ⇔ = a( )2 2 3;3 : 3 3 ⇔ a =1 0,25 Vậy parabol (P) 2 : y = x 0,25 Trang 2/5
Phương trình hoành độ giao điểm của (P) và (d ): 2 1
x = − x + m 2 2
⇔ 2x + x − 2m = 0 có ∆ =1+16m
Để đường thẳng (d ) cắt parabol (P) tại hai điểm phân biệt A(x y B x y A; A ) , ( B; B ) khác gốc tọa độ 1 ⇔ m > − và m ≠ 0 . 16 0,25
Theo định lý Vi-et, ta có: 1 x + x = − x x = −m A B , A. 2 B 2 2 3 3 y y x x x + x A B 25 A B 25 A B 25 + = ⇔ + = ⇔ = x x x x x x B A 16 B A 16 A. B 16 0,25 3  1   1  ( − − −m x x x x x x −     + − + A B )3
3 A. B ( A B ) 3( ) 25  2   2  25 ⇔ = ⇔ = x x −m A. B 16 16 1 3 − − m 8 2 25 ⇔ = ⇔ 2 − − 24m = 25 − m −m 16
⇔ m = 2 (thỏa điều kiện). 0,25
2) Gọi x , x là hai nghiệm của phương trình 2
x + mx +1 = 0 và x , x là hai 1 2 3 4
nghiệm của phương trình 2
x + nx +1 = 0 , với ,
m n là các tham số thỏa mãn 0,75
m ≥ 2 , n ≥ 2 . Chứng minh rằng : (x − x )(x − x )(x + x )(x + x ) 2 2 = n − m . 1 3 2 3 1 4 2 4
x + x = −m
x + x = −n
Theo định lý Vi-et, ta có : 1 2  và 3 4 x x =   1 x x =  1 1 2 3 4 0,25
Ta có: VT = (x − x x − x x + x x + x 1 3 ) ( 2 3 ) ( 1 4 ) ( 2 4 )
= x x − x (x + x ) 2
+ x  x x + x (x + x ) 2 + x   1 2 3 1 2 3   1 2 4 1 2 4  = ( 2 1+ mx + x )( 2 1− mx + x 3 3 4 4 ) 0,25
= (mx − nx −mx − nx 3 3 ) ( 4 4 )
= (n − m) x m + n x 3 ( ) 4 2 2
= n − m = VP . 0,25
3) Cho hai số thực x, y liên hệ với nhau bởi đẳng thức 2 2
x + 2y − 2xy +10(x − y) + 21 = 0. Tìm giá trị lớn nhất và giá trị nhỏ nhất của 1,0
biểu thức S = x − y + 2.
Viết lại biểu thức đã cho thành (x − y + )2 + (x − y + ) 2 2 6 2 + 5 = −y . 0,25
Như vậy với mọi x và mọi y ta luôn có 2
S + 6S + 5 ≤ 0 (với S = x − y + 2) 0,25
Suy ra: (S + 5)(S + ) 1 ≤ 0 ⇔ 5 − ≤ S ≤ 1 − . Do đó: 0,25 x = 7 −
Giá trị nhỏ nhất của S bằng 5 − khi  y = 0 0,25 x = 3 −
Giá trị lớn nhất của S bằng 1 − khi  . y = 0 Trang 3/5 3 2x −1
(1,0đ) Tìm tất cả các cặp số nguyên ( ;
x y) thỏa mãn y = . 1,0 2 x − x +1 Ta có: 2x−1 y = 2
⇔ yx − ( y + 2) x + y +1 = 0. 0,25 2 x − x +11
y = 0 ⇒ x = (không thỏa). 2
y ≠ 0 , phương trình có nghiệm khi và chỉ khi
∆ = ( y + )2 − y( y + ) 2 2 2 4 1 ≥ 0 ⇔ − ≤ y ≤ . 3 3 0,25
Vì y ∈ và y ≠ 0 nên y ∈{ 1; − } 1 . 2
y =1⇒ x − 3x + 2 = 0 ⇔ x =1 hoặc x = 2 . 0,25 2 y = 1
− ⇒ x + x = 0 ⇔ x = 1 − hoặc x = 0 .
Vậy có 4 cặp số cần tìm là (1; ) 1 ,(2; ) 1 ,( 1 − ;− ) 1 ,(0;− ) 1 . 0,25 4
Cho tam giác nhọn ABC ( AB < AC) nội tiếp đường tròn tâm O, có ba đường cao
(3,0đ) AD,BE,CF (D∈BC,E∈ AC,F ∈ AB) cắt nhau tại H. Tia AO cắt BC tại M 3,0
và cắt (O) tại N, gọi P,Q lần lượt là hình chiếu của M trên AB, AC.
1) Chứng minh: DH là tia phân giác của  EDF . 1,0 Hình vẽ 0,25
Chứng minh đúng hai tứ giác BFHD,CEHD nội tiếp. 0,25 Suy ra  =   = 
HDF HBF; HDE HCE Mà  = 
HBF HCE (cùng phụ với góc A ) Nên:  =  HDF HDE 0,25
Vậy DH là tia phân giác của  EDF . 0,25 2) Chứng minh: HE NC = . 1,0 HF NB
Ta có: NC ⊥ AC nên NC//BH.
Tương tự, ta có NB//CH.
Suy ra BHCN là hình bình hành. 0,25
Tứ giác BCEF nội tiếp, suy ra:  =  FEH BCH và  = 
FBH ECH nên hai tam giác HF ∆ E ∽ HB ∆ C . 0,25
Do đó, hai tam giác HF ∆ E ∽ NCB ∆ . 0,25 Suy ra HE NB = . 0,25 HF NC Trang 4/5
3) Chứng minh: HE.M .
Q HB = HF.M . P NC 1,0
MQ//NC (cùng vuông góc với AC ) MQ AM ⇒ = NC AN 0,25
MP//NB (cùng vuông góc với AB ) MP AM ⇒ = NB AN MQ MP NB MP = ⇒ = . NC NB NC MQ 0,25 Mà HE NB = , suy ra HE MP =
⇒ HE.MQ = HF. . MP HF NC HF MQ 0,25
Lại có HB = NC (do HBNC là hình bình hành). Vậy: HE.M .
Q HB = HF.M . P NC 0,25
------------------------------------------------- HẾT ------------------------------------------------ Trang 5/5
Document Outline

  • 57. TIỀN GIANG. ĐỀ
  • 57. TIỀN GIANG. ĐA