



Preview text:
SỞ GIÁO DỤC, KHOA HỌC
KỲ THI TUYỂN SINH LỚP 10 NĂM HỌC 2022-2023
VÀ CÔNG NGHỆ BẠC LIÊU
Môn thi: TOÁN (KHÔNG CHUYÊN) ĐỀ CHÍNH THỨC
Thời gian: 120 phút (không kể thời gian phát đề) Ngày thi: 10/06/2022 HƯỚNG DẪN GIẢI
Câu 1. (4 điểm) Rút gọn biểu thức a) A = 5 + 20 + 45 . b) 1 1 B = − (a a +
a), với a > 0. a a +1 Lời giải
Câu 1. (4 điểm) Rút gọn biểu thức a) A = 5 + 20 + 45 . Ta có A = 5 + 20 + 45 = 5 + 4⋅5 + 9⋅5 = 5 + 2 5 + 3 5 = 6 5 b) 1 1 B = − (a a +
a), với a > 0. a a +1 Ta có 1 1 B = − (a a + a) a a +1 a 1 a + − = + a ( a + ) (a a a) 1 a a + a = a ( a + ) 1 a( a + )1 = a( a + )1 = a. Câu 2. (4 điểm) x + y = 3
a) Giải hệ phương trình 3 x − y = 5 b) Cho parabol (P) 2
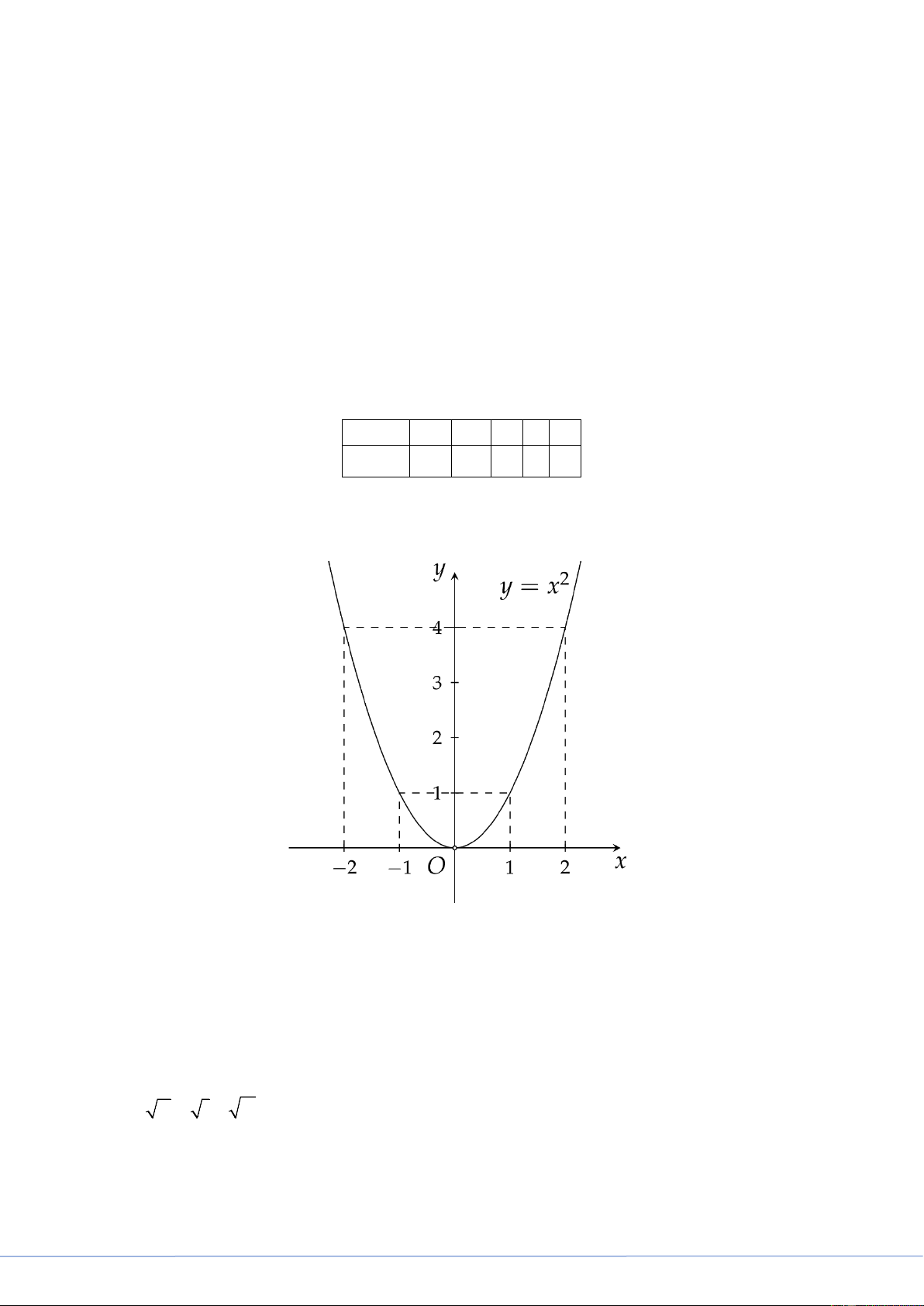
: y = x và đường thẳng (d ): y = 3x − 2. Vẽ đồ thị (P) và tìm tọa độ giao
điểm của (P) với đường thẳng (d ) bằng phép tính. Trang 2 Lời giải x + y = 3
a) Giải hệ phương trình 3 x − y = 5 Ta có x + y = 3 4x = 8 x = 2 ⇔ ⇔ 3 x y 5 x y 3 − = + = y =1
Vậy hệ phương trình có nghiệm ( ; x y) = (2; ) 1 . Tập xác định:
b) Bảng giá trị của (P) x 2 − 1 − 0 1 2 2 y = x 4 1 0 1 4
Vẽ đồ thị hàm số (P)
Phương trình hoành độ giao điểm của (D) và (P) : 2 x = 3x − 2 2
⇔ x − 3x + 2 = 0 ∆ = 1 2 ∆ = 1 = 1 =1 ⇔ x = 2 hay 1 x = x = ⇒ y = ( )2 2 2 = 4 Trang 3 x = ⇒ y = ( )2 1 1 =1
Vậy toạ độ giao điểm của (D) và (P) là: (2;4)và (1; ) 1 Câu 3. (6 điểm) Cho phương trình 2
x − 5x + m + 2 = 0 ( ) 1 ( m là tham số).
a) Giải phương trình khi m = 2 .
b) Tìm điều kiện của m để phương trình ( )
1 có hai nghiệm phân biệt.
c) Gọi x ,x là hai nghiệm phân biệt của phương trình ( )
1 . Tìm giá trị lớn nhất của biểu thức 1 2 2 2 2 2
P = x x + x x − x x − 4. 1 2 1 2 1 2 Lời giải
a) Thay m = 2 vào phương trình ( ) 1 ta được 2
x − 5x + 4 = 0 .
Do a + b + c =1+ ( 5)
− + 4 = 0 nên phương trình có hai nghiệm x =1;x = 4 . 1 2
b) Ta có ∆ =17 − 4m . Phương trình ( )
1 có hai nghiệm phân biệt khi và chỉ khi ∆ > 0 ⇔ 17 − 4m > 0 17 ⇔ m < . 4
c) Theo câu b, phương trình có hai nghiệm phân biệt khi 17 m < . 4 x + x = 5
Theo hệ thức Vi-ét, ta có 1 2 (1)
x ⋅ x = m + 2. 1 2 Theo đề ta có
P = x x + x x − x x − 4 = x x (x + x ) −(x x )2 2 2 2 2 − 4. 1 2 1 2 1 2 1 2 1 2 1 2 Thay ( ) 1 vào ta được
P = 5(m + 2) − (m + 2)2 − 4 2
= 5m +10 − m − 4m −8 2 = −m + m + 2 2 1 9 9 = − m − + ≤ . 2 4 4 9 1 1
P = ⇔ m − = ⇔ m = (thỏa mãn điều kiện) max 0 4 2 2 Câu 4. (6 điểm)
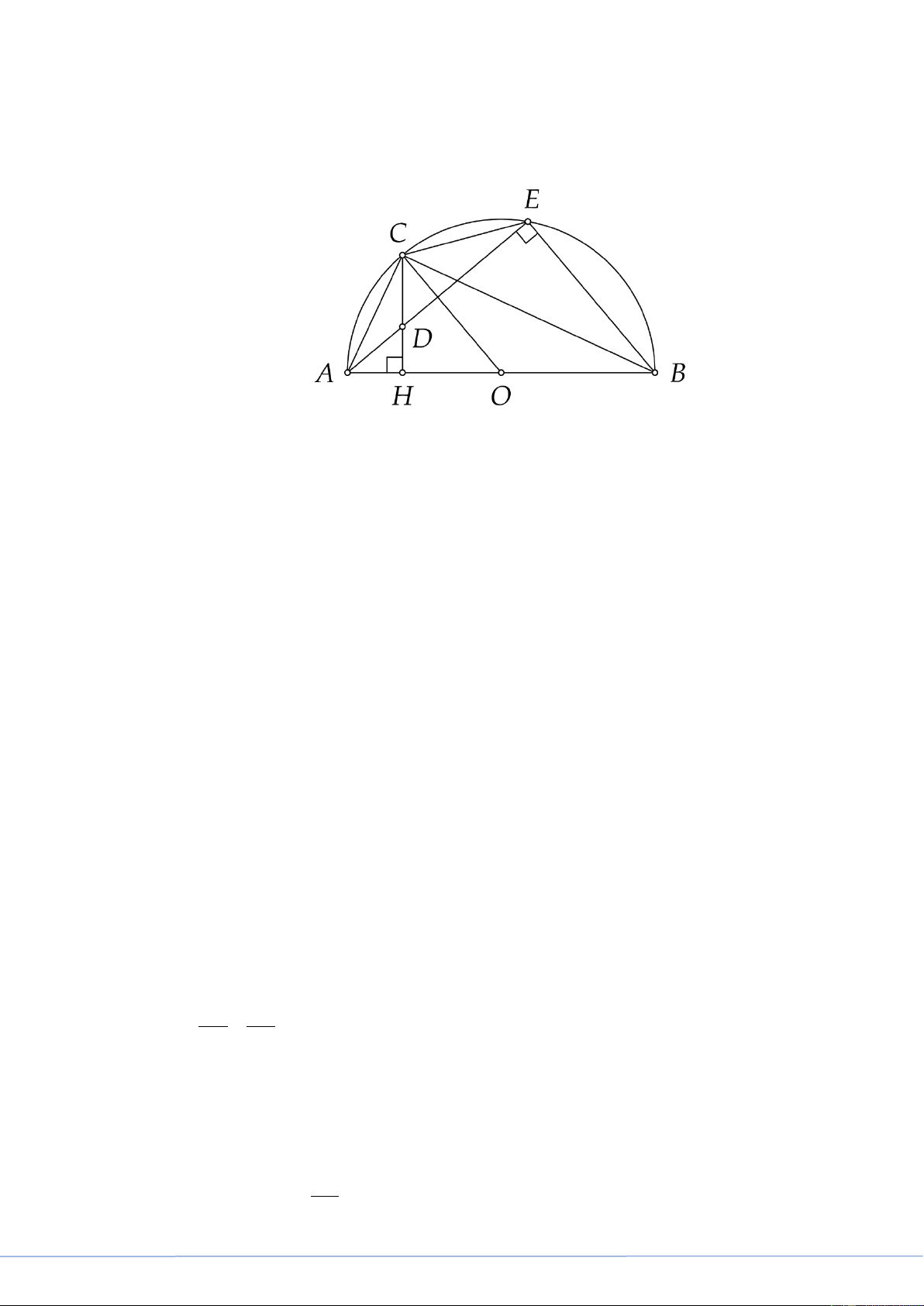
Trên nửa đường tròn tâm O đường kính AB = 2R , lấy điểm C (C khác A và B ), từ C kẻ
CH vuông góc với AB (H ∈ AB) . Gọi D là điểm bất kì trên đoạn CH (D khác C và H ),
đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E .
a) Chứng minh tứ giác BHDE nội tiếp.
b) Chứng minh AD ⋅ EC = CD ⋅ AC . Trang 4
c) Khi điểm C di động trên nửa đường tròn (C khác A , B và điểm chính giữa cung AB ), xác
định vị trí của điểm C sao cho chu vi C
∆ OH đạt giá trị lớn nhất. Lời giải
a) Chứng minh tứ giác BHDE nội tiếp.
Xét tứ giác BHDE , ta có ⊥ ⇒ CH AB(gt) BHD = 90° . và
AEB là góc nội tiếp chắn nửa đường tròn nên BED = 90° Suy ra BHD BED 180° + =
(tổng hai góc đối bằng 180°).
Do đó tứ giác BHDE nội tiếp (đpcm)
b) Chứng minh AD⋅ EC = CD⋅ AC .
và + = + = ° ⇒ = ACD CAH ABC CAH 90 ACD ABC . Mặt khác, ta có =
ABC CEA (hai góc nội tiếp cùng chắn cung CA ). Suy ra = ACD AEC . Xét A ∆ CD và A ∆ EC , ta có = CAD EAC (góc chung) =
ACD AEC (chứng minh trên) suy ra A ∆ CD ∽ A ∆ EC (g-g). Suy ra AD CD =
⇒ AD ⋅ EC = CD ⋅ AC (đpcm). AC EC
c) Khi điểm C di động trên nửa đường tròn (C khác A , B và điểm chính giữa cung AB ),
xác định vị trí của điểm C sao cho chu vi C
∆ OH đạt giá trị lớn nhất.
Gọi P chu vi tam giác COH , ta có AB
P = CO + OH + CH = + OH + CH. 2 Trang 5
Áp dụng bất đẳng thức (a + b)2 2 2
≤ 2(a + b ) với các đoạn thẳng OH , CH , ta có (OH +CH )2 2 2 2
≤ 2(OH + CH ) = 2OC . Suy ra + ≤ 2 AB OH CH OC = 2 = R 2 . 2 Do đó, AB AB P = + OH + CH ≤
+ R 2 = R + R 2 . 2 2
Chu vi tam giác COH lớn nhất khi OH = CH .
Vậy C nằm trên nửa đường tròn sao cho tam giác COH là tam giác vuông cân.
_____ THCS.TOANMATH.com _____ Trang 6
Document Outline
- de-tuyen-sinh-lop-10-mon-toan-khong-chuyen-nam-2022-2023-so-gdkhcn-bac-lieu
- 4.BẠC LIÊU




