Đề tuyển sinh lớp 10 môn Toán năm 2018 – 2019 sở GD và ĐT Tiền Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 TỈNH TIỀN GIANG Năm học 2018-2019 ĐỀ THI CHÍNH THỨC Môn thi: TOÁN
(Đề thi có 01 trang, gồm 05 bài)
Thời gian làm bài: 120 phút
(không kể thời gian phát đề) Ngày thi: 05/6/2018
 Bài I. (3,0 điểm) 1
1. Tính giá trị của biểu thức: A  4  2 3  12 . 2
2. Giải phương trình và hệ phương trình sau:
3x  y  11 a/ 4 2
x  x  20  0 b/  . 2x  y  9  3. Cho phương trình 2
x  2x  5  0 có hai nghiệm x , x . Không giải phương trình, hãy tính giá trị 1 2 của các biểu thức: 2 2
B  x  x ; 5 5
C  x  x . 1 2 1 2 Bài II. (2,0 điểm) 1
Trong mặt phẳng tọa độ Oxy cho parabol P  2
: y  x và đường thẳng d  : y  x  m . 2
1. Vẽ P  và d  trên cùng một mặt phẳng tọa độ khi m  2.
2. Định các giá trị của m để d  cắt P  tại hai điểm phân biệt A và B .
3. Tìm giá trị của m để độ dài đoạn thẳng AB  6 2 .
Bài III. (1,5 điểm)
Hai bến sông A và B cách nhau 60 km. Một ca nô đi xuôi dòng từ A đến B rồi ngược dòng từ B
về A . Thời gian đi xuôi dòng ít hơn thời gian ngược dòng là 20 phút. Tính vận tốc ngược dòng của ca nô,
biết vận tốc xuôi dòng lớn hơn vận tốc ngược dòng của ca nô là 6 km/h. Bài IV. (2,5 điểm)
Cho tam giác ABC có ba góc nhọn AB  AC  , các đường cao AF , BD , CE cắt nhau tại H .
1. Chứng minh tứ giác BEDC nội tiếp trong một đường tròn.
2. Chứng minh AE.BD  AD.AC .
3. Chứng minh FH là tia phân giác của  EFD .
4. Gọi O là trung điểm của đoạn thẳng BC . Chứng minh   DOC  FED . Bài V. (1,0 điểm) 1
Một hình trụ có diện tích xung quanh bằng 2
256 cm và bán kính đáy bằng đường cao. Tính 2
bán kính đáy và thể tích hình trụ.
HẾT HƯỚNG DẪN GIẢI Bài I. (3,0 điểm) 1. A    2
3 1  3  3  1  3  1  . 2. a/ 4 2
x  x  20  0 , (1) Đặt 2
x  t, điều kiện t  0 .
Khi đó phương trình trở thành: 2
t  t  20  0 , (2) Ta có 2   1  4.1. 2
 0  81  0 nên phương trình (2) có hai nghiệm phân biệt: 1   9 t   4 (nhận) 1 2.1 1   9 t   5  (loại) 1 2.1 Với 2
t  4  x  4  x  2  .
Vậy tập nghiệm của phương trình (1) là S   2;  2.
3x  y  11
3x  y  11
3x  y  11 y   1 b/        . 2x  y  9 5x  20 x  4 x  4    
Vậy nghiệm của hệ phương trình là x;y  4;1. 3. 2
x  2x  5  0
Ta có a.c  1. 5    5
  0 nên phương trình luôn có hai nghiệm x , x . 1 2
Theo hệ thức Vi-et ta có: S  x  x  2; P  x x  5  . 1 2 1 2 Ta có: 2 2 2 2
B  x  x  S  2P  2  2 5   14 . 1 2   Mặt khác:
x  x 2  x  x  2x .x  x  x  x  x 2 2x .x  S 2P2 2 2 4 4 2 2 4 4 2 2 2 2 2 2 4 2 2
 2P  S  4S P  2P 1 2 1 2 1 2 1 2 1 2 1 2 Nên 5 5
C  x  x  x  x  4 3 2 2 3 4
x  x x  x x  x x  x 1 2 1 2 1 1 2 1 2 1 2 2 
 x  x  4 4 2 2 3 3
x  x  x x  x x  x x   x  x  4 4 2 2
x  x  x x  x x  2 2 x  x 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2   S  4 2 2 2
S  S P  P  P  P  2
S  P   S  4 2 2 4 2 2
S  5S P  5P       2 4 2 2 2 5.2 . 5 5. 5         482 .   Bài II. (2,0 điểm) 1
Trong mặt phẳng tọa độ Oxy cho parabol P  2
: y  x và đường thẳng d  : y  x  m . 2
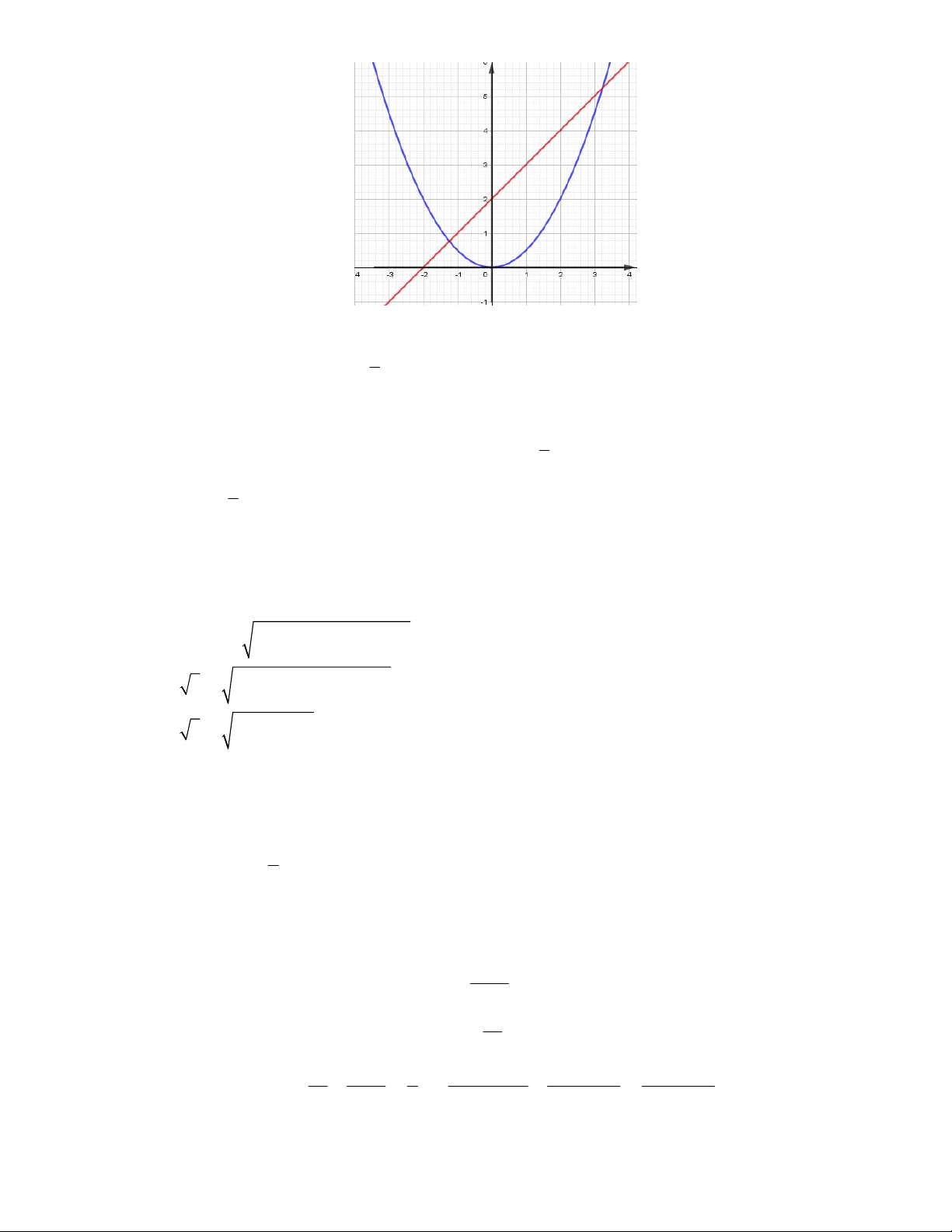
1. Khi m  2 , d  : y  x  2. x 2  1  0 1 2  2  1 0 1 2 P  1 2 : y  x 2 2 2 x 0 1
d : y  x  2 2 3 y P x O d
2. Phương trình hoành độ giao điểm của d  và P  có dạng 1 2
 x  m  x  2x  2m  0,1 2
d cắt P tại hai điểm phân biệt A và B khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt
    2   m 1 1 1. 2
 0  1  2m  0  m   . 2 1
Vậy m   thì d  cắt P  tại hai điểm phân biệt A và B . 2
3. Gọi Ax ;y ,B x ;y , 1 1   2 2
với x ,x là nghiệm của phương trình (1) thỏa S  x  x  2;P  x .x  2m 1 2 1 2 1 2
y  x  m; y  x  m . 1 1 2 2 2 2
Ta có: AB  x  x  y  y 2 1   2 1
 6 2  x  x 2  x  x 2 2 1 2 1  2 2
6 2  2 x  x 2  72  2x  x
 36  x  x 2 1   2 1 2 1 2 2
 36  x  x  2x x 2 2
 36  S  2P  2P  36  S  4P 2 1 2 1 2  36  2  4  2
 m   m  4 .
Bài III. (1,5 điểm) 1 Ta có 20 phút  giờ. 3
Gọi x km/h là vận tốc ngược dòng của ca nô. Điều kiện: x  0 .
Vận tốc xuôi dòng của ca nô là: x  6 km/h 60
Thời gian ca nô đi xuôi dòng từ A đến B là: h. x  6 60
Thời gian ca nô đi ngược dòng từ B đến A là: h. x 60 60 1 180 x  6 x x x  6 180  Ta có phương trình là:      x x  6 3
3x x  6 3x x  6 3x x  6
 180 x  6  180x  x x  6 2
 x  6x  108  0 .
Giải phương trình trên ta được: x  30 (nhận) và x  36  (loại).
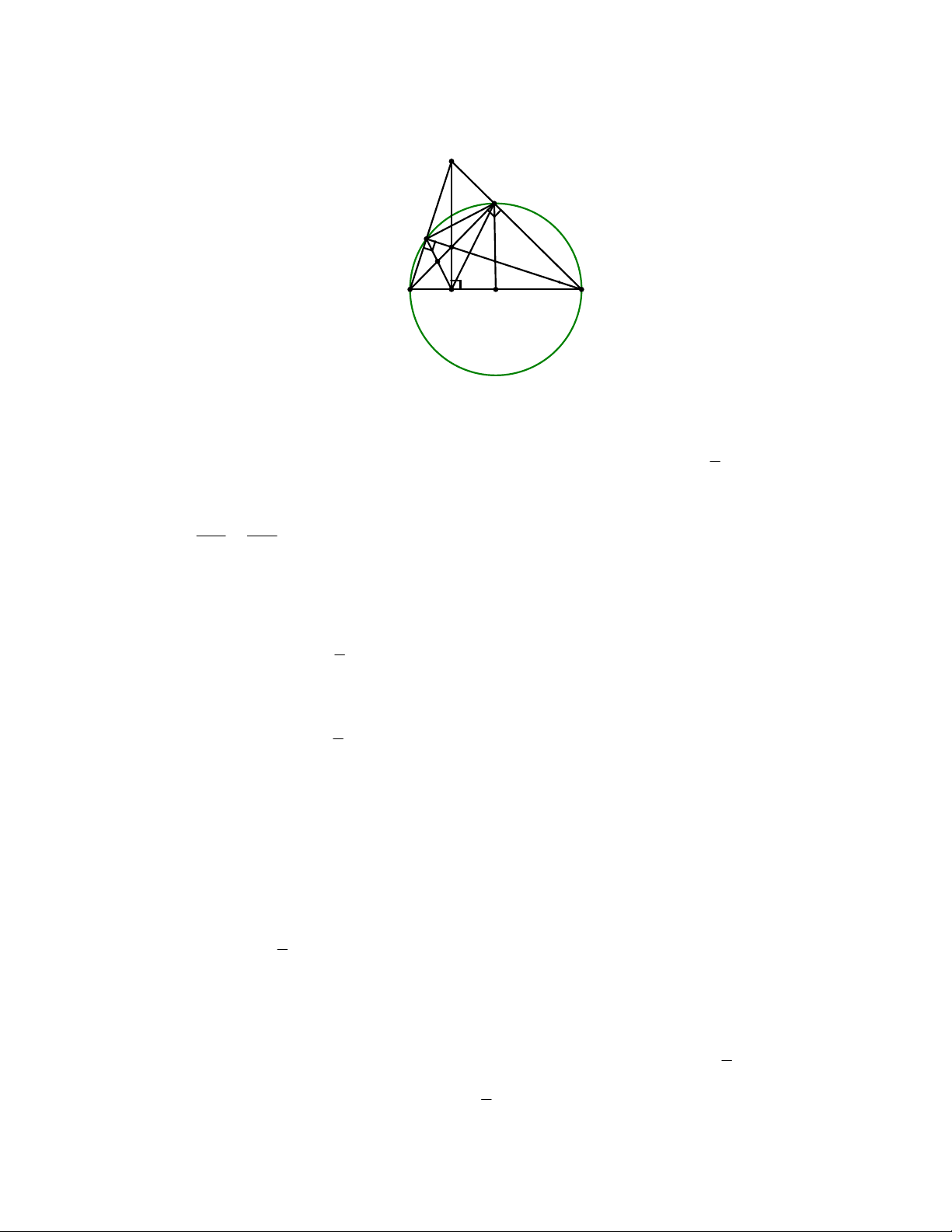
Vậy vận tốc ngược dòng của ca nô 30 km/h . Bài IV. (2,5 điểm) A D E H I B C F O 1. Ta có:  BEC  90 , 
BDC  90 và hai góc  
BEC,BDC cùng nhìn cạnh BC .
Vậy tứ giác BEDC nội tiếp trong một đường tròn.  1 
2. Xét hai tam giác AEC và tam giác ADB , có  A chung và   
ABD  ACE   s E ñ D  2   Vậy AE  C ~ A
 DB ( góc – góc). AE AC Suy ra 
 AE.BD  AD.AC . AD BD
Vậy AE.BD  AD.AC . 3. Ta có
+ HEBF nội tiếp một đường tròn ( do  
BEH  BFH  90 )  1  Nên   
BFE  BHE   s B ñ E  2  
+ CDHF nội tiếp một đường tròn ( do  
CDH  CFH  90 )  1  Nên   
CFD  CHD   s C ñ D  2   Mà  
BHE  CHD nên   BFE  CFD   BF 
E  EFA  90 Mặt khác:   CFD   DFA  90  Do đó  
EFA  DFA . Vậy FH là tia phân giác của  EFD . 4. Ta có   DOC  s C ñ D (1) 1 Mặt khác   DEC  s C ñ D (*) 2
Gọi I là giao điểm của BH và EF .    
IEH  EIH  EHI  180  1 Ta có:    IB
 F  BIF  IFB  180 . Suy ra:   
IEH  IBF  s C ñ D (**)  2      1   EI
 H  BIF(ñoái ñæ )
nh ;EHI  IFB   s E ñ B   2    Từ (*) và (**), suy ra:    
FED  DEC  IEH  s CD ñ (2) Từ (1) và (2) suy ra   DOC  FED .
Bài V. (1,0 điểm) 1
Ta có: r  h  h  l  2r 2
Diện tích xung quanh hình trụ là: 2 2 S  2 r
 l  256 cm  2 r
 .2r  256  r  64  r  8 cm . xq
Suy ra: h  l  2.8  16 cm . Thể tích hình trụ: 2 2 3 V  r  h  .8  .16  1024 cm .
Vậy hình trụ có bán kính đáy là r  8 cm và thể tích 3 V  1024 cm .