



Preview text:
SỞ GD&ĐT QUẢNG BÌNH
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2021 - 2022 ĐỀ CHÍNH THỨC Khóa ngày 08/6/2021 Môn: TOÁN (CHUNG)
SBD:………….. Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Đề có 01 trang gồm 5 câu MÃ ĐỀ 001 Câu 1 (2,0 điểm).
Rút gọn các biểu thức sau: a) A 8 32 50. a a a a b) B 3 3 (với a 0, a 1). a 1 a 1 Câu 2 (1,5 điểm).
a) Tìm tất cả các giá trị của m để hàm số y m
1 x 2 đồng biến trên . 3 x 2 y 8
b) Giải hệ phương trình . 3 x 4y 2 Câu 3 (2,0 điểm). Cho phương trình 2 x 6x m 4 0
1 (với m là tham số).
a) Giải phương trình (1) khi m 1.
b) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm x , x thỏa mãn 1 2
2020 x x 2021x x 2014. 1 2 1 2 Câu 4 (1,0 điểm). a b 1
Cho a, b là các số thực dương. Chứng minh .
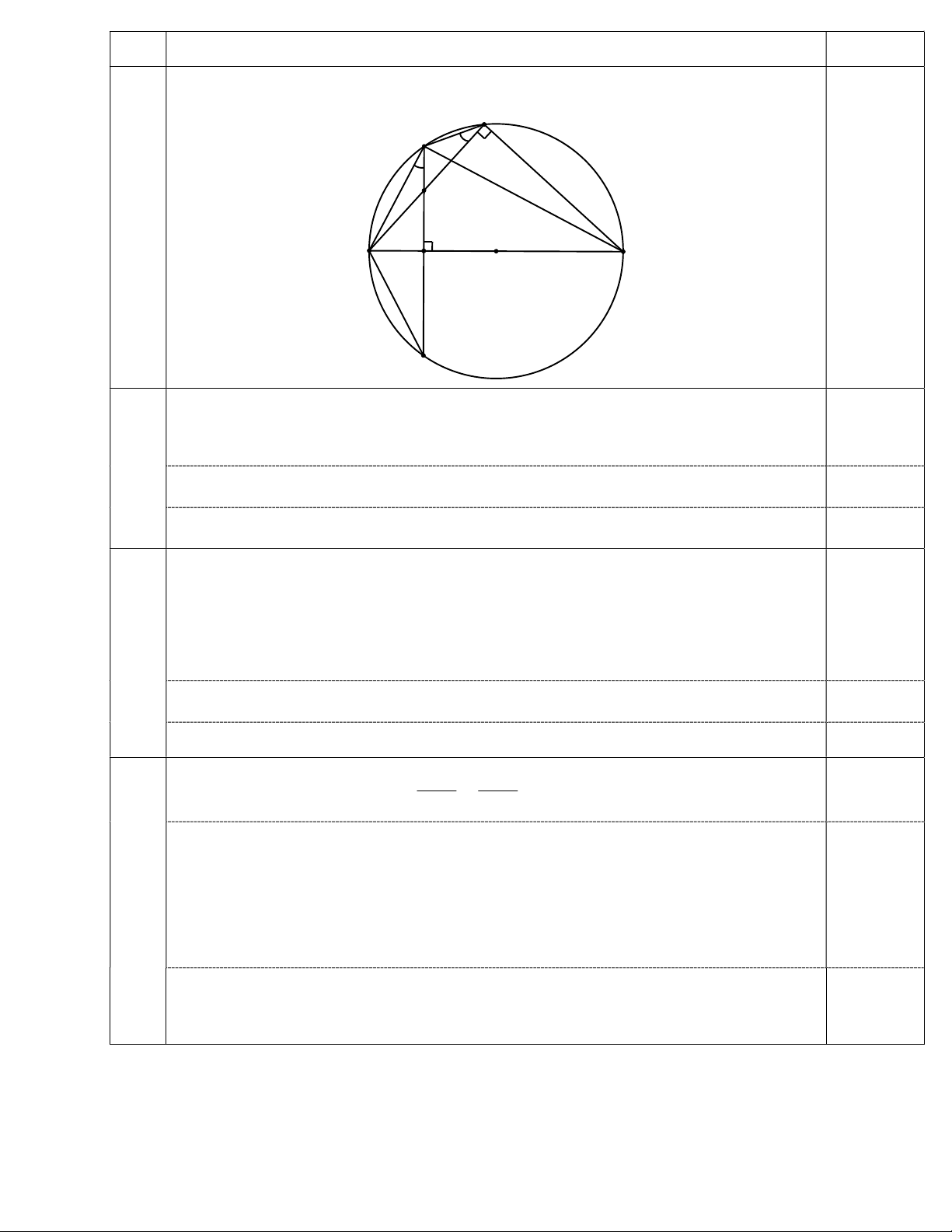
a15a b b15b a 4 Câu 5 (3,5 điểm). Cho đường tròn ; O R đường kính A ,
B dây cung MN vuông góc với AB tại I
sao cho AI BI. Trên đoạn thẳng MI lấy điểm H ( H khác M và I ), tia AH cắt đường tròn ;
O R tại điểm thứ hai là K. Chứng minh rằng:
a) Tứ giác BIHK nội tiếp đường tròn. b) A HM đồng dạng với A MK. c) 2 AH.AK BI.AB 4R .
...........................HẾT......................... SỞ GD&ĐT QUẢNG BÌNH HƯỚNG DẪN CHẤM
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2021 -2022 Khóa ngày 08/6/2021 Môn: TOÁN (CHUNG)
(Hướng dẫn chấm gồm có 04 trang) Yêu cầu chung
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu
phải lập luận logic chặt chẽ, đầy đủ, chi tiết rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với những bước sau có liên quan.
* Điểm thành phần của mỗi câu được phân chia đến 0,25 điểm. Đối với điểm là 0,5
điểm thì tùy tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Đối với Câu 5, học sinh không vẽ hình thì cho điểm 0. Trường hợp học sinh có vẽ
hình, nếu vẽ sai ở ý nào thì điểm 0 ở ý đó.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tùy theo mức điểm từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm
Rút gọn các biểu thức sau: a) A 8 32 50 . 1 2,0 điểm a a a a b) B 3 3 (với a 0, a 1). a 1 a 1
Ta có: A 2 2 4 2 5 2 0,5 a 3 2 . 0,5
Với a 0, a 1 ta có: a a 1 a a 1 b 0,5 B 3 3 a 1 a 1
3 a 3 a 0,25 9 a . 0,25 Vậy B 9 . a HDC Mã đề 001 Trang 1/4 Câu Nội dung Điểm
a) Tìm tất cả các giá trị của m để hàm số y m 1 x 2 đồng biến trên . 2 1,5 điểm 3 x 2 y 8
b) Giải hệ phương trình . 3 x 4y 2
Hàm số đã cho đồng biến trên khi và chỉ khi m 1 0 0,25 a m 1 0,25
Vậy với m 1 thì hàm số đồng biến trên . 3 x 2y 8 6y 6 Ta có 0,25 3 x 4y 2 3 x 2y 8 y 1 x 2 b 0,5 3 x 2 8 y 1
Vậy hệ phương trình có nghiệm là ; x y 2; 1 . 0,25 Cho phương trình 2 x 6x m 4 0
1 (với m là tham số).
a) Giải phương trình (1) khi m 1. 3 2,0 điểm
b) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm
x , x thỏa mãn 2020 x x 2021x x 2014. 1 2 1 2 1 2
Với m 1 ta có phương trình 2 x 6x 50 0,25
Vì a b c 1 (6) 5 0 nên phương trình có hai nghiệm là a 0,5 x 1; x 5. 1 2
Vậy với m 1 thì phương trình
1 có hai nghiệm là x 1; x 5. 1 2 0,25
Ta có ' 9 m 4 5 m Phương trình
1 có hai nghiệm ' 0 5 m 0 m 5. 0,25 x x 6
Theo hệ thức Vi-ét ta có: 1 2 x .x = m 4 1 2
2020(x x ) 2021x x 2014 2020.6 202 1 m 4 2014 0,25 1 2 1 2 b 2022
2022 2021m 0 m (thỏa mãn) 0,25 2021 2022 Vậy với m thì phương trình
1 có hai nghiệm x , x thỏa mãn: 2021 1 2 0,25
2020(x x ) 2021x x 2014. 1 2 1 2 HDC Mã đề 001 Trang 2/4 Câu Nội dung Điểm
Cho a, b là các số thực dương. Chứng minh 4 a b 1 . 1,0 điểm
a15a b b15b a 4 a b 4a b Ta có 1 0,25
a15a b b15b a
16a15a b 16b15b a
Áp dụng bất đẳng thức Cô-si ta có: a a b 16a 15a b 16 15 2. 2
Dấu bằng xảy ra khi và chỉ khi 16a 15a b a b 0,25 b b a 16b 15b a 16 15 3. 2
Dấu bằng xảy ra khi và chỉ khi 16b 15b a a . b
Từ (1), (2) và 3 ta được a b 4a b 8a b 1 0,5
a15a b b15b a 31a b 31b a 32a b 4 2 2
Dấu bằng xảy ra khi a b. Cho đường tròn ; O R đường kính A ,
B dây cung MN vuông góc với
AB tại I sao cho AI BI. Trên đoạn thẳng MI lấy điểm H ( H khác
M và I ), tia AH cắt đường tròn ;
O R tại điểm thứ hai là K. Chứng 5 minh rằng: 3,5 điểm
a) Tứ giác BIHK nội tiếp đường tròn. b) A HM đồng dạng với A MK. c) 2 AH.AK BI.AB 4R . HDC Mã đề 001 Trang 3/4 Câu Nội dung Điểm Hình vẽ K M H A O B I 0,5 N Ta có: 0
AKB 90 (góc nội tiếp chắn nửa đường tròn) 0,25 0 HKB 90 a Vì MN AB tại I nên 0 HIB 90 0,25 Tứ giác BIHK có HKB 0
HIB 180 nên tứ giác BIHK nội tiếp 0,5
Vì đường kính AB vuông góc với dây cung MN nên AB là đường trung
trực của đoạn thẳng MN. 0,5 Suy ra AM AN sđ AM sđ AN AMN AKM b Hay AMH AKM . Xét A HM và A MK có AMH AKM và MAK chung 0,25 Suy ra A HM ∽ A MK (g.g) 0,25 AH AM Từ A HM ∽ A MK suy ra 2 AM AH.AK 1 0,25 AM AK Ta có: 0
AMB 90 (góc nội tiếp chắn nửa đường tròn)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông AMB có 2 AM AI.AB 2 0,5 c Từ
1 và 2 suy ra AH.AK AI.AB
AH AK BI AB AI AB BI AB AB AI BI 2 2 . . . . AB 4R 0,25 Vậy 2 AH.AK BI.AB 4R . HDC Mã đề 001 Trang 4/4




