Đề tuyển sinh lớp 10 môn Toán năm 2022 – 2023 sở GD&ĐT Hậu Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT, THPT CHUYÊN TỈNH HẬU GIANG NĂM HỌC: 2022 - 2023 MÔN THI : TOÁN - THPT ĐỀ CHÍ
Thời gian làm bài : 90 phút, không tính thời gian phát đề NH THỨC (Đề thi gồm 02 trang)
I. Phần trắc nghiệm: (2,0 điểm)
Câu 1. Số nào sau đây la căn bậc hai số học của 4 ? A. 16 . B. 16 . C. 2 . D. 2 .
Câu 2. Rút gọn biểu thức 8  2 . A. 2 2 . B. 3 2 . C. 10 . D. 16 .
Câu 3. Giả sử x ,x là hai nghiệm của phương trình 2
x  4x 1  0. Giá trị của biểu thức 1 2 x  x bằng 1 2 A. 1. B. 1. C. 4 . D. 4 .
Câu 4. Tìm nghiệm của hệ phương trình x   3 x   2  x   3  x   2 A. . B. . C. . D. . y        2  y   3  y   2  y  3  
Câu 5. Phương trình x 4  x2
9  20  0 có bao nhiêu nghiệm? A. 4 . B. 2 . C. 0 . D. 1.
Câu 6. Tính diện tích S của hình cầu có bán kính R  a 2 . A. S  a2 16 . B. S  a2 8 . C. S  a2 4 . D. S  a2 2 .
Câu 7. Tính chu vi của đường tròn ngoại tiếp tam giác, biết tam giác ABC vuông tại A và BC  a 6 . A. 6a . B. 3a . C. 4a . D. 3a .
Câu 8. Cho hình thang có đáy lớn BC , đáy nhỏ AD , AD  BC  10cm, AC  5 2 cm và  ACB 45 
. Tính diện tích S của hình thang đã cho. 25 A. S  cm2 50 2 . B. S  cm2 . C. S  cm2 25 2 . D.S  cm2 25 . 2
II. Phần tự luận: (8,0 điểm) Câu 1. (2,0 điểm)
a) Tính giá trị đúng của biểu thức A  x  3  x 3  1 khi x  1. x  9
b) Rút gọn biểu thức B  , với x  0 . x  3
c) Tìm số thực x không âm thỏa mãn x  5 . a 2  2 a a  2 2 d) Cho biểu thức D   
, với 0  a  4 . Tìm a để D là số nguyên. a  4 a  2 a  2 Câu 2. (2,0 điểm)
a) Giải phương trình x2  x  12  0 .
b) Giải phương trình  x   x    x2 5 3 1  x 2  15  8 Câu 3. (1,5 điểm)
Trong mặt phẳng với hệ tọa độ Oxy , cho hàm số y x2
  có đồ thị P  và hàm số y   m 5  6x  1 m
5  25 có đồ thị là đường thẳng d , với m là tham số.
a) Vẽ đồ thị P  .
b) Tìm m để d cắt P  tại hai điểm phân biệt có hoành độ x , x thỏa mãn x  x  6 . 1 2 1 2 Câu 4. (2,0 điểm)
Cho đường tròn O có bán kính R  3 và điểm M sao cho OM  R
2 . Từ M , kẻ hai tiếp tuyến
MA,MB tới O, với A và B là hai tiếp điểm.
c) Chứng minh tứ giác MAOB nội tiếp. Tính diện tích S của tứ giác MAOB .
d) Lấy điểm C trên đường tròn O sao cho tam giác ABC nhọn, AB  AC và có các đường cao
BE, CF. Gọi H là trực tâm tam giác ABC và N, J lần lượt là trung điểm của BC, AH. Chứng
minh tứ giác AJNO là hình bình hành và  JEN 90  . Câu 5. (0,5 điểm) x  y  y2  y  y 2  1  x  y
Giải hệ phương trình  . x y 3  x 4 y2  x 7 y  x 5  y  19   0 
--------------------------------- HẾT ---------------------------------
ĐÁP ÁN PHẦN TRẮC NGHIỆM 1C 2B 3D 4D 5A 6A 7A 8D ĐÁP ÁN PHẦN TỰ LUẬN Câu 1. (2,0 điểm)
a) Thay x  1 vào biểu thức A  x  3  x 3  1
Ta được A  1  3  3.1  1  4  4  2  2  4.   2 x  2  3  x  3 x x  3 9  b) Ta có: B     x  3. x  3 x  3 x  3 2 c) x    x  2 5  5  x  25.     2 a  2 2 a a a a a a  2 2 2 2 2 2 2  d) Xét biểu thức D       a  4 a  2 a  2 a  4 a  4 a  4 a
2  2 a  a  4 a  4  2 a  4 a 3  4 a D   , với 0  a  4 . a  4 a  4 Câu 2. (2,0 điểm)
a) Giải phương trình x2  x  12  0 . 2 Ta có:    1    4.1. 1  2  49  0  1  49  1  49
 PT có hai nghiệm phân biệt x   4; x   3 . 1 2 2.1 2.1 Vậy S  4;  3 .
b) Giải phương trình  x   x    x2 5 3 1  x 2  15  8 * ĐK: x  3 a   x  5 Đặt 
a  b  0  a2 b2  8 và ab  x2  x2 15 . b   x  3 
PT    a  b  ab  a2  b2 * 1
 1  ab  a  b  a   1 1  b  0 a   1  x  4  L  
. Vậy phương trình có nghiệm duy nhất x  4. b   1  x  4  N  Câu 3. (1,5 điểm) a) Bảng giá trị x 2 1 0 1 2 y x2   4  1  0 1  4  Đồ thị y -2 -1 O 1 2 x -1 -4 b) Tìm m ...
Xét phương trình hoành độ giao điểm của P  và d : x2    m  x  m   x2 5 6 15 25   m 5  6x  1 m 5  25  0 1 2
Ta có:    m     m    m2 5 6 4. 15 25 25  64
Để d cắt P  tại hai điểm phân biệt có hoành độ x , x  PT 1 có hai nghiệm phân biệt 1 2     m2 64   m 8 0  * 25 5 x   x   m 5  6 Theo Vi-et, có: 1 2 x  x.  1 m 5   25  1 2 2 2
Xét x  x  6  x  x  36    4 .  36 1 2  x x 1 2  x x 1 2 1 2   m  2 5 6  4 1 m 5  25  36  m2 25  100  0  m  2  (Thỏa đk * ) Vậy m  2 . Câu 4. (2,0 điểm)
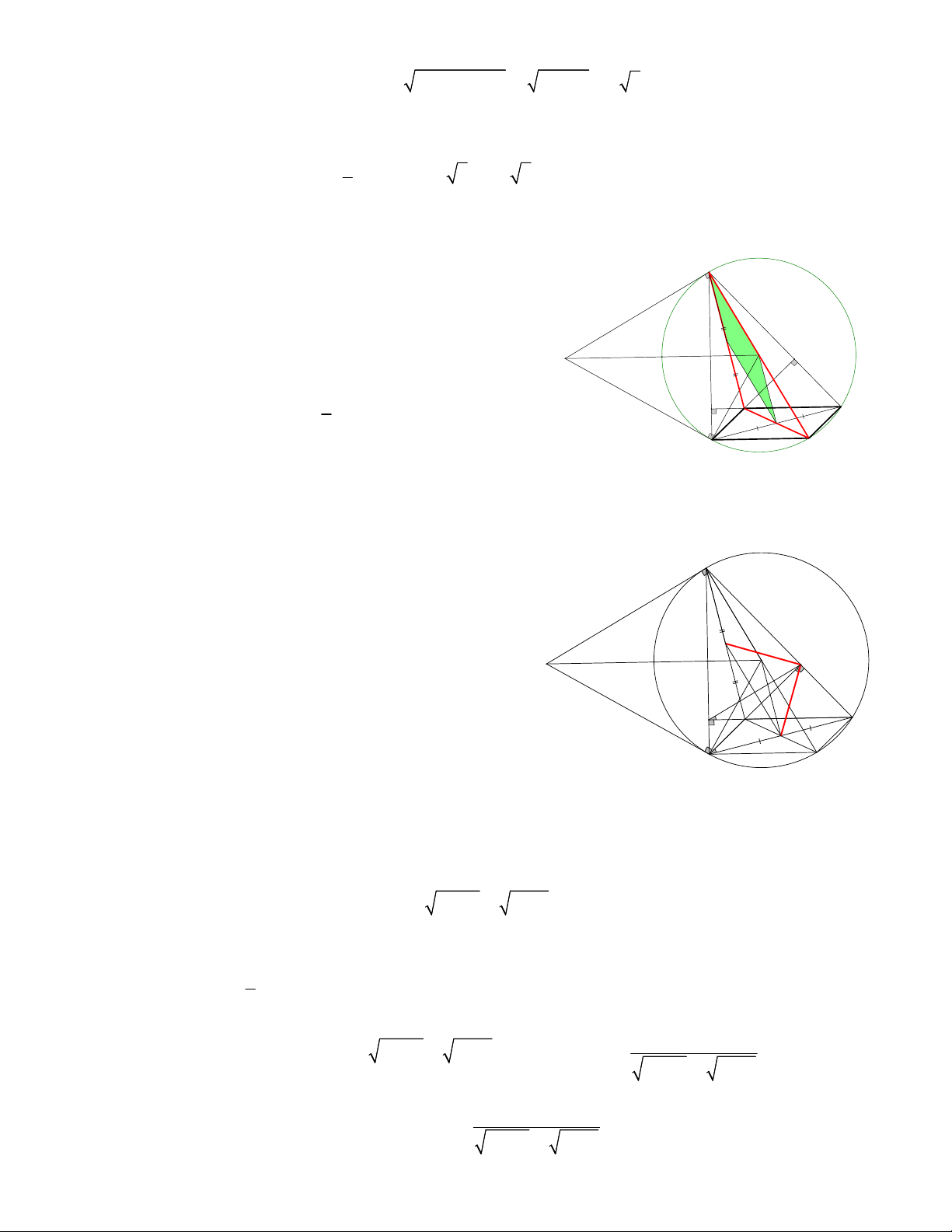
a) Chứng minh tứ giác MAOB nội tiếp. Tính diện tích S của tứ giác MAOB . A
 Xét tứ giác MAOB , có: 3 3 3   MAO MBO 90   M O 6
(Do MA, MB lần lượt là tiếp tuyến của đường tròn O).   MAO MBO 90 90 180      B Mà hai góc  
MAO, MBO ở vị trí đối nhau, nên tứ giác MAOB nội tiếp.
 Áp dụng định lý Pytago vào tam giác MAO vuông tại A MA  MO2  AO2 2 2  6  3  3 3. Dễ thấy MAO  M  BO c  c  c  S  S 1 2.     2. M . AA . O 3 3.3 9 3 . MAOB MAO 2 b) Lấy điểm C...
 Chứng minh tứ giác AJNO là hình bình hành A
Kẻ đường kính AD. Ta c/m được tứ giác BHCD là hình bình hành.  N là trung điểm HD. J M O E
Xét tam giác AHD có ON là đường trung bình, nên: 1 F
ON // AH và ON  AH Hay ON // AJ và C 2 H N ON  AJ B D
Vậy tứ giác AJNO là hình bình hành.  Chứng minh  JEN 90  A
Ta có EN là trung tuyến của tam giác vuông BEC    BEN  EBN Tứ giác BCEF nội tiếp    EBN  EFC J M E O Tứ giác AFHE nội tiếp    EFC  EAH F C Mà  
EAH  JEA (do JE là trung tuyến tam giác H vuông AEH) N B D Do đó   BEN  AEJ       JEN JEB BEN JEB AEJ BEA 90        . Câu 5. (0,5 điểm) x  y  y2  y  y 2  1  x  y
Giải hệ phương trình  . x y 3  x 4 y2  x 7 y  x 5  y  19   0  1
Điều kiện: y  ;x  y  0 . 2 y 2  1  x  y
Xét phương trình: xy  y2  y  y
2  1  x  y  y x  y  1    y 2  1  x  y     x  y  y 1 1    0  y 2 1 x y       y   x  1   y 1   0 *  y 2  1  x   y
Dễ thấy phương trình * vô nghiệm (do y 1   0 ) 2
Thế y  x  1 vào pt x y 3  xy2 4  x 7 y  x 5  y  19  0  x4  x3  x2 3  x
3  18  0  x  x  x2 3 2  x 2  3  0 x   3  y  4N    x   2  y  3  N 
Vậy hệ pt có nghiệm là x;y    2;3;3;4.