Đề tuyển sinh lớp 10 môn Toán năm 2025 – 2026 sở GD&ĐT Cao Bằng

ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ
ĐỀ TUYỂN SINH VÀO LỚP 10 CAO BẰNG
NĂM HỌC: 2025 – 2026 MÔN THI: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian phát đề) Câu 1. (4,0 điểm)
a) Thực hiện phép tính: 16 − 2 25 .
b) Tìm b để đồ thị hàm số y = 3x + b đi qua điểm M (2;8). c) Giải phương trình: 2
3x + x − 4 = 0 .
d) Giải hệ phương trình: 2x − y = 4 . 3   x + y =1 Câu 2. (1,5 điểm)
Một sân trường hình chữ nhật có chiều dài lớn hơn chiều rộng 16 m . Hai lần chiều dài nhỏ hơn năm
lần chiều rộng 100 m . Tính chiều dài và chiếu rộng của sân trường. Câu 3. (0,75 điểm)
Gieo đồng thời một con xúc xắc và một đồng xu. Hãy mô tả không gian mẫu của phép thử và tính
xác suất để số chấm xuất hiện trên con xúc sắc là số lẻ. Câu 4. (0,75 điểm)
Cho tam giác ABC vuông tại A có cạnh góc vuông AB = 4 cm ;  ACB = 30 . Tính  ABC và độ dài
các cạnh AC, BC . Câu 5. (2,0 điểm) Cho đường tròn ( ;
O R) và một điểm S nằm ngoài đường tròn. Từ điểm S kẻ hai tiếp tuyến , SA SB với đường tròn ( ; O R)( ,
A B là các tiếp điểm).
a) Chứng minh tứ giác OASB là tứ giảc nội tiếp.
b) Kẻ đường kính BD của đường tròn ( ;
O R) . Đường thẳng SD cắt đường tròn ( ;
O R) tại C(C khác
D) . Gọi I là giao điểm của SO và AB . Tia CI cắt đường tròn ( ;
O R) tại điểm thứ hai là M .
Chứng minh SCI đồng dạng với SOD và SO song song với BM . Câu 6. (1,0 điểm) Cho phương trình 2
x − mx − 3 = 0 (với m là tham số). Tìm m đề phương trình có hai nghiệm phân 2(x + x + 5 1 2 )
biệt x , x sao cho =
đạt giá trị lớn nhất. 1 2 H 2
x + mx − x x 2 1 1 2
---------- HẾT ---------- THCS.TOANMATH.com Trang 1
ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ
HƯỚNG DẢN GIẢI CHI TIẾT ĐỀ THI VÀO 10 NĂM HỌC 2025-2026 Câu
Ý Hướng dẫn giải của
a) Thực hiện phép tính: 16 − 2 25 . a) Cách giải: 2
16 − 2 25 =16 − 2 5 =16 − 2.5 =16 −10 = 6
b) Tìm b để đồ thị hàm số y = 3x + b đi qua điểm M (2;8). Cách giải: 8 = 3.2 + b
b) Thay x = 2;y =8 vào hàm số ta có 8 = 6 + b b = 2 Vậy b = 2 . c) Giải phưong trinh: 2
3x + x − 4 = 0 . Câu Cách giải: 1: (4 Ta có: 2 Δ =1 − 4.3.( 4 − ) =1+ 48 = 49 > 0 điểm)
Phương trình có hai nghiệm phân biệt: c) b − + Δ 1 − + 49 b − − Δ 1 − − 49 4 x 1; x − = = = = = = 1 2 2a 2.3 2a 2.3 3  x =1 1 S  = 4 − x = 2  3
d) Giải hệ phương trình: 2x − y = 4 3   x + y = 1. d) Cách giải:
Cộng vế với vế ta có: 5  x = 5 x =1 3    x + y = 1. 3  ⋅1+ y = 1. x =1  y = 2 −
Vậy hệ phương trình có nghiệm (x, y) = (1; 2 − ) . THCS.TOANMATH.com Trang 2
ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ
Một sân trường hình chữ nhật có chiều dài lớn hơn chiều rộng 16m. Hai lần chiều
dài nhỏ hơn năm lần chiều rộng 100 m . Tính chiều dài và chiều rộng của sân trường. Cách giải:
Gọi chiều rộng của sân trường hình chữ nhật là x(m)(ĐK : x > 0) .
Vì sân trường hình chữ nhật có chiều dài lớn hơn chiều rộng 16 m nên chiều dài Câu
của sân trường hình chữ nhật là x +16( m) 2:
Vi hai lần chiều dài nhỏ hơn năm lần chiều rộng 100 m nên ta có phương trình: (1,5
2(x +16) +100 = 5x điểm)
2x + 32 +100 = 5x 3x =132 x = 44(tm)
Suy ra, chiều rộng của sân trường là 44 m , chiều dài của sân trường là 44 +16 = 60( m).
Vậy chiều rộng của sân trường là 44 m , chiều dài của sân trường là 60 m .
Gieo đồng thời một con xúc sắc và một đồng xu. Hãy mô tả không gian mẫu của
phép thử và tính xác suất để số chẩm xuất hiện trong con xúc sắc là số lẻ. Cách giải:
Gọi 1;2;3;4;5;6 là kết quà gieo con xúc sắc xuất hiện mặt tương ứng 1 chấm, 2
chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm.
Gọi S là kết quả gieo đồng xu xuất hiện mặt sấp, N là kết quả gieo đồng xu xuất hiện mặt ngửa. Câu
Không gian mẫu cua phép thử Gieo đồng thời một con xúc sắc và một đồng xu 3: là: (0,75 Ω = (
{ 1;S);(1;N);(2;S);(2;N);(3;S);(3;N);(4;S);(4;N);(5;S);(5;N);(6;S);(6;N)} điểm)
Suy ra, số phần tử của không gian mẫu là n(Ω) =12.
Gọi A là biến cố: "số chấm xuất hiện trong con xúc sẳc là số lẻ". Ta có: A = (
{ 1;S);(1;N);(3;S);(3;N);(5;S);(5;N)}
Suy ra, số kết quả thuận lợi cho biến cố A là 6 nên n( A) = 6.
Vậy xác suất của biến cố A là: P( A) n( A) 6 1 = = = . n(Ω) 12 2 THCS.TOANMATH.com Trang 3
ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ
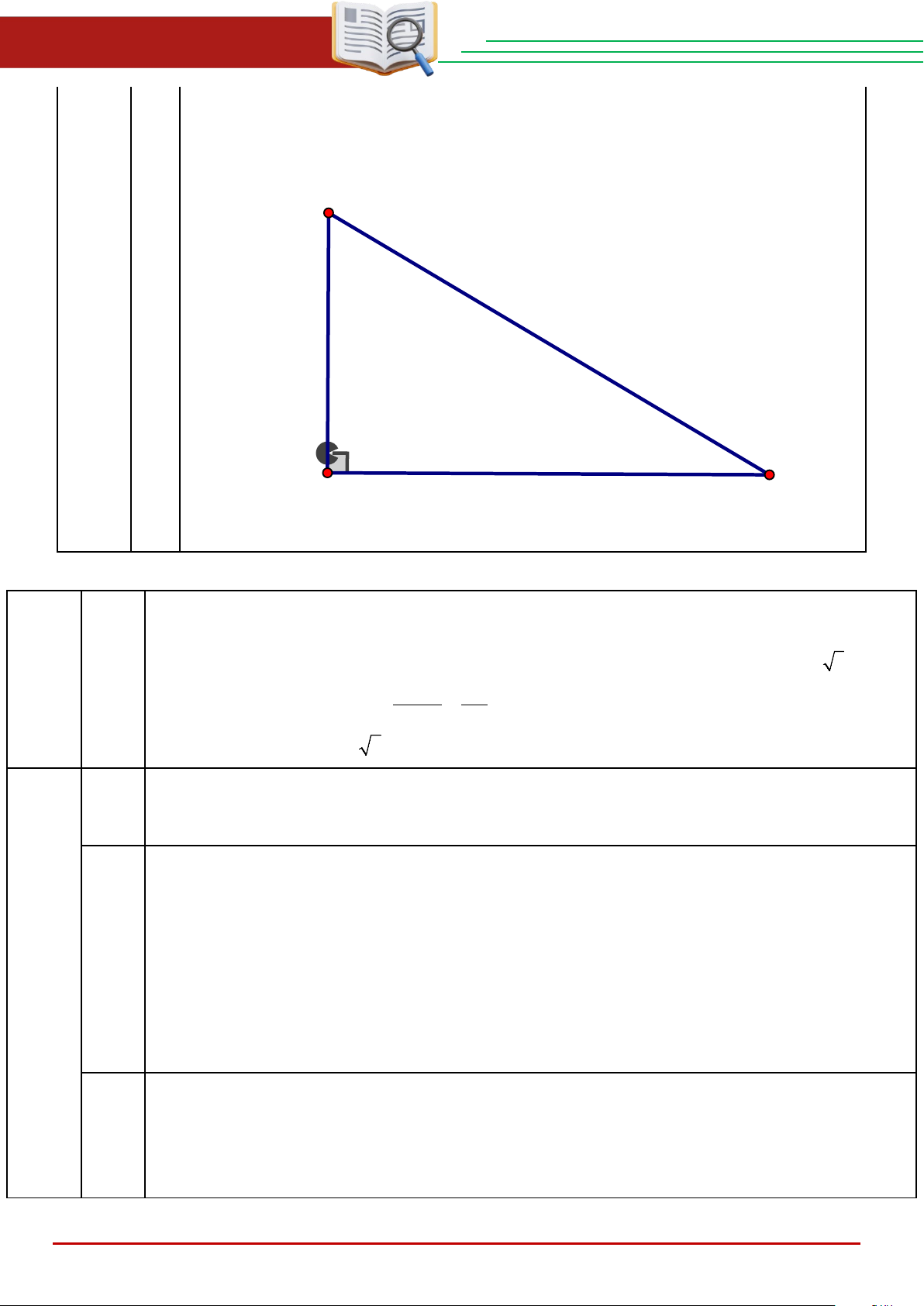
Cho tam giác ABC vuông tại A có cạnh góc vuông AB = 4 cm;∠ ACB = 30 .
Tính ∠ ABC và độ dài các cạnh AC, BC . B Câu 4: (0,75 điểm) 30° A C Cách giải:
Tam giác ABC vuông tại A nên ta có ∠ ABC + ∠ ACB = 90
Suy ra ∠ ABC = 90 −∠ ACB = 90 −30 = 60
Áp dụng hệ thức giữa góc và cạnh trong tam giác vuông ta có: AC = AB⋅cot30 = 4 3( cm) AB AB 4
= BC ⋅sin30 suy ra BC = = = 8( cm) sin30 0,5
Vậy ∠ ABC = 60; AC = 4 3 cm;BC = 8 cm Cho đırờng tròn ( ;
O R) và một điểm S nằm ngoài đırờng tròn. Từ điểm S kẻ hai tiếp tuyến
SA, SB với đường tròn ( ; O R)( ,
A B . là hai tiếp điểm).
a) Chứng minh tứ giác OASB là tứ giác nội tiếp Cách giải:
Ta có: SAO vuông tại A (do SA là tiếp tuyến của (O) ) Do đó S, ,
A O cùng thuộc đường tròn đường kính SO (1) Câu a) 5: (2
SBO vuông tại B (do SB là tiếp tuyến của (O) ) điểm)
Do đó S, B,O cùng thuộc đường tròn đường kính SO (2)
Từ (1) và (2) suy ra S, ,
A B,O cùng thuộc đường tròn đường kính SO
Vậy OASB là tứ giác nội tiếp
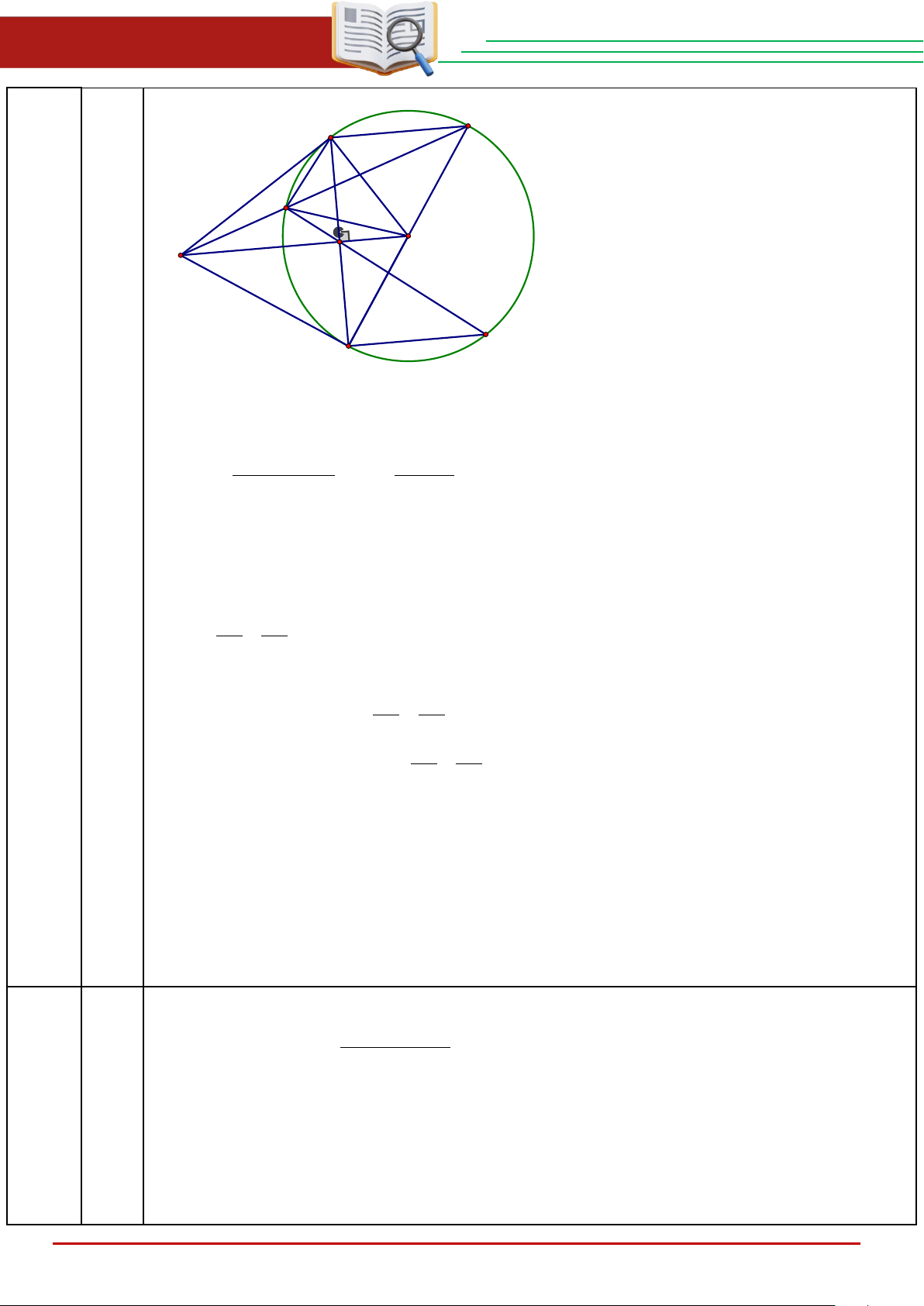
b) Kẻ đường kính BD của đường tròn ( O, R ). Đıròng thẳng SD cắt đường tròn (O, R) tại b)
C( C khác D) . Gọi I là giao điểm của SO và AB . Tia CI cắt đường tròn (O, R) tại điểm thứ hai là M.
Chứng minh SCI đồng dạng với SOD và SO song song với BM THCS.TOANMATH.com Trang 4
ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ D A C O S I M B Cách giải:
b) Ta có: ∠ SAC + ∠ OAC = ∠ SAO = 90 nên ∠ SAC = 90 −∠ OAC (3)
Tam giác OAC cân tại O( do OA = OC) nên 180 − ∠ AOC ∠ ∠ = = 90 AOC OAC −
= 90 − ∠ ADC (4) 2 2
Từ (3) và (4) ta có ∠ SAC = ∠ SDA
Xét SAC và SDA có
LDSA chung ∠ SAC = ∠ SDA(cmt)
Do đó SAC ∼SDA(g.g) Suy ra SA SD = hay 2
SA = SC.SD SC SA
Ta chứng minh được SAI ∼SOA(g.g) suy ra 2
SA = SI.SO
Do đó SC.SD = SI.SO hay SC SI = SO SD SC SI Xét =
SCI và SOD có SO SD ∠ DSO chung
Do đó SCI ∼SOD( c.g.c )
Suy ra ∠ SIC = ∠ SDO
Mà ∠ SDO = ∠ CMB (cùng chắn cung BC )
Nên ∠ SIC = ∠ CMB
Hơn nữa hai góc này ở vị tri đồng vị nên SI B ‖ M Vậy SO B ‖ M Cho phương trình 2
x − mx − 3 = 0 (với m là tham số). Tìm m để phương trình có hai nghiệm 2(x + x + 5 1 2 )
phân biệt sao cho H =
đạt giá trị lớn nhất 2
x + mx − x x 2 1 1 2 Câu Cách giải: 6: (1 Ta có: 2 = −m − (− ) 2
Δ ( ) 4. 3 = m +12 > 0, m ∀ ∈  điểm)
Do đó phương trình đã cho luôn có 2 nghiệm phân biệt x , x 1 2
Theo định li Viete ta có x + x = m 1 2  x x = 3 −  1 2 THCS.TOANMATH.com Trang 5
ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ
Vì x là nghiệm của phương trình đã cho nên 2
x − mx − 3 = 0 hay 2 x = mx + 3 2 2 2 2 2 2(x + x + 5 2 x + x + 5 1 2 ) ( 1 2) Khi đó 2m + 5 H = = =
mx + 3+ mx − x x m(x + x ) 2 + 3− x x m + 6 2 1 1 2 1 2 1 2 2 2 2 2m + 5
2m + 5 − m − 6 −m + 2m −1 −(m −1) Ta có: H −1= −1 = = = 2 2 2 2 m + 6 m + 6 m + 6 m + 6 2 Vi 2 2
−(m −1) ≤ 0,m + 6 > 0, m
∀ ∈  nên −(m −1) ≤ 0 hay H ≤1 2 m + 6
Dấu " = " xày ra khi và chi khi m =1 Vậy m =1 THCS.TOANMATH.com Trang 6