Đề tuyển sinh lớp 10 môn Toán năm 2025 – 2026 sở GD&ĐT Thái Bình

ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN TOÁN (Chung) Câu Ý Nội dung Điểm Câu 1 a)
2,0 đ 0,5 Với x = 9 thỏa mãn ĐKXĐ thay vào B ta được 9 9 4 B − + = 0,25 9 − 4 9 3 4 B − + = = 10 − . Vậy B = 10 − tại x = 9 . 0,25 3 − 4 b) 6 x −8 x 2 1,0 A = + + 0,25
( x + 4)( x − 4) x + 4 x − 4
6 x −8 + x( x − 4) + 2( x + 4) A = 0,25
( x + 4)( x − 4)
6 x −8 + x − 4 x + 2 x + 8 x + 4 x A = = 0,25
( x + 4)( x − 4)
( x + 4)( x − 4) x( x + 4) x A = = . Vậy = x A
với x ≥ 0, x ≠ 16. 0,25
( x + 4)( x − 4) x − 4 x − 4 c) A x x − x + x
0,5 Với x ≥ 0, x ≠ 16 thì B ≠ 0 nên 4 P = = : = 0,25 B x − 4 x − 4 x − x + 4
+ Xét với x = 0 (thỏa mãn ĐKXĐ) ta có P = 0 .
+ Xét với x > 0, x ≠ 16 , ta có x x x x 1 P = = = ≤ = 2
x − x + 4 x − 4 x + 4 + 3 x ( x − 2) + 3 x 3 x 3 0,25
Dấu “=” xảy ra khi x = 4 (thỏa mãn ĐKXĐ) Vậy 1
max P = khi x = 4 . 3 Câu 2 a)
Bảng tần số tương đối:
2,5 đ 0,75 Số bài tập đã làm 6 7 8 9 10
Tần số tương đối (%) 20 25 30 15 10
Đúng từ 1 đến 2 ý: 0,25 0,75
Đúng từ 2 đến 3 ý: 0,5 Đúng 5 ý: 0,75 b)
Không gian mẫu Ω = {1;2;3;4;5;6;7;8;9;10;11;1 } 2 0,75 0,25
Số phần tử của Ω là n(Ω) =12
Các kết quả thuận lợi cho biến cố A là 3; 6; 9; 12
Số kết quả thuận lợi cho biến cố A là n( ) A = 4 0,25
Xác suất của biến cố A là n( ) A 4 1 P( ) A = = = n( 0,25 Ω) 12 3 c) 4 4
1,0 Thể tích của viên bi sắt là 3 3 V = r π = .3 π 0,25 3 3 3 V = 36 ( π cm ) 0,25
Theo bài ra thể tích nước dâng lên bằng thể tích viên bi sắt nên ta có: 2 R π x = 36π 0,25 THCS.TOANMATH.com Trang 3
ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ π( )2 3 2 .x = 36π 0,25 Suy ra 36 x π = = 2(cm) 18π Câu 3 a)
Gọi số cuốn sách ở ngăn I lúc đầu là x cuốn ( x ∈ , x >100)
2,0 đ 1,0 Số cuốn sách ở ngăn II lúc đầu là y cuốn ( y ∈, y > 0)
Số cuốn sách ở ngăn I nhiều hơn số cuốn sách ở ngăn II là 100 cuốn 0,25
Suy ra x − y =100 (1)
Chuyển 25% số cuốn sách ở ngăn I sang ngăn II thì số cuốn sách ở ngăn I
bằng 75% số cuốn sách ở ngăn II. Ta có: 75 75  25 x  y x = + 100 100 100    0,25 1
x = y + x 4 3 y = x (2) 4
Từ (1) và (2) ta có hệ phương trình: x − y = 100   3 y =  x  4 0,25  =
Giải hệ phương trình ta được x 400  (thỏa mãn ĐK)  y = 300
Vậy số cuốn sạc ở ngăn I lúc đầu là 400 cuốn
Số cuốn sách ở ngăn II lúc đầu là 300 cuốn. 0,25 b)
Từ giả thiết suy ra A(3; 8 − ) 0,25 1,0 Suy ra 2 8 − = .3 a 8 a − = 3 0,25 Phương trình parabol là 8 2 y = − x 9
MN = 3 suy ra hoành độ của điểm M là 3 x = M 2 2 0,25 Suy ra 8 3 y   = − = − M .  2 9  2 
Khoảng cách từ dây đèn đến mặt sân bằng: y − y = − + = m M A 2 8 6( ) 0,25 THCS.TOANMATH.com Trang 4
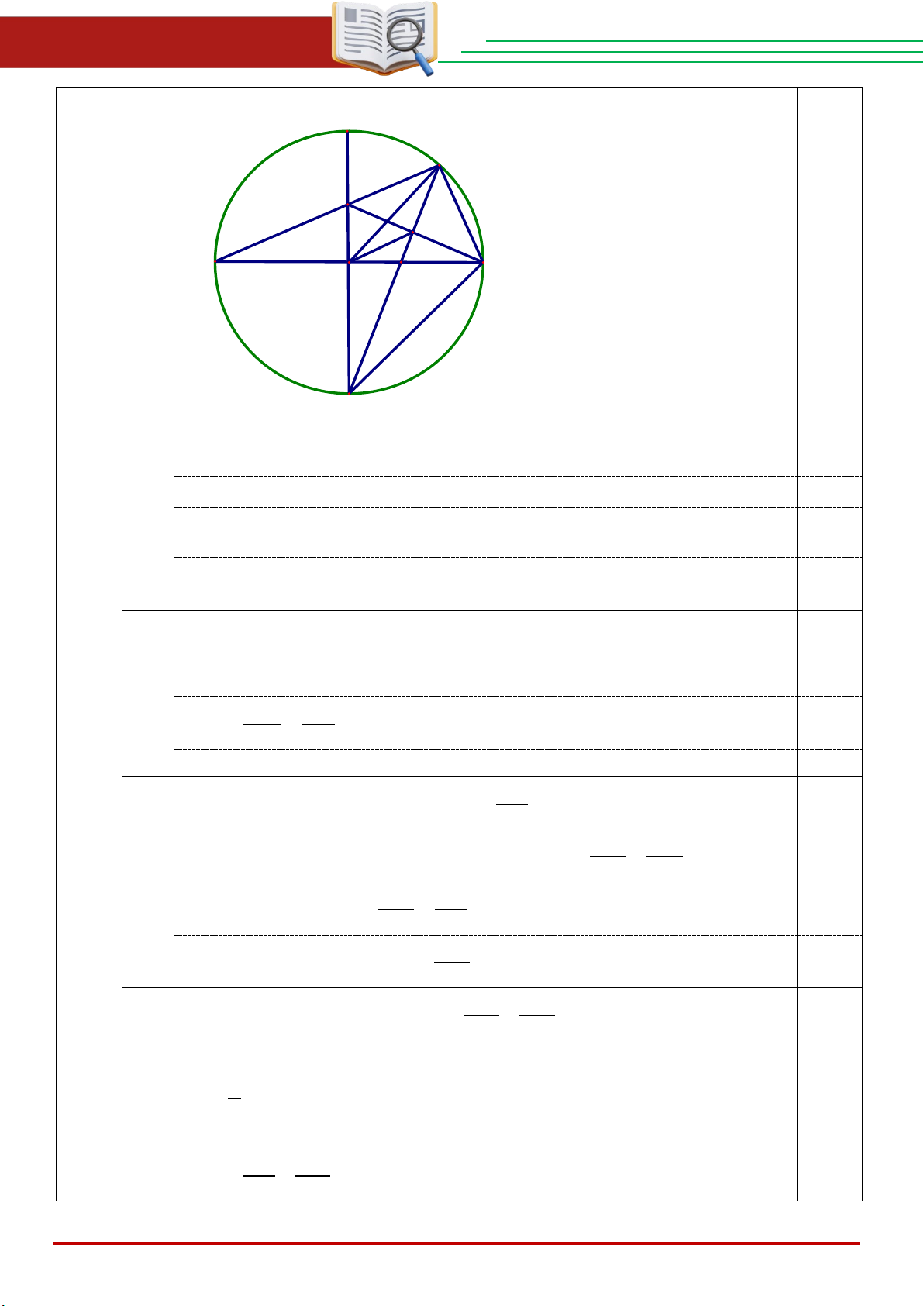
ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ Câu 4 3,0 đ C M K E A B O I D a)
Vì AB ⊥ CD tại O nên BOK ∆ vuông tại O 1,0 Do đó BOK ∆
nội tiếp đường tròn đường kính BK (1) 0,25 Lại có 
AMB = 90° (góc nội tiếp chắn nửa đường tròn) 0,25 Suy ra B
∆ MK vuông tại M Nên B
∆ MK nội tiếp đường tròn đường kính BK (2) 0,25
Từ (1) và (2) suy ra 4 điểm O, B,M , K cùng thuộc đường tròn đường kính 0,25
BK . Do đó tứ giác OBMK nội tiếp. b) Ta có 
CMD = 90° (góc nội tiếp chắn nửa đường tròn) 0,75 Xét ODI ∆ và MD ∆ C có:  = 
DOI DMC = 90° , D chung 0,25 Suy ra ODI ∆ ∽ M ∆ DC (g.g) Suy ra DO DI = 0,25 DM DC Nên 2 DM.DI = . DO DC = .2 R R = 2R 0,25 c) 0,75 Xét ODI ∆ vuông tại O có  tan OI ODI = (3) 0,25 OD
Có OE là đường phân giác trong của O ∆ IM nên EI OI = EM OM 0,25
Mà OM = OD = R nên EI OI = (4) EM OD Từ (3) và (4) suy ra  tan EI ODI = 0,25 EM d) 0,5 Do ODI ∆ ∽ M
∆ DC (cmt) suy ra OI OD = MC MD Xét DBI ∆ và D ∆ MB có  BDM chung,  = 
IBD BMD = 45° (Góc nội tiếp chắn 1 đường tròn) 0,25 4 Nên DBI ∆ ∽ DM ∆ B (g.g) Suy ra IB DB = MB MD THCS.TOANMATH.com Trang 5
ĐỀ TUYỂN SINH VÀO 10 – 2025 – 2026 ĐẠI TRÀ Xét ODB ∆ có 
BOD = 90° và OB = OD = R nên ODB ∆ vuông cân tại O
. Suy ra DB = OD 2 Suy ra IB DB OD 2 = = . Mà OI OD = nên IB OI 2 = MB MD MD MC MD MB MC Suy ra MB IB 2.OI = = = 2 0,25 MC OI 2 OI 2 Câu 5 Ta có 0,5 đ 2 2 2 2 (b − c) (b + c) (3 − a) (a + 3) a + 3 6a + = 6a + − 2bc ≤ 6a + = = 2 2 2 2 2 0,25 2 2 Tương tự (c a) b 3 6b − + + ≤ và (a b) c 3 6c − + + ≤ 2 2 2 2
Cộng vế với vế của 3 bất đẳng thức trên ta được: 2 2 2 (b − c) (c − a) (a − b)
a + b + c + 9 6a + + 6b + + 6c + ≤ = 6 2 2 2 2 2  + + =
Dấu “=” xảy ra khi a b c 3  0,25
ab = bc = ca = 0  = =  = =  = = Hay a b 0 b c c a  hoặc 0  hoặc 0  c = 3 a = 3 b  = 3 THCS.TOANMATH.com Trang 6
Document Outline

• de-tuyen-sinh-lop-10-mon-toan-nam-2025-2026-so-gddt-thai-binh
  • de Doc1
• THÁI BÌNH - TS 10 25 26 - NGUYỄN HỒNG - 0386536670 - CĐGVTOÁNVN