Đề tuyển sinh lớp 10 THPT môn Toán năm 2018 – 2019 sở GD và ĐT Bình Dương

SỞ GIÁO DỤC & ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT BÌNH DƯƠNG
Năm học: 2018 – 2019 ĐỀ CHÍNH THỨC Môn thi : TOÁN
Thời gian: 120 phút (không kể thời gian giao đề) Bài 1 (1,5 điểm)
1) Rút gọn biểu thức: A = ( − )2 5 2 + 40 ; ⎛ x − x x +1 ⎞ x + 1
2) Rút gọn biểu thức: B = ⎜ − ⎟ :
vôùi x > 0, x ≠ 1. x −1 x + x x ⎝ ⎠
Tính giá trị của B khi x = 12 + 8 2 Bài 2 (1,5 điểm) Cho parabol (P): 2
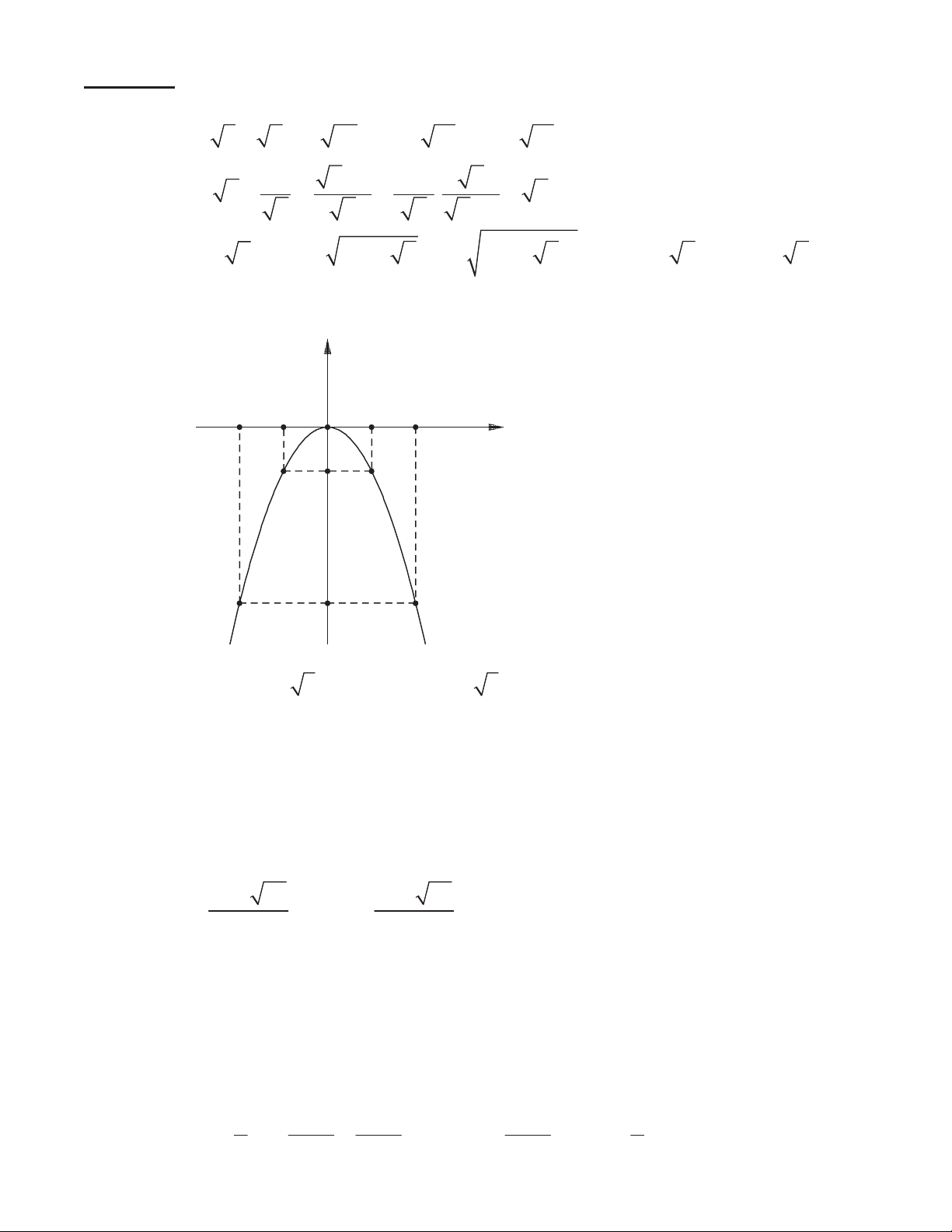
y = −x và đường thẳng (d): y = 2 3x + m + 1 (m laø tham soá) . 1) Vẽ đồ thị (P).
2) Tìm tất cả các giá trị của tham số m để (d) cắt (P) tại hai điểm phân biệt. Bài 3 (2 điểm) ⎧9x + y =11
1) Giải hệ phương trình ⎨ ⎩5x + 2y = 9 2) Cho phương trình 2 2
x − 2(m + 2)x + m + 3m − 2 = 0 (1) , ( m là tham số).
a) Giải phương trình (1) với m = 3 ;
b) Tìm các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt
x , x sao cho biểu thức 2 2
A = 2018 + 3x x − x − x đạt giá trị nhỏ nhất. 1 2 1 2 1 2 Bài 4 (1,5 điểm)
Một người dự định đi xe máy từ tỉnh A đến tỉnh B cách nhau 90km trong một thời
gian đã định. Sau khi đi được 1 giờ người đó nghỉ 9 phút. Do đó, để đến tỉnh B đúng
hẹn, người ấy phải tăng vận tốc thêm 4km/h. Tính vận tốc lúc đầu của người đó. Bài 5 (3,5 điểm)
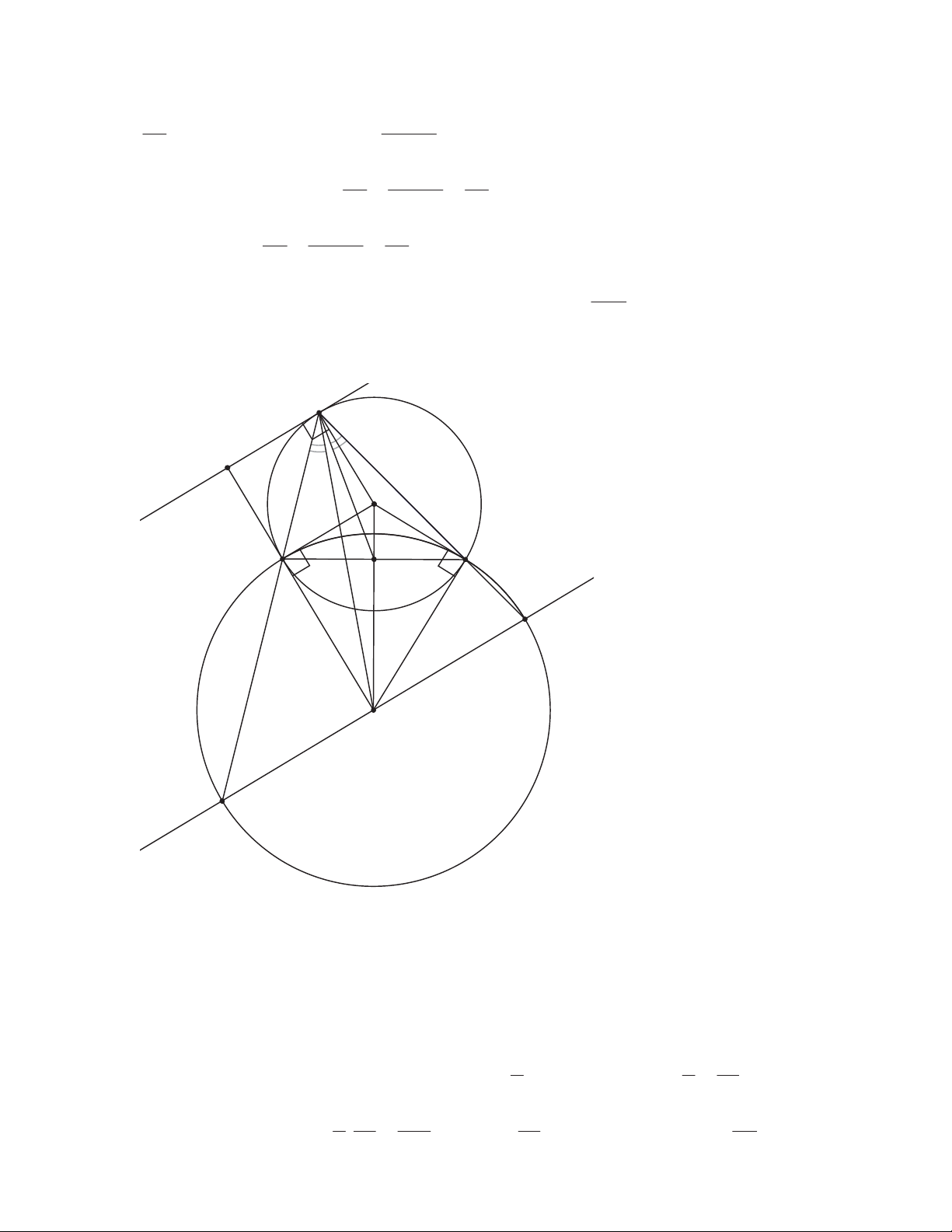
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) có bán kính R= 3cm. Các
tiếp tuyến với (O) tại B và C cắt nhau tại D.
1) Chứng minh tứ giác OBDC nội tiếp đường tròn.
2) Gọi M là giao điểm của BC và OD. Biết OD = 5cm. Tính diện tích tam giác BCD.
3) Kẻ đường thẳng d đi qua D và song song với đường tiếp tuyến với (O) tại A, d cắt
các đường thẳng AB, AC lần lượt tại P, Q. Chứng minh: AB.AP = AQ.AC
4) Chứng minh: góc PAD bằng góc MAC. …………Hết……….. ĐÁP ÁN: Bài 1: 1) A = ( − )2 5
2 + 40 = 5 − 2 10 + 2 + 2 10 = 7 ; ⎛ 1 ⎞ x + 1 x −1 2) = − : = . x B x = x −1 ⎜ ⎟ ⎝ x ⎠ x x x + 1
x = 12 + 8 2 ⇒ B = + − = ( + )2 12 8 2 1 2 2 2 −1 = 2 + 2 2 −1 =1+ 2 2 Bài 2:
1) parabol (P) qua 5 điểm (0;0), (1;− ) 1 , ( 1 − ;− ) 1 , (2; 4 − ), ( 2 − ; 4 − ) y O x -2 -1 1 2 -1 -4
2) (d) cắt (P) tại hai điểm phân biệt khi phương trình hoàng độ giao điểm của hai đường là 2 2
−x = 2 3x + m +1 ⇔ x + 2 3x + m +1 = 0 có 2 nghiệm phân biệt ⇔
Δ =12 − 4m − 4 > 0 ⇔ m < 2 . Bài 3: ⎧9x + y =11 ⎧y =11− 9x ⎧ y =11− 9x ⎧x =1 1) ⎨ ⇔ ⎨ ⇔ ⎨ ⇔ ⎨ ⎩5x + 2y = 9 5
⎩ x + 22 −18x = 9 ⎩x =1 ⎩ y = 2 2) 2 2
x − 2(m + 2)x + m + 3m − 2 = 0 (1) a) 2
m = 3 ⇒ x −10x + 16 = 0 có Δ = 36 > 0 nên có 2 nghiệm phân biệt 10 + 36 10 − 36 x = = 8, x = = 2 1 2 2 2
b) Điều kiện (1) có 2 nghiệm phân biệt là 2 2
Δ = 4(m + 4m + 4) − 4(m + 3m − 2) > 0 ⇔ m > −6 (*)
⎧x + x = 2(m + 2) Theo Viét, ta có: 1 2 ⎨ 2
x x = m + 3m − 2 ⎩ 1 2 2 2 2 2
A = 2018 + 3x x − x − x = 2018 + 5x x − (x + x ) = m − m + 1992 1 2 1 2 1 2 1 2 2 ⎛ 1 ⎞ 7969 7969 7969 1 = m − + ≥ ⇒ min A = khi m = ⎜ ⎟ thoûa (*) ⎝ 2 ⎠ 4 4 4 2 Bài 4:
Gọi x(km/h) là vận tốc đi lúc đầu (x > 0), x + 4 là vận tốc đi lúc sau. 90 90 −
là thời gian đi dự định,
x là thời gian đi lúc tăng vận tốc. x x + 4 9 90 − x 90 Ta có phương trình 1+ + = 60 x + 4 x 23 90 − x 90 Phương trình + = trở thành 2
3x + 92x − 7200 = 0 20 x + 4 x 200
Có Δ = 94864 > 0 nên có hai nghiệm x = 36, = − 1 x2 3
Theo điều kiện, vận tốc lúc đầu của người đó là 36 km / h . Bài 5: A I x O B C M d Q D P 1)  o  0
OBD = 90 ,OCD = 90 (tính chất tiếp tuyến) ⇒   0
OBD + OCD = 180 ⇒ tứ giác OBDC nội tiếp.
2) OB = OC, DB = DC (tính chất hai tiếp tuyến cắt nhau) ⇒ OD là trung trực BC.
ΔOBD vuông tại B, đường cao BM ⇒ 9 9 16 2 2
OB = OM .OD ⇒ 3 = OM .5 ⇒ OM =
(cm) ⇒ MD = 5 − = (cm) 5 5 5 9 16 144 12 24 2
BM = OM .MD = . = ⇒ BM =
(cm) ⇒ BC = 2BM = (cm) 5 5 25 5 5 1 1 24 16 192 Diện tích ΔBCD là 2 S = BC.MD = . . = = 7,68(cm ) BCD 2 2 5 5 25
3) Gọi Ax là tia tiếp tuến của (O) tại A. d//Ax ⇒  
xAB = BPQ (so le) 1 mà    xAB = ACB = sñAB ⇒   ACB = BPQ (*) 2
⇒ ΔABC ∼ ΔAQP ⇒ AB AC = ⇒ A .
B AP = AC.AQ AQ AP
4) Gọi I là giao của hai tiếp tuyến tại A và tại B của (O) ⇒ IA = IB
ΔAIB ∼ ΔPDB (g,g,g) ⇒ DB = DP Tương tự ⇒ DC = DQ
Mà DB = DC ⇒ DP = DQ ⇒ D trung điểm PQ
ΔAQP ∼ ΔABC ⇒ AP QP PD = = AC BC CM ΔAPD và ΔACM có  
APD = ACM và AP PD = ⇒ ΔAPD ∼ ΔACM AC CM ⇒   PAD = MAC .
Gv: Lê Hành Pháp THPT Tân Bình − Bình Dương.