Đề tuyển sinh lớp 10 THPT môn Toán năm 2020 – 2021 sở GD&ĐT Cao Bằng

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT CAO BẰNG NĂM HỌC 2020-2021 ĐỀ CHÍNH THỨC Môn: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Câu 1. (4,0 điểm)
1) Thực hiện phép tính: 5 9 − 3 4
2) Tìm a để đồ thị hàm số y = ax + 5đi qua điểm M (3;− ) 1
3) Giải hệ phương trình: 2 2x − 3x +1= 0 4x + 5y = 3
4) Giải hệ phương trình:  x − 3y = 5 Câu 2. (2,0 điểm)
Bác An đi x ô tô từ Cao Bằng đến Hải Phòng. Sau khi đi được nửa quãng
đường, bác An cho xe tăng vận tốc thêm 5km / h nên thời gian đi nửa quãng đường
sau ít hơn thời gian đi nửa quãng đường đầu là 30phút. Hỏi lúc đầu bác An đi xe
với vận tốc bao nhiêu ? Biết rằng khoảng cách từ Cao Bằng đến Hải Phòng là 360k . m Câu 3. (1,0 điểm)
Cho tam giác ABC vuông tại .
A Biết AB = 6c , m AC = 8c . m
a) Tính độ dài cạnh BC
b) Kẻ đường cao AH.Tính độ dài đoạn AH Câu 4. (2.0 điểm)
Qua điểm Anằm ngoài đường tròn (O)vẽ hai tiếp tuyến ABvà AC của
đường tròn (B,C là các tiếp điểm)
a) Chứng minh ABOC là tứ giác nội tiếp
b) Kẻ đường thẳng qua diểm Acắt đường tròn (O)tại hai điểm E và F sao cho
E nằm giữa A và F. Chứng minh BE.CF = BF.CE Câu 5. (1,0 điểm)
Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức 1 A = 2 2 − 3 − x
-------------------- HẾT --------------------
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT Bài 1.
1) Ta có: 5 9 − 3 4 = 5.3 − 3.2 =15 − 6 = 9
2) Vì đồ thị hàm số y = ax + 5đi qua điểm M (3;− )
1 nên thay x = 3, y = 1 − vào
hàm số y = ax + 5ta được: 1 − = .3 a + 5 ⇔ 3a = 6 − ⇔ a = 2 − Vậy a = 2 − 3) Ta có: 2 2x − 3x +1= 0 x =1
Phương trình trên có dạng a + b + c = 0 nên có hai nghiệm  1 x =  2
Vậy phương trình đã cho có hai nghiệm 1 x =1;x = 2 4) Ta có: 4x + 5y = 3 4x + 5y = 3 17  y = 17 − y = 1 − x = 2  ⇔  ⇔  ⇔  ⇔ x − 3y = 5
4x −12y = 20 x = 3y + 5 x 3.  ( )1 5  = − + y = 1 −
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = (2;− ) 1 Bài 2.
Gọi vận tốc lúc đầu của bác An đi là x(km / h)(x > 0)
Nửa quãng đường đầu và nửa quãng đường sau đều dài : 360: 2 =180(km)
Thời gian bác An đi nửa quãng đường đầu là 180 (giờ) x
Trên nửa quãng đường sau, bác An đi với vận tốc là x + 5(km / h)
Thời gian bác An đi nửa quãng đường sau là 180 (giờ) x + 5
Vì thời gian đi nửa quãng đường sau ít hơn thời gian đi nửa quãng đường đầu là 30phút 1
= giờ nên ta có phương trình 2 180 180 1
180(x + 5) −180x 1
180x + 900 −180x 1 − = ⇔ = ⇔ = x x + 5 2 x(x + 5) 2 2 x + 5x 2 900 1 2 2 ⇔
= ⇔ x + 5x =1800 ⇔ x + 5x −1800 = 0 2 x + 5x 2 2 ∆ = 5 − 4.( 1800 − ) = 7225⇒ ∆ = 85  5 − − 85 x = = 4 − 5(ktm)  1
Nên phương trình có hai nghiệm 2  5 − +  85 x = = 40(tm) 2  2
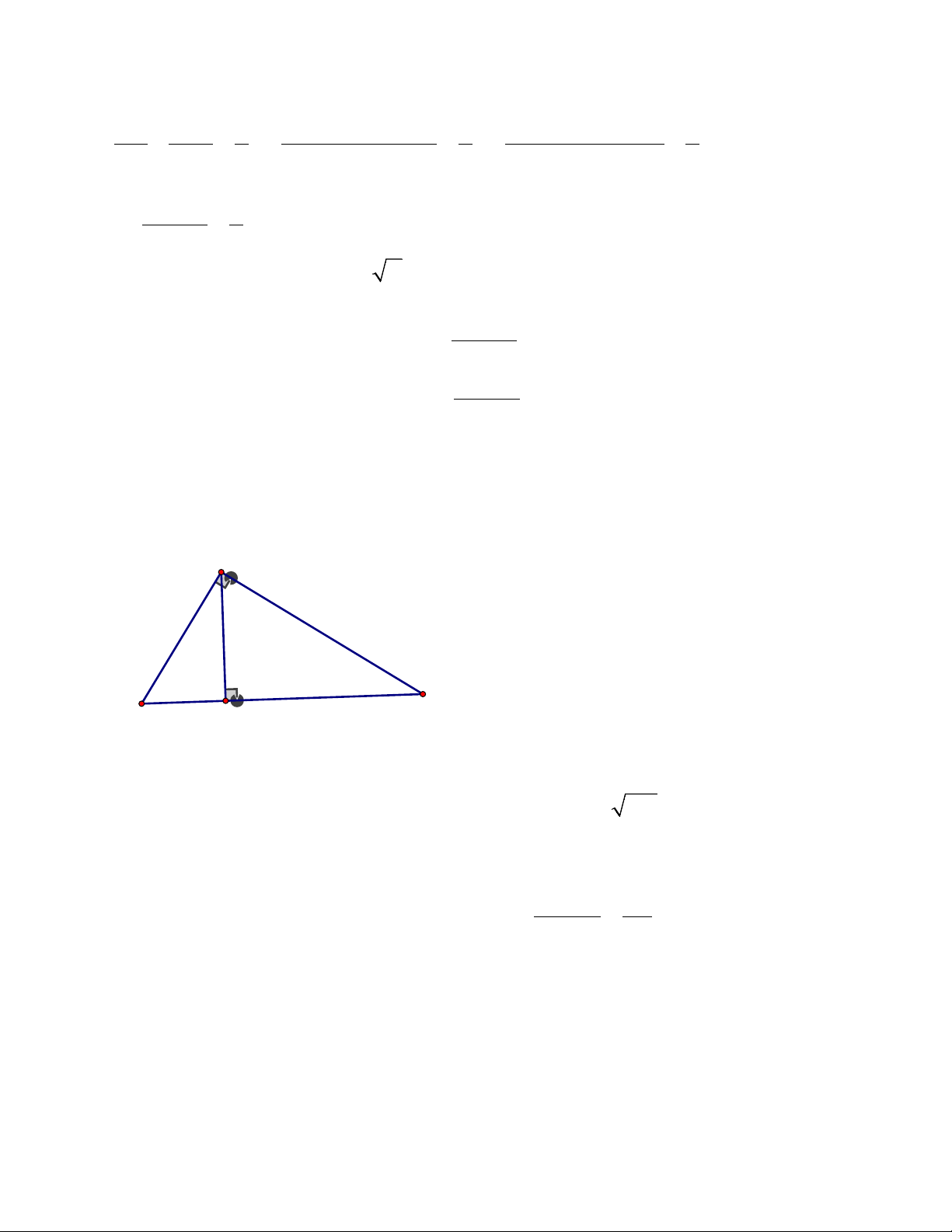
Vậy lúc đầu bác An đi với vận tốc 40km / h Bài 3. A B C H a) Xét A ∆ BC vuông tại ,
A theo định lý Pytago ta có: 2 2 2 2 2 2
BC = AB + AC ⇔ BC = 6 + 8 =100 ⇒ BC = 100 =10(cm) Vậy BC =10cm b) Xét A ∆ BC vuông tại ,
A có chiều cao AH, theo hệ thức lượng trong tam giác vuông, ta có : A . B AC 6.8
AH.BC = A . B AC ⇔ AH = = = 4,8(cm) BC 10
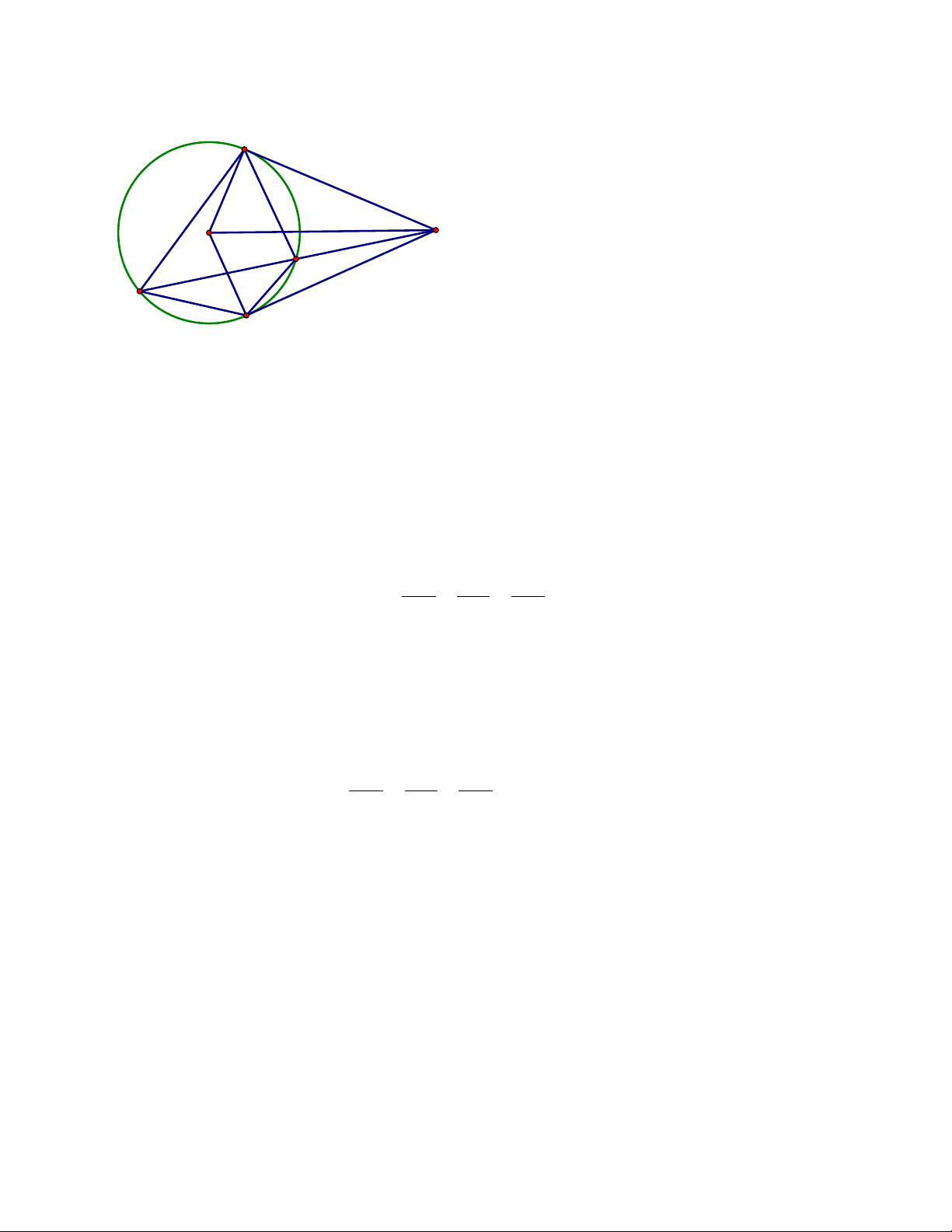
Vậy AH = 4,8cm Bài 4. B O A E F C
a) ABlà tiếp tuyến với (O)nên ⊥ ⇒  0 OB AB OBA = 90
AC là tiếp tuyến với (O)nên ⊥ ⇒  0 OC AC OCA = 90
Tứ giác ABOC có  +  0 0 0 OBA ACO = 90 + 90 =180
Do đó ABOC là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 ) b) Xét A ∆ BE và A
∆ FB có: Achung ;  = 
ABE AFC (cùng chắn cung BE) ⇒ ∆  ∆ ( . ) AB BE AE ABE AFB g g ⇒ = =
(các cặp cạnh tương ứng tỉ lệ) AF BF AF ⇒ A .
B BF = AF.BE và 2
AB = AE.AF Xét A ∆ CE và A ∆ FC có: Achung;  = 
ACE AFC (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn  CE) ⇒ ∆  ∆ ( . ) AC CE AE ACE AFC g g ⇒ = =
(các cặp cạnh tương ứng tỉ lệ) AF CF AC
⇒ AC.CE = AE.CF . Ta có: A .
B BF = AF.BE ;
AC.CE = AE.CF ⇒ A .
B BF.AC.CE = AF.BE.AE.CF 2
⇒ AB .BF.CE = AE.AF.BE.CF Mà 2
AB = AE.AF(cmt) ⇒ BF.CE = BE.CF(dfcm) Bài 5. 2 3  − x ≥  0 Điều kiện: 2  ⇔ x ≤ 3. Ta có: 2
2 − 3 − x ≠ 0 2 2 2
0 ≤ x ≤ 3 ⇒ 3 − 0 ≥ 3 − x ≥ 3 − 3 ⇒ 3 ≥ 3 − x ≥ 0 2 2
⇒ 3 ≥ 3 − x ≥ 0 ⇔ 2 − 3 ≤ 2 − 3 − x ≤ 2 1 1 1 ⇒ ≥ ≥ 2 2 − 3 2 − 3 − x 2 1 1 ⇒ ≤ A ≤ 2 2 − 3
Vậy GTNN của Alà 1 ⇔ x = 0;
GTLN của Alà 1 ⇔ x = ± 3 2 2 − 3
-------------------- HẾT --------------------
Document Outline

• Sở Cao Bằng