Đề tuyển sinh lớp 10 THPT môn Toán năm 2020 – 2021 sở GD&ĐT Hà Nam

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT HÀ NAM NĂM HỌC 2020 - 2021 MÔN THI: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
Câu 1 (2,0 điểm). 1) Giải phương trình 2
x  2x  3  0  
3 x  3y  5 2x  y
2) Giải hệ phương trình 
x2y   3
Câu 2 (2,0 điểm).
1) Rút gọn biểu thức A  2 3  27  42 3   2) Cho biểu thức  x x       : x B
1 (với x0, x 1).
 x 1 x  x  x1 Rút gọn biểu thức .
B Tìm tất cả các giá trị của x để biểu thức B nhận giá trị âm.
Câu 3 (1,5 điểm).
Trong mặt phẳng tọa độ Oxy, cho parabol P có phương trình y  x2 2 và đường
thẳng d có phương trình y  2x  m ( m là tham số).
1) Tìm m để đường thẳng ( d ) đi qua điểm M  ; 2 3.
2) Tìm điều kiện của m để parabol P cắt đường thẳng d tại hai điểm phân biệt. Gọi Ax Bx
là hai giao điểm của parabol P và đường thẳng d, xác định 2 ; y2  1; y1 ,
m để 1 x 2 16
1x2 2   y  1 y2 .
Câu 4 (4,0 điểm).
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn ( ;
O R). Hai đường cao
BE, CF của tam giác ABC cắt nhau tại H. Đường thẳng AH cắt BC tại D và cắt đường tròn ( ;
O R) tại điểm thứ hai là M.
1) Chứng minh tứ giác AEHF nội tiếp.
2) Chứng minh BC là tia phân giác của  EBM.
3) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF. Chứng minh IE là tiếp tuyến
của đường tròn ngoại tiếp tam giác BCE.
4) Khi hai điểm B, C cố định và điểm A di động trên đường tròn ( ; O R) nhưng vẫn
thỏa mãn điều kiện tam giác ABC có ba góc nhọn. Chứng minh OA  EF. Xác định vị trí
của điểm A để tổng DE  EF  FD đạt giá trị lớn nhất.
Câu 5 (0,5 điểm).
Cho ba số dương a, b, c thỏa mãn abc  1. Chứng minh rằng 1 1 1 1    a 2 b  3 b 2 c  3 c 2 a  3 2 ------HẾT------
Họ và tên thí sinh: ......................................................... Số báo danh: ............................. .....
Cán bộ coi thi thứ nhất: ................................... Cán bộ coi thi thứ hai: ........................... .....
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT HÀ NAM
NĂM HỌC 2020 – 2021
HƯỚNG DẪN CHẤM MÔN TOÁN
Lưu ý: - Các cách giải khác đáp án vẫn đúng cho điểm tương ứng theo biểu điểm
- Tổng điểm toàn bài không làm tròn. Câu Ý Nội dung Điểm 1) Giải phương trình 2
x − 2x − 3 = 0. 1.
Phương trình đã cho có a − b + c = 0 0,5
(1,0đ) Suy ra phương trình có hai nghiệm x = 1 − và x = 3. 0,5  
3 x  3y  5 2x  y
2) Giải hệ phương trình  .
x2y   3 3
 x + 9y +15 = 2x + y x + 8y = 15 − Câu 1 ⇔  ⇔  0,25 (2,0đ) x + 2y = 3 − x + 2y = 3 − 2. x + 8y = 15 − (1,0đ) ⇔  0,25 6y = 12 − x + 8y = 15 − ⇔  0,25 y = 2 − x −16 = 15 − x =1 ⇔  ⇔ 
Vậy hệ phương trình có nghiệm (1; 2 − ). 0,25 y = 2 − y = 2 −
1) Rút gọn biểu thức A = 2 3 − 27 + 4 − 2 3. 1. (1,0đ) A = − + ( − )2 2 3 3 3 3 1 0,5 = 2 3 − 3 3 + 3 −1 = 1 − 0,5   2) Cho biểu thức x x x −1 B =  −  : 
(với x > 0 , x ≠ 1). x +1 x +  x  x −1  Rút gọn biểu thức .
B Tìm tất cả các giá trị của x để biểu thức B nhận giá trị âm. Câu 2   −   − (2,0đ) x x x 1 B   = − x 1 x 1 =  −  :  x +1 x ( x +  x +1 x +  1 x −1  ) : 1  x −1  2.  0,25 (1,0đ) x 1 x  1  : x 1 x1 1 ( x − ) 1 ( x x + − )1 = . = x −1. 0,25 x +1 x −1
B < 0 ⇔ x −1< 0 ⇔ x <1⇒ x <1. 0,25
Kết hợp điều kiện, ta có 0  x 1. 0,25
Trong mặt phẳng tọa độ Oxy , cho parabol (P) có phương trình 2 y = 2x và
đường thẳng (d ) có phương trình y = 2x + m ( m là tham số). Câu 3 1. (1,5đ) (0,5đ)
1) Tìm m để đường thẳng ( d ) đi qua điểm M ( 2; − 3).
Vì đường thẳng (d ) đi qua điểm M ( 2; − 3) suy ra 3 = 2.( 2 − ) + m 0,25 Trang 1/4 ⇔ 3 = 4
− + m ⇔ m = 7. 0,25
2) Tìm điều kiện của m để parabol (P) cắt đường thẳng (d ) tại hai điểm
phân biệt. Gọi A(x ; y , B(x ; y là hai giao điểm của parabol (P) và 2 2 ) 1 1 )
đường thẳng (d ), xác định m để (1− x x )2 + 2 y + y =16. 1 2 ( 1 2)
Phương trình hoành độ giao điểm của (P) và (d ) là: 0,25 2 2
2x = 2x + m ⇔ 2x − 2x − m = 0 ( ) 1
Parabol (P) cắt đường thẳng (d ) tại hai điểm phân biệt ⇔ phương trình ( )
1 có hai nghiệm phân biệt ⇔ ∆′ > 0 . 0,25 ∆′ = 1+ 2m , 1
∆′ > 0 ⇔ 1+ 2m > 0 ⇔ m > − (*) . 2. 2 (1,0đ) x + x =1 1 2
Khi đó theo định lý Vi-et ta có  . . m x x = −  1 2  2
(1− x x )2 + 2 y + y =16 ⇔ (1− x x )2 + 2 2x + m + 2x + m =16 1 2 ( 1 2 ) 1 2 ( 1 2) 0,25 2
⇔ (1− x x )2 + 4 x + x + 4m =16 1 m  ⇔ + + 4 + 4m =   16 1 2 ( 1 2)  2  2 2 ⇔ 1 m + m + + 4 + 4m =16 m 2 ⇔
+ 5m + 5 =16 ⇔ m + 20m − 44 = 0 . 4 4 m = 2 ⇔ 
. Đối chiếu điều kiện (*) , ta có m = 2 . 0,25 m = 22 −
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn O R Hai đường ( ; ).
cao BE, CF của tam giác ABC cắt nhau tại H. Đường thẳng AH cắt BC
tại D và cắt đường tròn ( ;
O R) tại điểm thứ hai là M.
1) Chứng minh tứ giác AEHF nội tiếp. Câu 4 (4,0đ) 1. (1,0đ)
(Học sinh không vẽ hình ý nào sẽ không được chấm điểm ý đó) Ta có  o
AEH = 90 (vì BE là đường cao). 0,25 Ta có  o
AFH = 90 (vì CF là đường cao). 0,25 Trang 2/4 Suy ra  +  o AEH AFH =180 . 0,25
Vậy tứ giác AEHF nội tiếp (tứ giác có tổng 2 góc đối bằng o 180 ). 0,25
2) Chứng minh BC là tia phân giác của  EBM . Ta có  = 
MAC MBC (2 góc nội tiếp cùng chắn một cung) 0,25 2.
Vì H là trực tâm A
∆ BC ⇒ AD ⊥ BC . (1,0đ) 0,25 Lại có  = 
MAC EBC (hai góc cùng phụ với  ACB ) ⇒  =  MBC EBC 0,25
⇒ BC là tia phân giác của  EBM . 0,25
3) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF . Chứng minh rằng IE là tiếp
tuyến của đường tròn ngoại tiếp tam giác BCE .
Gọi K là trung điểm BC suy ra K là tâm đường tròn ngoại tiếp tam giác BCE . 0,25 3.
Tam giác IAE cân tại ⇒  =  I IAE IEA (1,0đ) 0,25
Tam giác KCE cân tại ⇒  =  K KEC KCE Mà  +  o
DAC DCA = 90 ⇒  +  o IEA KEC = 90 0,25 ⇒  o IEK = 90 0,25
Suy ra IE là tiếp tuyến với đường tròn ngoại tiếp tam giác BCE .
4) Khi hai điểm B, C cố định và điểm A di động trên đường tròn ( ; O R) nhưng
vẫn thỏa mãn điều kiện tam giác ABC có ba góc nhọn. Chứng minh OA  EF.
Xác định vị trí của điểm A để tổng DE  EF  FD đạt giá trị lớn nhất. 4. (1,0đ)
Do tứ giác BCEF nội tiếp (2 đỉnh E,F cùng nhìn cạnh BC dưới 1góc 0,25 vuông) nên  = 
AFE ACB (cùng bù với  BFE ).
Vẽ tiếp tuyến Ax của đường tròn ( ; O R). Ta có Ax ⊥ . OA  = 
xAB ACB (cùng chắn cung  AB ). 0,25 ⇒  = 
xAB AFE ⇒ Ax / /EF. ⇒ EF ⊥ . OA 1 1 ⇒ S + S = OA EF = R EF AOE AOF . . . 2 2 Chứng minh tương tự 1 S + S = R DF 1 S + S = R DE COD COE . . BOF BOD . . 2 2 1 ⇒ S
= R DE + EF + FD ABC .( ). 2 1 1 ⇒ BC.AD = .
R (DE + EF + FD). 0,25 2 2 Trang 3/4 BC ⇒ + + = . BC DE EF FD AD ≤ AK. R R  2 
Mà AK ≤ AO + OK BC BC 2 ⇒ . BC AK ≤  R + R − . R R  4     0,25 2 BC  2 BC
⇒ DE + EF + FD ≤  R + R −  không đổi. R  4   
Dấu “=” xảy ra khi ba điểm ,
A O, K thẳng hàng hay A là điểm chính giữa của cung lớn  BC .
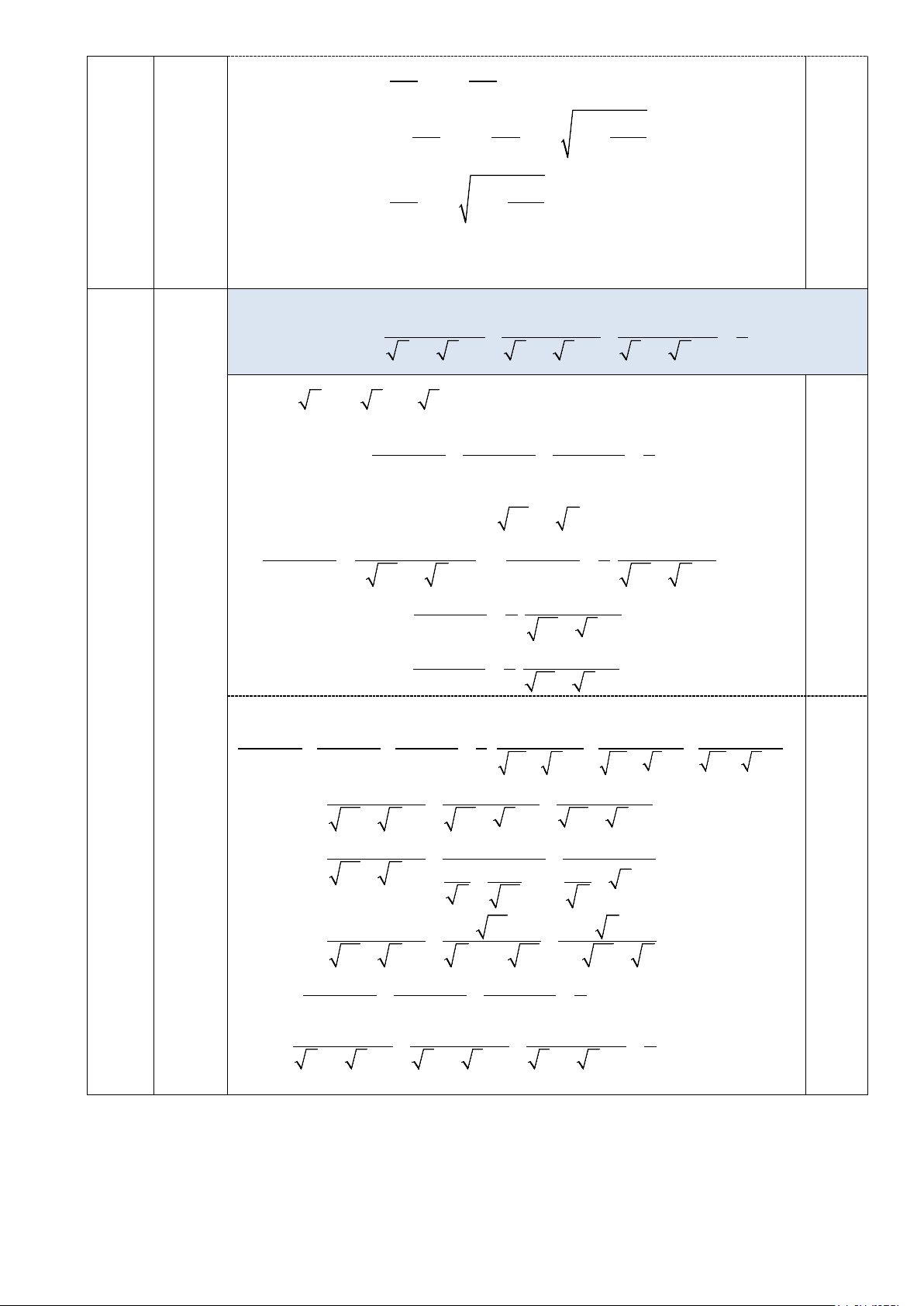
Cho ba số dương a , b , c thỏa mãn abc =1. Chứng minh rằng 1 1 1 1 + + ≤ . a + 2 b + 3 b + 2 c + 3 c + 2 a + 3 2
x, y, z > 0
Đặt x = a , y = b, z = c ⇒  . BĐT cần cm có dạng xyz = 1 1 1 1 1 + + ≤ .
x + 2y + 3 y + 2z + 3 z + 2x + 3 2 Ta có:
x + 2y + 3 = (x + y) + ( y + )
1 + 2 ≥ 2 xy + 2 y + 2 (Áp dụng BĐT Cô si) 0,25 1 1 ⇔ ≤ 1 1 1 ⇔ ≤ .
x + 2y + 3 2 xy + 2 y + 2
x + 2y + 3 2 xy + y +1 Tương tự ta có 1 1 1 ≤ .
y + 2z + 3 2 yz + z +1 1 1 1 ≤ . . Câu 5
z + 2x + 3 2 zx + x +1 (0,5đ) Ta có 1 1 1   + + 1 1 1 1 ≤  + + 
x + 2y + 3 y + 2z +3 z + 2x +3 2  xy y 1 yz z 1 zx x 1 + + + + + +   Mặt khác: 1 1 1 + + xy + y +1 yz + z +1 zx + x +1 1 1 1 = + + xy + y +1 1 1 1 + +1 + x +1 x xy y 0,25 1 xy y = + + = 1 xy + y +1
y +1+ xy 1+ xy + y Do đó 1 1 1 1 + + ≤ .
x + 2y + 3 y + 2z + 3 z + 2x + 3 2 Hay 1 1 1 1 + + ≤ . a + 2 b + 3 b + 2 c + 3 c + 2 a + 3 2
Dấu “=” xảy ra ⇔ a = b = c =1 . ---Hết--- Trang 4/4
Document Outline

• DE TOAN 2020-2021
• HDC 2020-2021