Đề tuyển sinh lớp 10 THPT môn Toán năm 2021 – 2022 sở GD&ĐT Quảng Ngãi

Giới thiệu đến quý thầy, cô giáo và các em học sinh đề tuyển sinh lớp 10 THPT môn Toán năm 2021 – 2022 sở GD&ĐT Quảng Ngãi; kỳ thi được diễn ra vào thứ Sáu ngày 04 tháng 06 năm 2021. Mời bạn đọc đón xem!

39 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

8 trang 8 tháng trước

Tác giả:

Profile Vũ Hường
Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NGÃI
ĐỀ CHÍNH THỨC
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2021-2022
Ngày thi: 04/6/20221
Môn: TOÁN
Thời gian làm bài: 120 phút
Bài 1: (2,0 điểm)
1. Thực hiện phép tính:
7 16 2 9+
.
2. Cho hàm số
2
yx=
có đồ thị
( )
P
.
a) Vẽ
( )
P
.
b) Bằng phép tính, tìm tọa độ các giao điểm của
( )
P
và đường thẳng
.
Bài 2: (2,0 điểm)
1. Giải phương trình và hệ phương trình sau:
a)
2
12 0
xx
+− =
b)
23
34
xy
xy
−=−
+=
.
2. Cho phương trình (ẩn
x
):
( )
22
2 2 70x m xm− + + +=
.
a) Tìm
m
để phương trình có 2 nghiệm phân biệt.
b) Gọi
12
,xx
là hai nghiệm phân biệt của phương trình. Tìm
m
để
22
1 2 12
12
x x xx+= +
.
Bài 3: (1,5 điểm)
Quãng đường
AB
gồm một đoạn lên dốc dài 4 km,
một đoạn bằng phẳng dài 3 km và một đoạn xuống
dốc dài 6 km (như hình vẽ). Một người đi xe đạp từ
A
đến
B
và quay về
A
ngay hết tổng cộng 130 phút.
Biết rằng vận tốc người đó đi trên đoạn đường bằng
phẳng là 12 km/h và vận tốc xuống dốc lớn hơn vận tốc lên dốc 5 km/h (vận tốc lên dốc, xuống
dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc của người đó.
Bài 4: (3,5 điểm)
Cho đường tròn
( )
;OR
và điểm
S
nằm bên ngoài đường tròn,
SO d=
. Kẻ các tiếp tuyến
,SA SB
với đường tròn (
,AB
là các tiếp điểm).
a) Chứng minh rằng 4 điểm
,,,
SOAB
cùng thuộc một đường tròn.
b) Trong trường hợp
2dR=
, tính độ dài đoạn thẳng
AB
theo
R
.
c) Gọi
C
là điểm đối xứng của
B
qua
O
. Đường thẳng
SC
cắt đường tròn
( )
O
tại
D
(khác
C
). Hai đường thẳng
AB
và
SO
cắt nhau tại
M
. Chứng minh rằng
2
.
SM MD MA=
.
d) Tìm mối liên hệ giữa
d
và
R
để tứ giác
OAMB
là hình thoi.
Bài 5: (1,0 điểm)
Cho
x
là số thực bất kỳ. Tìm giá trị nhỏ nhất của biểu thức
22
2
2
73
7
3
xx
T
x
x
++
= +
+
+
HẾT
Ghi chú: Cán bộ coi thi không giải thích gì thêm.
6km
3km
4 km
B
A
Trang 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
QUẢNG NGÃI
ĐỀ CHÍNH THỨC
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2021-2022
Môn: TOÁN
ĐÁP ÁN THAM KHẢO
Bài 1: (2,0 điểm)
1. Thực hiện phép tính:
7 16 2 9+
.
2. Cho hàm số
2
yx=
có đồ thị
(
)
P
.
a) Vẽ
( )
P
.
b) Bằng phép tính, tìm tọa độ các giao điểm của
( )
P
và đường thẳng
.
Lời giải
1.
7 16 2 9 7.4 2.3 28 6 34+ = + = +=
.
2. a) Vẽ đồ thị hàm số
( )
2
yxP=
, ta có bảng sau:
x
-2
-1
0
1
2
2
yx=
4 1 0 1 4
Vậy đồ thị hàm số
( )
2
yxP
=
là Pa-ra-bol đi qua
( ) ( ) ( ) ( ) ( )
2;4, 1;1,0:0,1;1,2;4−−
và nhận
Oy
làm trục đối xứng.
b) Hoành độ giao điểm của
(
)
2
:Pyx=
và
là nghiệm của phương trình:
2
2xx=−+
2
20xx⇔ +−=
Vì
( )
11 2 0
abc+ + =++− =
nên phương trình có hai nghiệm
12
1; 2
c
xx
a
= = = −
.
Với
1
11
1 11xy=⇒==
.
Với
( )
2
22
2 24xy=−⇒ =− =
.
Vậy ta có hai giao điểm của
( )
P
và
( )
d
là
( )
1;1
và
( )
2; 4−
.
6
4
2
5
5
2
1
-1
-2
1
y
x
f
x
( )
=
x
2
O
Trang 3
Bài 2: (2,0 điểm)
1. Giải phương trình và hệ phương trình sau:
a)
2
12 0xx+− =
b)
23
34
xy
xy
−=−
+=
.
2. Cho phương trình (ẩn
x
):
( )
22
2 2 70x m xm
− + + +=
.
a) Tìm
m
để phương trình có 2 nghiệm phân biệt.
b) Gọi
12
,xx
là hai nghiệm phân biệt của phương trình. Tìm
m
để
22
1 2 12
12x x xx+= +
.
Lời giải
1. Giải phương trình và hệ phương trình sau:
a)
2
12 0xx+− =
( )
2
1 4.1. 12 49 0∆= − − = > ⇒
phương trình có hai nghiệm phân biệt
1
1 49
3
2.1
x
−+
= =
;
12
1 49
4
2.1
x
−−
= = −
.
Vậy phương trình có tập nghiệm là
{
}
3; 4
S = −
.
b)
11 11
2323711
77
3 4 2 6 8 4 3 11 5
4 3.
77
yy
xy xy y
xy xy x y
xx

= =

−=− −=− =


⇔ ⇔⇔ ⇔

+= += =− −


=−=


.
Vậy hệ phương trình có tập nghiệm là
5 11
;
77
S
−

=




.
2. Xét phương trình (ẩn
x
):
( )
22
2 2 70x m xm− + + +=
(1).
a) Để phương trình (1) có hai nghiệm phân biệt thì
( )
( )
2
2 22
0 2 1. 7 0 4 4 7 0m m mm m
′
∆>⇔− + − + >⇔ + +− −>


3
4 30 4 3
4
m mm⇔ −>⇔ >⇔ >
.
Vậy
3
4
m
>
thì phương trình (1) có hai nghiệm phân biệt
12
;xx
.
b) Với
3
4
m >
thì phương trình (1) có hai nghiệm phân biệt
12
;xx
, theo hệ thức Vi-et, ta có:
( )
12
2
12
22
.7
xx m
xx m
+= +
= +
.
Theo bài ra ta có:
( )
2
22 22
1 2 12 1 2 12 1 2 12
12 12 0 3 12 0x x xx x x xx x x xx+= +⇔+− −=⇔ + − −=
.
Thay hệ thức Vi-et vào ta có:
( )
( )
2
2
2 2 3 7 12 0mm+ − +−=


22
4 16 16 3 21 12 0mm m⇔ + +− −−=
Trang 4
2
16 17 0mm
⇔ + −=
Vì
( )
1 16 17 0abc+ + =+ +− =
nên phương trình có hai nghiệm:
1
1m
=
(thỏa mãn);
2
17m = −
(loại).
Vậy
1
1m =
là giá trị cần tìm.
Bài 3: (1,5 điểm)
Quãng đường
AB
gồm một đoạn lên dốc dài 4 km,
một đoạn bằng phẳng dài 3 km và một đoạn xuống
dốc dài 6 km (như hình vẽ). Một người đi xe đạp từ
A
đến
B
và quay về
A
ngay hết tổng cộng 130 phút.
Biết rằng vận tốc người đó đi trên đoạn đường bằng
phẳng là 12 km/h và vận tốc xuống dốc lớn hơn vận tốc lên dốc 5 km/h (vận tốc lên dốc, xuống
dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc của người đó.
Lời giải
Gọi vận của người đi xe đạp lúc lên dốc là
x
(km/h), (
0x >
).
Ta có vận tốc của người đi xe đạp lúc xuống dốc là
5x +
(km/h).
Thời gian đi đoạn lên dốc là:
4 6 10
xx
+
=
(h).
Thời gian đi đoạn bằng phẳng là:
33 1
12 2
+
=
(h).
Thời gian đi đoạn xuống dốc là:
6 4 10
55xx
+
=
++
(h).
Vì tổng thời gian đi và về hết 130 phút
13
6
=
giờ nên ta có phương trình:
10 1 10 13 10 10 10 1 1 1
2 5 6 5 6 56x x x x xx
++=⇔+=⇔+=
+ ++
(
) ( )
22
6 5 6 5 6 30 6 5 7 30 0
x xxx x xx x x x⇒ ++= +⇔++=+⇔−−=
Giải phương trình ta được
1
3x = −
(loại);
2
10x =
(thỏa mãn).
Vậy vận của người đi xe đạp lúc lên dốc là
10 /km h
, vận tốc của người đi xe đạp lúc xuống
dốc là
15 /km h
.
Bài 4: (3,5 điểm)
Cho đường tròn
( )
;OR
và điểm
S
nằm bên ngoài đường tròn,
SO d=
. Kẻ các tiếp tuyến
,SA SB
với đường tròn (
,AB
là các tiếp điểm).
a) Chứng minh rằng 4 điểm
,,,SOAB
cùng thuộc một đường tròn.
b) Trong trường hợp
2
dR=
, tính độ dài đoạn thẳng
AB
theo
R
.
c) Gọi
C
là điểm đối xứng của
B
qua
O
. Đường thẳng
SC
cắt đường tròn
( )
O
tại
D
(khác
C
). Hai đường thẳng
AB
và
SO
cắt nhau tại
M
. Chứng minh rằng
2
.
SM MD MA=
.
d) Tìm mối liên hệ giữa
d
và
R
để tứ giác
OAMB
là hình thoi.
Lời giải
6km
3km
4 km
B
A
Trang 5
a) Chứng minh rằng 4 điểm
,,,SOAB
cùng thuộc một đường tròn.
Ta có
,SA SB
là hai tiếp tuyến của
( )
O
90SAO SBO⇒==°
(tính chất của tiếp tuyến)
⇒
4
điểm
,,,SOAB
cùng thuộc đường tròn đường kính
SO
.
b) Trong trường hợp
2dR=
, tính độ dài đoạn thẳng
AB
theo
R
.
Theo tính chất hai tiếp tuyến cắt nhau, ta có
SA SB
=
mà
OA OB=
(bán kính của
( )
O
)
SO⇒
là trung trực của
AB SO AB
⇒⊥
tại trung điểm
H
của
2AB AB AH⇒=
;
Trong
SAO∆
vuông tại
A
, theo định lý Pi-ta-go, ta có
( )
2
2 22 2 2 2
23SO AO SA SA SO AO R R R= + ⇒= − = −=
.
Trong
SAO∆
vuông tại
A
, có
AH
là đường cao, theo hệ thức lượng, ta có
. 3. 3
..
22
SA AO R R R
AH SO SA AO AH
SO R
= ⇒= = =
;
3
2 2. 3
2
R
AB AH R⇒= = =
.
Vậy
3AB R=
.
c) Gọi
C
là điểm đối xứng của
B
qua
O
. Đường thẳng
SC
cắt đường tròn
(
)
O
tại
D
(khác
C
). Hai đường thẳng
AB
và
SO
cắt nhau tại
M
. Chứng minh rằng
2
.SM MD MA=
.
B
A
O
S
R
2R
H
B
A
O
S
Trang 6
Xét
MSD∆
và
MAS∆
có:
M
chung;
Vì
C
đối xứng với
B
qua
O ⇒
O
là trung điểm của
BC
BC⇒
là đường kính của
(
)
O
90BAC⇒=°
(góc nội tiếp chắn nửa đường tròn)
//AC AB AC SO⇒⊥⇒
(cùng vuông góc
với
AB
)
MSD DCA⇒=
(hai góc so le trong);
DCA MAS=
(góc nội tiếp và góc tạo bởi tia
tiếp tuyến và dây cung cùng chắn
AD
)
( )
MSD MAS DCA⇒= =
( )
2
..
MS MA
MSD MAS g g MS MD MA
MD MS
⇒∆ ∆ ⇒ = ⇒ =
”
.
d) Tìm mối liên hệ giữa
d
và
R
để tứ giác
OAMB
là hình thoi.
Tứ giác
OAMB
là hình thoi
AB⇒
là phân giác của
MAO
MAB OAB⇒=
(tính chất của hình
thoi);
MAB DCB=
(hai góc nội tiếp cùng chắn
DB
);
OAB OSB=
(hai góc nội tiếp cùng chắn
OB
)
( )
DCB OSB MAB OAB⇒===
;
Xét
BOS∆
và
BSC
∆
có:
B
chung;
BSO BCS=
(chứng minh trên)
( )
22
. . .2 2
BO BS
BOS BSC g g BS BO BC R R R
BS BC
⇒∆ ∆ ⇒ = ⇒ = = =”
.
Trong
SBO∆
vuông tại
B
, theo định lý Pi-ta-go, ta có:
2 2 2 2 22 2
23 3SO SB OB SO R R R SO R= + ⇒ = += ⇒ =
.
Vậy
3dR=
thì tứ giác
OAMB
là hình thoi.
M
D
C
B
A
O
S
M
D
C
B
A
O
S
Trang 7
Bài 5: (1,0 điểm)
Cho
x
là số thực bất kỳ. Tìm giá trị nhỏ nhất của biểu thức
22
2
2
73
7
3
xx
T
x
x
++
= +
+
+
Lời giải
Với
x
là số thực bất kì, áp dụng bất đẳng thức AM-GM ta có:
22
22
22 2 2
7 34 4 4
3 2 3. 4
33 3 3
xx
xx
xx x x
+ ++
= = ++ ≥ + =
++ + +
.
Từ đó:
22
2
2
73
7
3
xx
T
x
x
++
= +
+
+
2 2 2 22
22
22 2
15 7 1 7 3 15 1 7 3 15 2 17
. . .4 2 . .
16 16 7 16 16 7 4 4 4
33 3
x x x xx
xx
xx x

+ + + ++
= + + ≥ + = +=


++
++ +

.
⇒
17
4
MinT
=
khi
2
2
22
2
4 2 2 42
22
2
2
4
3
3
34 1
11
14 49 16 48 2 1 0
17 3
.
16 7
3
x
x
xx
xx
x x x xx
xx
x
x
+=

+
+= =

⇔ ⇔ ⇔ =⇔=±

+ + = + − +=
++


=
+
+
.
Vậy
17
4
MinT
=
khi
1x = ±
.
HẾT
| 1/8
| | Tải xuống

Có thể bạn quan tâm:

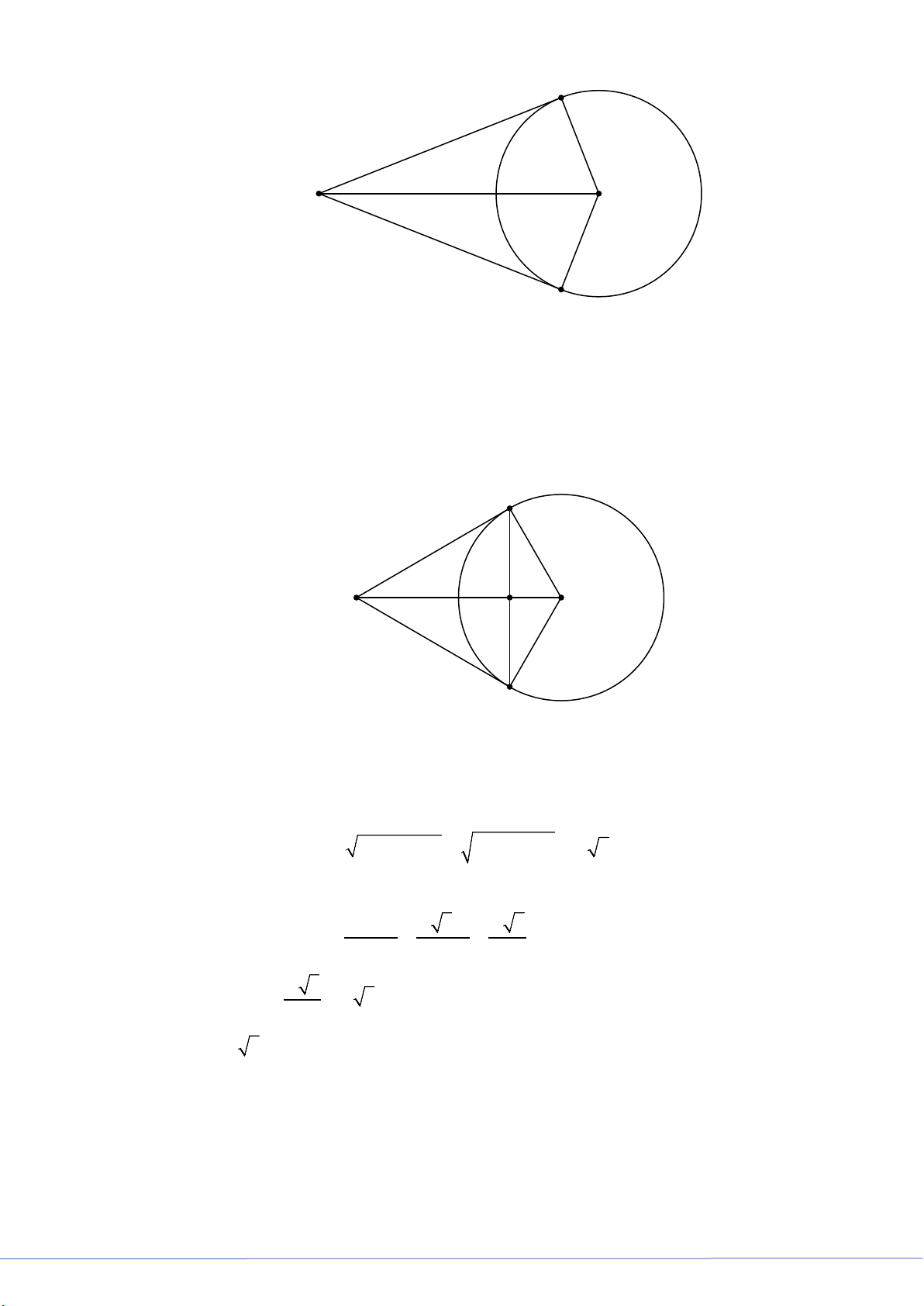
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT QUẢNG NGÃI NĂM HỌC 2021-2022 ĐỀ CHÍNH THỨC Ngày thi: 04/6/20221 Môn: TOÁN
Thời gian làm bài: 120 phút
Bài 1: (2,0 điểm)
1. Thực hiện phép tính: 7 16 + 2 9 . 2. Cho hàm số 2
y = x có đồ thị (P) . a) Vẽ (P) .
b) Bằng phép tính, tìm tọa độ các giao điểm của (P) và đường thẳng (d ) : y = −x + 2 .
Bài 2: (2,0 điểm)
1. Giải phương trình và hệ phương trình sau: 2x − y = 3 − a) 2 x + x −12 = 0 b)  . x + 3y = 4
2. Cho phương trình (ẩn x ): 2 x − (m + ) 2 2
2 x + m + 7 = 0.
a) Tìm m để phương trình có 2 nghiệm phân biệt.
b) Gọi x , x là hai nghiệm phân biệt của phương trình. Tìm m để 2 2
x + x = x x +12 . 1 2 1 2 1 2
Bài 3: (1,5 điểm) 3km
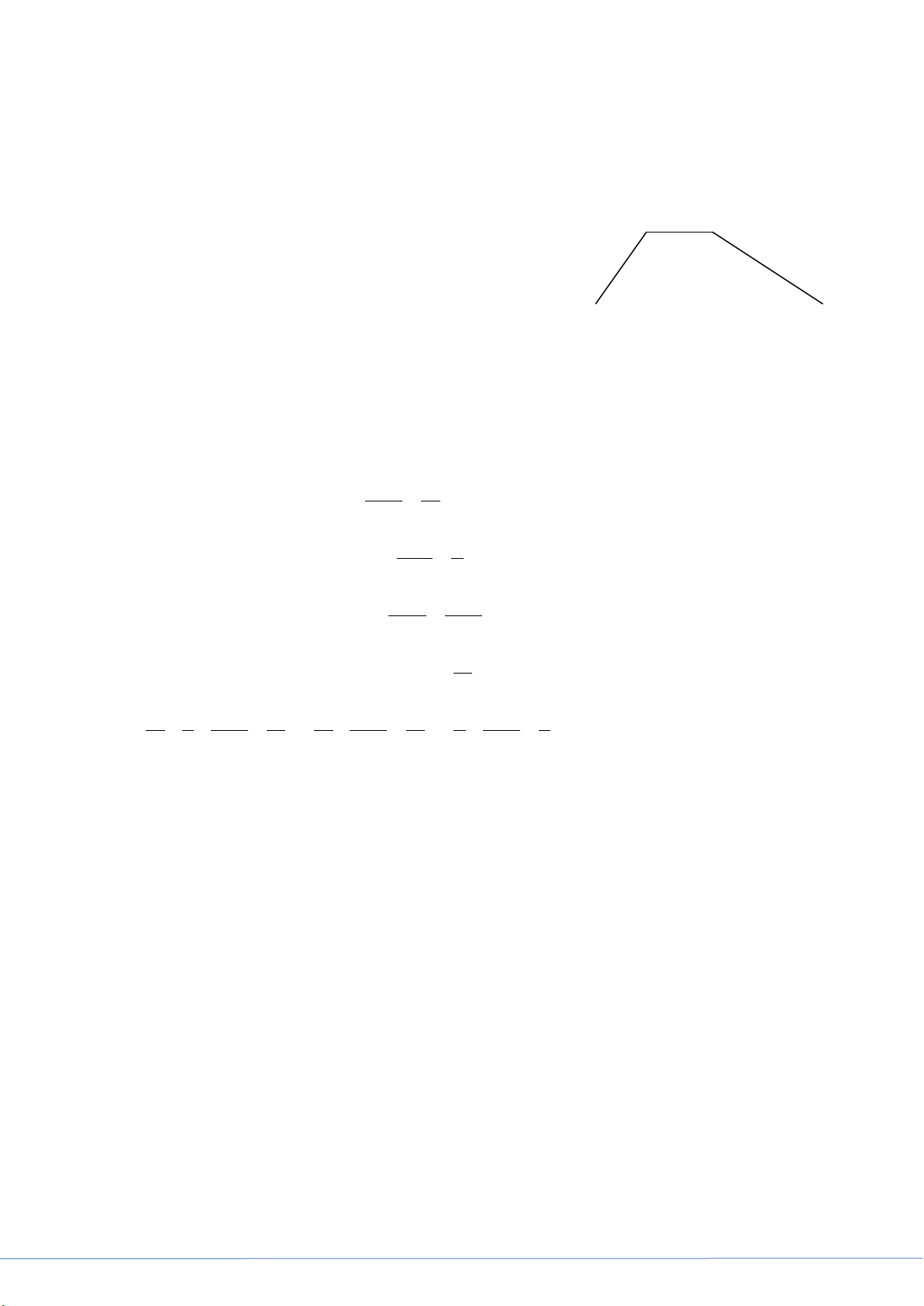
Quãng đường AB gồm một đoạn lên dốc dài 4 km,
một đoạn bằng phẳng dài 3 km và một đoạn xuống 4 km 6km
dốc dài 6 km (như hình vẽ). Một người đi xe đạp từ
A đến B và quay về A ngay hết tổng cộng 130 phút. A B
Biết rằng vận tốc người đó đi trên đoạn đường bằng
phẳng là 12 km/h và vận tốc xuống dốc lớn hơn vận tốc lên dốc 5 km/h (vận tốc lên dốc, xuống
dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc của người đó.
Bài 4: (3,5 điểm) Cho đường tròn ( ;
O R) và điểm S nằm bên ngoài đường tròn, SO = d . Kẻ các tiếp tuyến ,
SA SB với đường tròn ( ,
A B là các tiếp điểm).
a) Chứng minh rằng 4 điểm S,O, ,
A B cùng thuộc một đường tròn.
b) Trong trường hợp d = 2R , tính độ dài đoạn thẳng AB theo R .
c) Gọi C là điểm đối xứng của B qua O . Đường thẳng SC cắt đường tròn (O) tại D (khác
C ). Hai đường thẳng AB và SO cắt nhau tại M . Chứng minh rằng 2 SM = . MD MA.
d) Tìm mối liên hệ giữa d và R để tứ giác OAMB là hình thoi.
Bài 5: (1,0 điểm) 2 2 + +
Cho x là số thực bất kỳ. Tìm giá trị nhỏ nhất của biểu thức x 7 x 3 T = + 2 2 x + 3 x + 7 HẾT
Ghi chú: Cán bộ coi thi không giải thích gì thêm. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT QUẢNG NGÃI NĂM HỌC 2021-2022 ĐỀ CHÍNH THỨC Môn: TOÁN ĐÁP ÁN THAM KHẢO
Bài 1: (2,0 điểm)
1. Thực hiện phép tính: 7 16 + 2 9 . 2. Cho hàm số 2
y = x có đồ thị (P) . a) Vẽ (P) .
b) Bằng phép tính, tìm tọa độ các giao điểm của (P) và đường thẳng (d ) : y = −x + 2 . Lời giải
1. 7 16 + 2 9 = 7.4 + 2.3 = 28 + 6 = 34.
2. a) Vẽ đồ thị hàm số 2
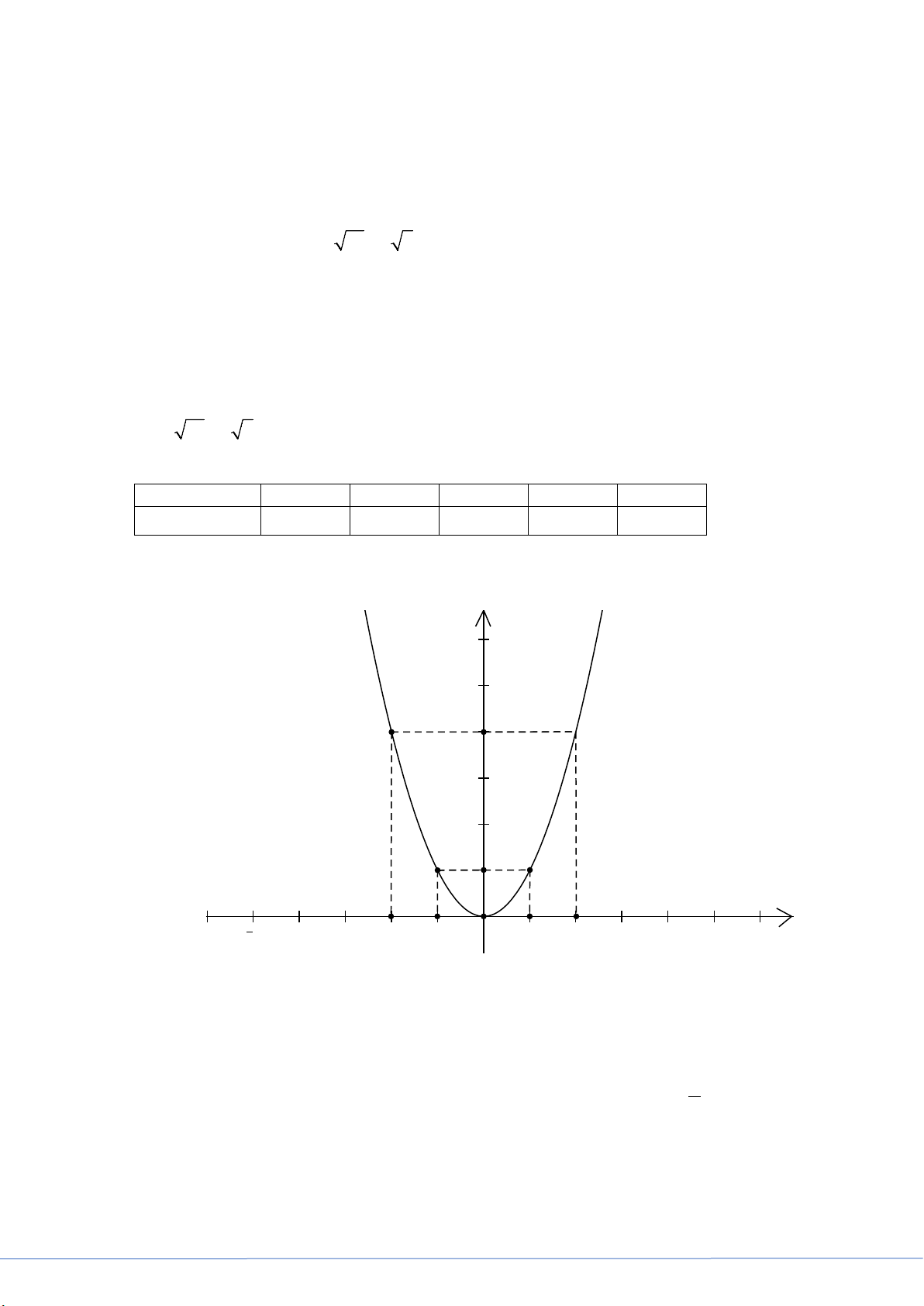
y = x (P) , ta có bảng sau: x -2 -1 0 1 2 2 y = x 4 1 0 1 4 Vậy đồ thị hàm số 2
y = x (P) là Pa-ra-bol đi qua ( 2 − ;4),( 1 − ; ) 1 ,(0 : 0),(1; ) 1 ,(2;4) và nhận
Oy làm trục đối xứng. y 6 f x ( ) = x2 4 2 1 x 5 -2 -1 O 1 2 5
b) Hoành độ giao điểm của (P) 2
: y = x và (d ) : y = −x + 2 là nghiệm của phương trình: 2 x = −x + 2 2
⇔ x + x − 2 = 0
Vì a + b + c =1+1+ ( 2
− ) = 0 nên phương trình có hai nghiệm =1; c x x = = 2 − . 1 2 a Với 1
x =1⇒ y =1 =1. 1 1 Với x = 2 − ⇒ y = ( 2 − )2 = 4 . 2 2
Vậy ta có hai giao điểm của (P) và (d ) là (1; ) 1 và ( 2; − 4) . Trang 2
Bài 2: (2,0 điểm)
1. Giải phương trình và hệ phương trình sau: 2x − y = 3 − a) 2 x + x −12 = 0 b)  . x + 3y = 4
2. Cho phương trình (ẩn x ): 2 x − (m + ) 2 2
2 x + m + 7 = 0.
a) Tìm m để phương trình có 2 nghiệm phân biệt.
b) Gọi x , x là hai nghiệm phân biệt của phương trình. Tìm m để 2 2
x + x = x x +12 . 1 2 1 2 1 2 Lời giải
1. Giải phương trình và hệ phương trình sau: a) 2 x + x −12 = 0 2 ∆ = 1 − 4.1.( 12
− ) = 49 > 0 ⇒ phương trình có hai nghiệm phân biệt 1 49 x − + = = 3 ; 1 49 x − − = = 4 − . 1 2.1 12 2.1
Vậy phương trình có tập nghiệm là S = {3;− } 4 .  11  11 2 − = 3 − 2 − = 3 − 7 =11 y = y x y x y y =   b)  7  7  ⇔  ⇔  ⇔  ⇔ . x 3y 4 2x 6y 8 x 4 3y 11  + = + = = − 5 x − 4 3.  = − x =  7  7
Vậy hệ phương trình có tập nghiệm là  5 11 S  −  =  ; .   7 7  
2. Xét phương trình (ẩn x ): 2 x − (m + ) 2 2
2 x + m + 7 = 0 (1).
a) Để phương trình (1) có hai nghiệm phân biệt thì ∆′ > ⇔ −  (m + ) 2  −  ( 2 m + ) 2 2 0 2 1.
7 > 0 ⇔ m + 4m + 4 − m − 7 > 0 3
⇔ 4m − 3 > 0 ⇔ 4m > 3 ⇔ m > . 4 Vậy 3
m > thì phương trình (1) có hai nghiệm phân biệt x ; x . 4 1 2 b) Với 3
m > thì phương trình (1) có hai nghiệm phân biệt x ; x , theo hệ thức Vi-et, ta có: 4 1 2
x + x = 2 m + 2 1 2 ( )  . 2
x .x = m + 7 1 2 Theo bài ra ta có: 2 2 2 2
x + x = x x +12 ⇔ x + x − x x −12 = 0 ⇔ x + x − 3x x −12 = 0 . 1 2 1 2 1 2 1 2 ( 1 2)2 1 2
Thay hệ thức Vi-et vào ta có:  (m + ) 2 −  ( 2 2 2 3 m + 7) −12 = 0 2 2
⇔ 4m +16m +16 − 3m − 21−12 = 0 Trang 3 2
⇔ m +16m −17 = 0
Vì a + b + c =1+16 + ( 17
− ) = 0 nên phương trình có hai nghiệm: m =1 (thỏa mãn); m = 17 − 1 2 (loại).
Vậy m =1 là giá trị cần tìm. 1
Bài 3: (1,5 điểm) 3km
Quãng đường AB gồm một đoạn lên dốc dài 4 km,
một đoạn bằng phẳng dài 3 km và một đoạn xuống 4 km 6km
dốc dài 6 km (như hình vẽ). Một người đi xe đạp từ
A đến B và quay về A ngay hết tổng cộng 130 phút. A B
Biết rằng vận tốc người đó đi trên đoạn đường bằng
phẳng là 12 km/h và vận tốc xuống dốc lớn hơn vận tốc lên dốc 5 km/h (vận tốc lên dốc, xuống
dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc của người đó. Lời giải
Gọi vận của người đi xe đạp lúc lên dốc là x (km/h), ( x > 0 ).
Ta có vận tốc của người đi xe đạp lúc xuống dốc là x + 5 (km/h). +
Thời gian đi đoạn lên dốc là: 4 6 10 = (h). x x +
Thời gian đi đoạn bằng phẳng là: 3 3 1 = (h). 12 2 +
Thời gian đi đoạn xuống dốc là: 6 4 10 = (h). x + 5 x + 5
Vì tổng thời gian đi và về hết 130 phút 13 =
giờ nên ta có phương trình: 6 10 1 10 13 10 10 10 1 1 1 + + = ⇔ + = ⇔ + = x 2 x + 5 6 x x + 5 6 x x + 5 6
⇒ (x + ) + x = x(x + ) 2 2 6 5 6
5 ⇔ 6x + 30 + 6x = x + 5x ⇔ x − 7x − 30 = 0
Giải phương trình ta được x = 3
− (loại); x =10 (thỏa mãn). 1 2
Vậy vận của người đi xe đạp lúc lên dốc là 10 km / h , vận tốc của người đi xe đạp lúc xuống
dốc là 15 km / h .
Bài 4: (3,5 điểm) Cho đường tròn ( ;
O R) và điểm S nằm bên ngoài đường tròn, SO = d . Kẻ các tiếp tuyến ,
SA SB với đường tròn ( ,
A B là các tiếp điểm).
a) Chứng minh rằng 4 điểm S,O, ,
A B cùng thuộc một đường tròn.
b) Trong trường hợp d = 2R , tính độ dài đoạn thẳng AB theo R .
c) Gọi C là điểm đối xứng của B qua O . Đường thẳng SC cắt đường tròn (O) tại D (khác
C ). Hai đường thẳng AB và SO cắt nhau tại M . Chứng minh rằng 2 SM = . MD MA.
d) Tìm mối liên hệ giữa d và R để tứ giác OAMB là hình thoi. Lời giải Trang 4 A S O B
a) Chứng minh rằng 4 điểm S,O, ,
A B cùng thuộc một đường tròn. Ta có ,
SA SB là hai tiếp tuyến của (O) ⇒  = 
SAO SBO = 90° (tính chất của tiếp tuyến) ⇒ 4 điểm S,O, ,
A B cùng thuộc đường tròn đường kính SO .
b) Trong trường hợp d = 2R , tính độ dài đoạn thẳng AB theo R . A R S O 2R H B
Theo tính chất hai tiếp tuyến cắt nhau, ta có SA = SB mà OA = OB (bán kính của (O) )⇒ SO
là trung trực của AB ⇒ SO ⊥ AB tại trung điểm H của AB ⇒ AB = 2AH ; Trong S
∆ AO vuông tại A , theo định lý Pi-ta-go, ta có 2 2 2 2 2
SO = AO + SA ⇒ SA = SO − AO = ( R)2 2 2 − R = R 3 . Trong S
∆ AO vuông tại A , có AH là đường cao, theo hệ thức lượng, ta có S . A AO R 3.R R 3
AH.SO = S . A AO ⇒ AH = = = ; SO 2R 2 R 3
⇒ AB = 2AH = 2. = R 3 . 2
Vậy AB = R 3 .
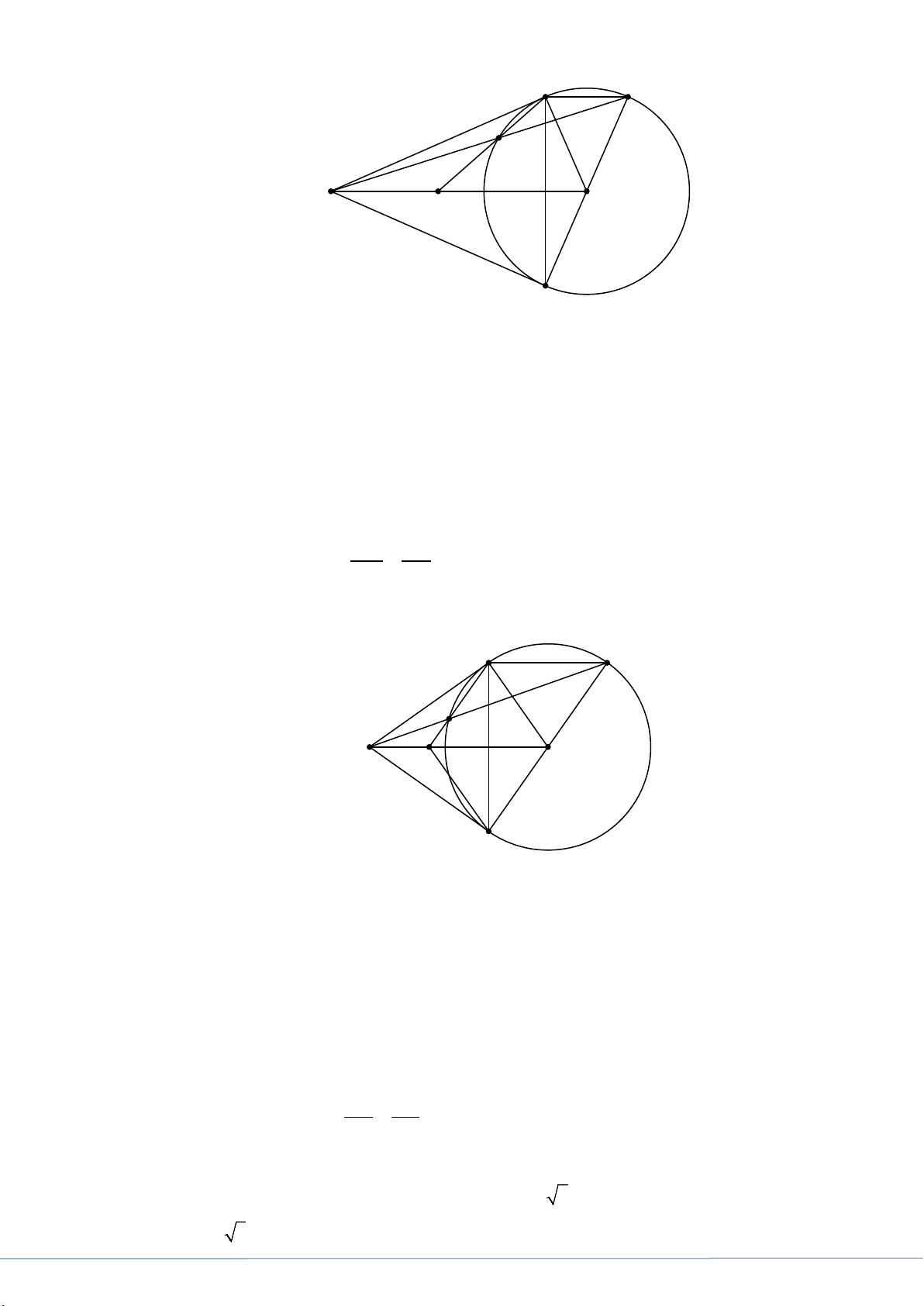
c) Gọi C là điểm đối xứng của B qua O . Đường thẳng SC cắt đường tròn (O) tại D
(khác C ). Hai đường thẳng AB và SO cắt nhau tại M . Chứng minh rằng 2 SM = . MD MA. Trang 5 A C D S O M B Xét MS ∆ D và MA ∆ S có:  M chung;
Vì C đối xứng với B qua O ⇒ O là trung điểm của BC ⇒ BC là đường kính của (O) ⇒ 
BAC = 90° (góc nội tiếp chắn nửa đường tròn) ⇒ AC ⊥ AB ⇒ AC//SO (cùng vuông góc
với AB ) ⇒  = 
MSD DCA (hai góc so le trong);  = 
DCA MAS (góc nội tiếp và góc tạo bởi tia
tiếp tuyến và dây cung cùng chắn 
AD ) ⇒  =  =  MSD MAS ( DCA) ⇒ MS ∆ D” MA ∆ S (g g) MS MA 2 . ⇒ = ⇒ MS = . MD MA . MD MS
d) Tìm mối liên hệ giữa d và R để tứ giác OAMB là hình thoi. A C D S O M B
Tứ giác OAMB là hình thoi ⇒ AB là phân giác của  MAO ⇒  = 
MAB OAB (tính chất của hình thoi);  = 
MAB DCB (hai góc nội tiếp cùng chắn  DB );  = 
OAB OSB (hai góc nội tiếp cùng chắn  OB ) ⇒  =  =  = 
DCB OSB( MAB OAB); Xét B ∆ OS và B ∆ SC có: B chung;  = 
BSO BCS (chứng minh trên) ⇒ B ∆ OS” B ∆ SC (g g) BO BS 2 2 . ⇒ = ⇒ BS = B . O BC = .2 R R = 2R . BS BC Trong S
∆ BO vuông tại B , theo định lý Pi-ta-go, ta có: 2 2 2 2 2 2 2
SO = SB + OB ⇒ SO = 2R + R = 3R ⇒ SO = R 3 .
Vậy d = R 3 thì tứ giác OAMB là hình thoi. Trang 6
Bài 5: (1,0 điểm) 2 2 + +
Cho x là số thực bất kỳ. Tìm giá trị nhỏ nhất của biểu thức x 7 x 3 T = + 2 2 x + 3 x + 7 Lời giải
Với x là số thực bất kì, áp dụng bất đẳng thức AM-GM ta có: 2 2 x + 7 x + 3+ 4 2 4 2 4 = = x + 3 + ≥ 2 x + 3. = 4 . 2 2 2 2 x + 3 x + 3 x + 3 x + 3 Từ đó: 2 2 x + 7 x + 3 T = + 2 2 x + 3 x + 7 2  2 2  2 2 15 x + 7 1 x + 7 x + 3 15 1 x + 7 x + 3 15 2 17 = . +  . +  ≥ .4 + 2 . . = + = . 2 2 2  2 + + +  2
16 x 3 16 x 3 x 7 16 16 x +   3 x + 7 4 4 4 ⇒ 17 MinT = khi 4  2 4 x + 3 =  2 2 2  x + 3 x + 3 = 4 x =1 2  ⇔  ⇔ 
⇔ x =1 ⇔ x = 1 ± . 2 2 4 2 2 4 2  1 x + 7 x + 3
x +14x + 49 =16x + 48
x − 2x +1 = 0 . =  2 2 16  x + 3 x + 7 Vậy 17 MinT = khi x = 1 ± . 4 HẾT Trang 7
Document Outline

  • de-tuyen-sinh-lop-10-thpt-mon-toan-nam-2021-2022-so-gddt-quang-ngai
  • 48. Quảng Ngãi - hoangthinhvanan@gmail.com