Đề tuyển sinh lớp 10 THPT môn Toán năm 2022 – 2023 sở GD&ĐT Hải Dương

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 TRUNG HỌC PHỔ THÔNG HẢI DƯƠNG NĂM HỌC 2022 – 2023 Môn thi: TOÁN
Thời gian làm bài: 120 phút, không tính thời gian phát đề ĐỀ CHÍNH THỨC (Đề thi có 01 trang)
Câu 1 (2,0 điểm). Giải các phương trình sau: a. x  3  2; b. 2 x  3x  6  2x . Câu 2 (2,0 điểm). 3 2 1
a. Rút gọn biểu thức P     với x  0 và x  4 . x  2 x   1 x 1 2  x
b. Tìm giá trị của tham số m để ba đường thẳng sau cắt nhau tại một điểm: 3x  5 y  6  4 ; x y 
và y  (m 1)x  2m  5. 4 Câu 3 (2,0 điểm).
a. Bạn An đi xe đạp từ nhà đến trường trên quãng đường dài 4 km. Khi đi từ trường về
nhà vẫn trên con đường đó, An đạp xe với vận tốc trung bình lớn hơn vận tốc trung bình lúc đi là
3 km/h. Tổng thời gian đạp xe cả đi và về của An là 36 phút. Tính vận tốc đạp xe trung bình của
An lúc đi từ nhà đến trường.
b. Trong mặt phẳng tọa độ Oxy , cho parabol 2
(P) : y  x và đường thẳng (d ) : y  mx  5.
Chứng minh rằng với mọi giá trị của tham số m, đường thẳng (d ) luôn cắt (P) tại hai điểm phân
biệt có hoành độ x , x . Tìm m để 2 x  9  mx . 1 2 1 2 Câu 4 (3,0 điểm).
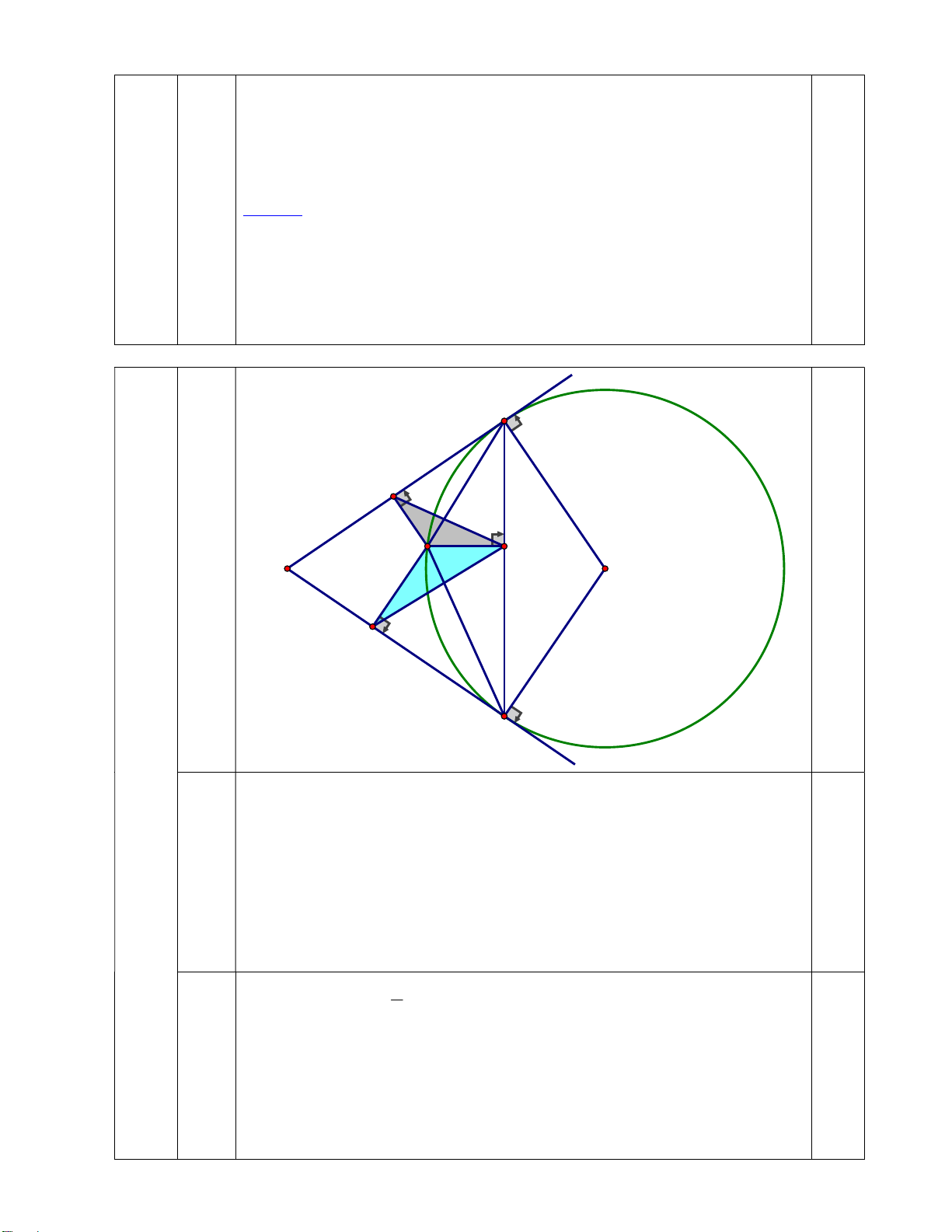
1. Cho đường tròn (O) và dây cung BC không đi qua tâm O. Hai tiếp tuyến với đường tròn
(O) tại B và C cắt nhau tại A. Lấy điểm M trên cung nhỏ BC (M khác B và C), gọi I, H, K theo
thứ tự là chân các đường vuông góc kẻ từ M đến BC, AB, AC.
a. Chứng minh các tứ giác MIBH, MICK nội tiếp; b. Chứng minh 2 MI  MH.MK .
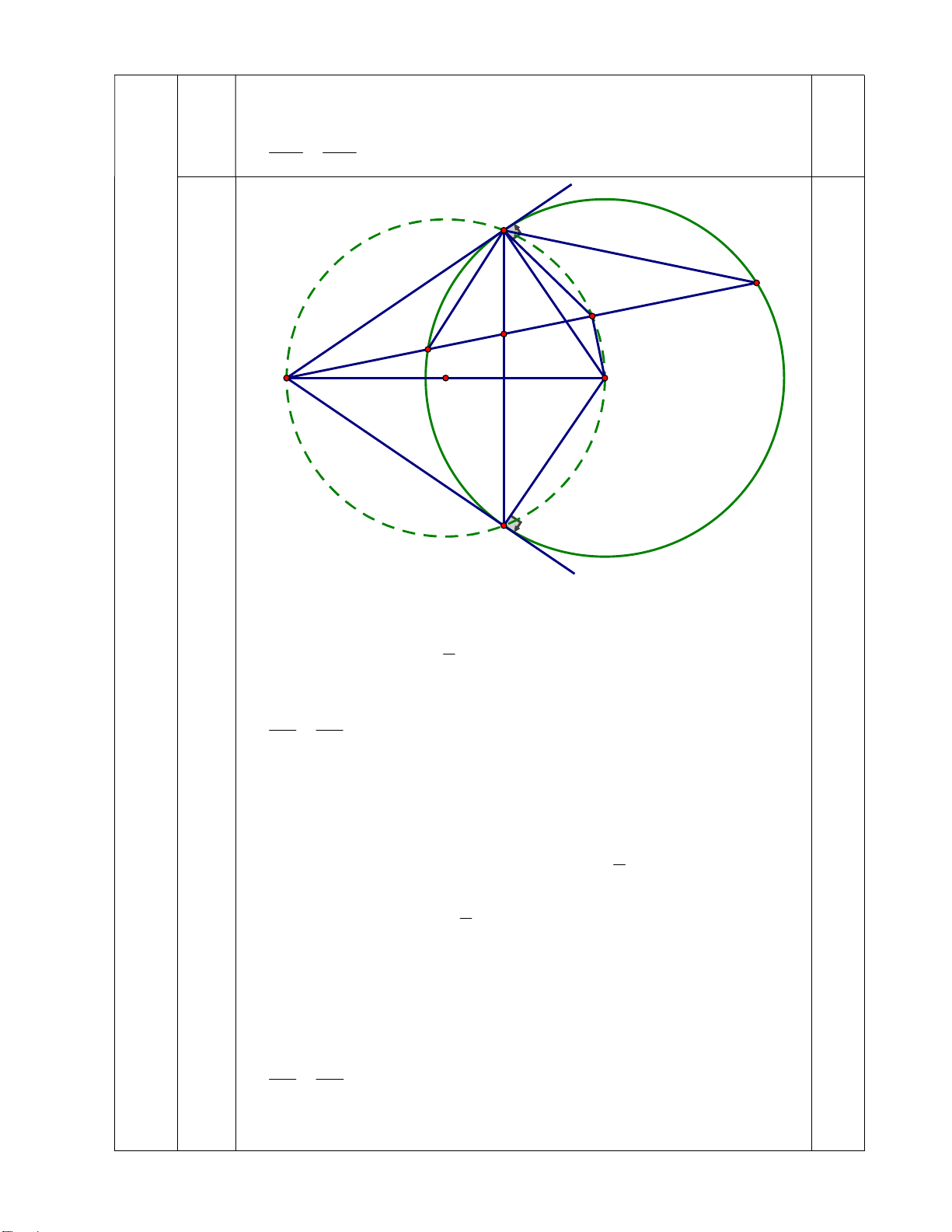
2. Từ điểm P nằm ngoài đường tròn (O) kẻ hai tiếp tuyến PQ, PR tới đường tròn với Q và
R là các tiếp điểm. Đường thẳng qua P cắt đường tròn (O) tại hai điểm E và F (E nằm giữa P và
F; dây cung EF không đi qua tâm O). Gọi I là trung điểm của EF, K là giao điểm của PF và QR. 2 1 1 Chứng minh rằng:   . PK PE PF ab bc ca
Câu 5 (1,0 điểm). Cho a,b,c là các số thực dương thay đổi thỏa mãn    3. c a b 2022
Tìm giá trị nhỏ nhất của biểu thức T  a  b  c  . a  b  c
- - - - - - - - - - HẾT - - - - - - - - - -
(Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh: ………………………………………… Số báo danh: …………… Phòng thi ……
Cán bộ coi thi số 1: ……………………………… Cán bộ coi thi số 2: …………………………………
HƯỚNG DẪN GIẢI VÀ BIỂU ĐIỂM DỰ KIẾN: Câu Phần Nội dung Điểm x  3  2 x  5 x  3  2   a)  x 3 2     x  1 1.00 Câu
Vậy tập nghiệm của phương trình là S  {5;1} 1 2 2
x  3x  6  2x  x  3x  2x  6  0  x(x  3)  2(x  3)  0 (2,0đ) x  3  0 x  3 b)
 (x  3)(x  2)  0    1.00 x 2 0    x  2
Vậy tập nghiệm của phương trình là S  {3;2} 3 2 1 P     x  2 x   1 x 1 2  x 3 2 1     x  2 x   1 x 1 x  2
3  2 x  2 1 x   1   x 2 x  1 a) 3  2 x  4  x 1  1.00  x  2 x   1 x  2
  x 2 x  1 1 Câu  2 x 1 (2,0đ) 1 Vậy P  với x  0 và x  4 . x 1 3x  5 Gọi (d ) : y  6  4 ; x (d ) : y 
; (d ) : y  (m 1)x  2m  5 1 2 3 4 7
Để ba đường thẳng cắt nhau thì m  3  ; m  4
Hoành độ giao điểm của (d ) và (d ) là nghiệm của phương trình: 1 2 3x  5 6  4x 
 24 16x  3x  5  1  9x  1  9  x 1 b) 4 1.00
Tung độ giao điểm của (d ) và (d ) là y  6  4.1  2 1 2
 (d ) cắt (d ) tại điểm ( A 1;2) 1 2
Để ba đường thẳng cắt nhau tại một điểm thì A (d ) 3
 (m 1).1 2m  5  2  m 1 2m  5  2  3m  8 8  m  (TMĐK) 3 8
Vậy m  là giá trị cần tìm. 3
Gọi vận tốc đạp xe trung bình của An lúc đi từ nhà đến trường là x (km/h) (ĐK: x > 0)
 Vận tốc đạp xe trung bình của An lúc đi từ trường về nhà là x + 3 (km/h) 4
Thời gian An đi từ nhà đến trường là (h) x 4
Thời gian An đi từ trường về nhà là (h) x  3 3
Vì tổng thời gian đạp xe cả đi và về của An là 36 phút (= giờ) nên ta 5 a) có phương trình: 1.00 4 4 3   x x  3 5 
20(x  3)  20x  3x(x  3)  2 3x  31x  60  0 x  12 (TMĐK)   5 x   (loại)  3
Vậy vận tốc đạp xe trung bình của An lúc đi từ nhà đến trường là 12 Câu km/h. 3
Xét phương trình hoành độ giao điểm của (P) và (d) : (2,0đ) 2 2
x  mx  5  x  mx  5  0 (1) Vì ac  1.( 5
 )  0 nên phương trình (1) luôn có hai nghiệm phân biệt x , x 1 2
 đường thẳng (d ) luôn cắt (P) tại hai điểm phân biệt x  x  m
Áp dụng hệ thức Vi-ét, ta có: 1 2  (*) x x  5   1 2 Theo đề bài: 2 x  9  mx (2) 1 2 Cách 1: b)
Vì x là nghiệm của phương trình (1) nên: 1.00 1 2 2
x  mx  5  0  x  mx  5 (3) 1 1 1 1 Thay (3) vào (2) được:
mx  5  9  mx  mx  mx  4  m(x  x )  4 1 2 1 2 1 2 Mà x  x  m 1 2 2  .
m m  4  m  4  m  2 
Vậy m  2 là các trị cần tìm. Cách 2:
Vì x là nghiệm của phương trình (1) nên: 2 2 2
x  mx  5  0  mx  x  5 (4) 2 2 2 2 Thay (4) vào (2) được: 2 2 2 2 2
x  9  x  5  x  x  14  (x  x )  2x x  14 (5) 1 2 1 2 1 2 1 2 Thay (*) vào (5) được: 2 2
m 10  14  m  4  m  2
Vậy m  2 là các trị cần tìm. Cách 3: (2) 2
 x  9  (x  x )x (vì x  x  m ) 1 1 2 2 1 2 2 2 2 2 2
 x  9  x x  x  x  x  x x  9  (x  x )  x x  9 (6) 1 1 2 2 1 2 1 2 1 2 1 2 Thay (*) vào (6) được: 2 2
m  5  9  m  4  m  2
Vậy m  2 là các trị cần tìm. B 1 2 H 1 1 M I 2 A O 0.25 1 K 1 2 Câu C 4 (3,0đ) Tứ giác MIBH có:    o MIB MHB  90 (GT)     o MIB MHB  180
 Tứ giác MIBH nội tiếp 1a) 0.75 Tứ giác MICK có:    o MIC MKC  90 (GT)     o MIC MKC  180
 Tứ giác MICK nội tiếp  1  (O) có 1 B   C  sđ  2 MB   (1)  2 
Tứ giác MIBH nội tiếp  1 B  1 I (2)
1b) Tứ giác MICK nội tiếp  C   1.00 2 K1 (3) Từ (1), (2), (3)  1 I   K1
Chứng minh tương tự được I2  1 H  MIH và  MKI có:   1 I   K1 ; I2  1 H   MIH   MKI (g-g) MI MH 2    MI  MH.MK MK MI Q 1 F I 1 K E 1 P O R PQE và PFQ có :  1   Q  F  sđEQ 2) 1 P chung ;    1    2  1.00   PQE   PFQ (g-g) PQ PE 2    PQ  PE.PF (1) PF PQ
(O) có I là trung điểm của dây EF  OI  EF   o PIO  90
PQ, PR là các tiếp tuyến của (O)     o PQO PRO  90
 5 điểm P, Q, I, O, R cùng thuộc đường tròn đường kính PO  1 
Xét đường tròn đường kính PO có 1 I   PRQ  sđ PQ    2   1  Xét (O) có  PQR   PRQ  sđ  QR    2    PQR  1 I PQK và PIQ có : 1 P chung ;  PQR  1 I   PQK   PIQ (g-g) PQ PK 2    PQ  PK.PI (2) PI PQ
Từ (1) và (2)  PE.PF = PK.PI
Mà I là trung điểm EF  PE + PF = 2PI 1 1 PE  PF 2PI 2 Do đó:     PE PF PE.PF PK.PI PK 2 1 1 Vậy   (đpcm) PK PE PF ab bc
Áp dụng BĐT Cô-si cho hai số dương và , ta có: c a ab  bc  ab bc 2   2 b c a c a bc ca ca ab Tương tự:   2 c ;   2 a a b b c  ab bc ca   2     2 a  b  c  c a b    3  a  b  c  0 2013 2013    671 a  b  c 3 9
Áp dụng BĐT Cô-si cho hai số dương a  b  c và , a  b  Câu c 5 ta có: 1.00 (1,0đ)  a  b  c 9    a  b  c 9 2   6 a  b  c a  b  c Do đó: 2022
T  a  b  c  a  b  c    a  b  c  9  2013    6  671  677   a  b  c  a  b  c Dấu “=” xảy ra  ab bc ca     c a b    a  b  c  3  a  b  c  1  9  a  b  c   a  b   c
Vậy minT  677  a  b  c  1
- - - - - - - - - - HẾT - - - - - - - - - - Thầy Nguyễn Mạnh Tuấn
Trường THCS Nguyễn Huệ – Cẩm Giàng – Hải Dương
Document Outline

• de-tuyen-sinh-lop-10-thpt-mon-toan-nam-2022-2023-so-gddt-hai-duong
• 000