Đề tuyển sinh lớp 10 THPT môn Toán năm 2022 – 2023 sở GD&ĐT Lạng Sơn
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi chính thức kỳ thi tuyển sinh vào lớp 10 THPT môn Toán năm học 2022 – 2023 sở Giáo dục và Đào tạo tỉnh Lạng Sơn. Mời các bạn đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT LẠNG SƠN
NĂM HỌC 2022 – 2023 ĐỀ CHÍNH THỨC Môn thi: TOÁN
Thời gian: 120 phút (không kể thời gian phát đề) HƯỚNG DẪN GIẢI
Câu 1. (2,5 điểm)
a. Tính giá trị của các biểu thức: A = 81 − 16 ; B = ( + )2 11 2 − 11 . b. Cho biểu thức: 1 2 2 = + . a P
, với a > 0 và a ≠ 1.
a −1 a − a a + 2
1. Rút gọn biểu thức P
2. Tính giá trị của P khi a = 3+ 2 2 . Lời giải a. Ta có 2 2
A = 81 − 16 = 9 − 4 = 9 − 4 = 5 B = ( + )2
11 2 − 11 = 11 + 2 − 11 = 11 + 2 − 11 = 2.
Vậy A = 5, B = 2. b.
1. Với a > 0 và a ≠ 1 ta có: 1 2 2 a 1 2 2 . a P = + = + a −
a − a a + a − a ( a − ) . 1 2 1 1 a + 2 a + 2 2 a 2 = = a ( a − ). 1 a + 2 a −1 2 2 2. Ta có a = + = ( ) 2 3 2 2
2 + 2. 2.1+1 = ( 2 + )1 ⇒ a = 2 +1 = 2 +1.
Thay a = 2 +1 vào biểu thức P sau thu gọn ta được 2 2 P = = = 2 . a −1 2
Câu 2. (2,0 điểm)
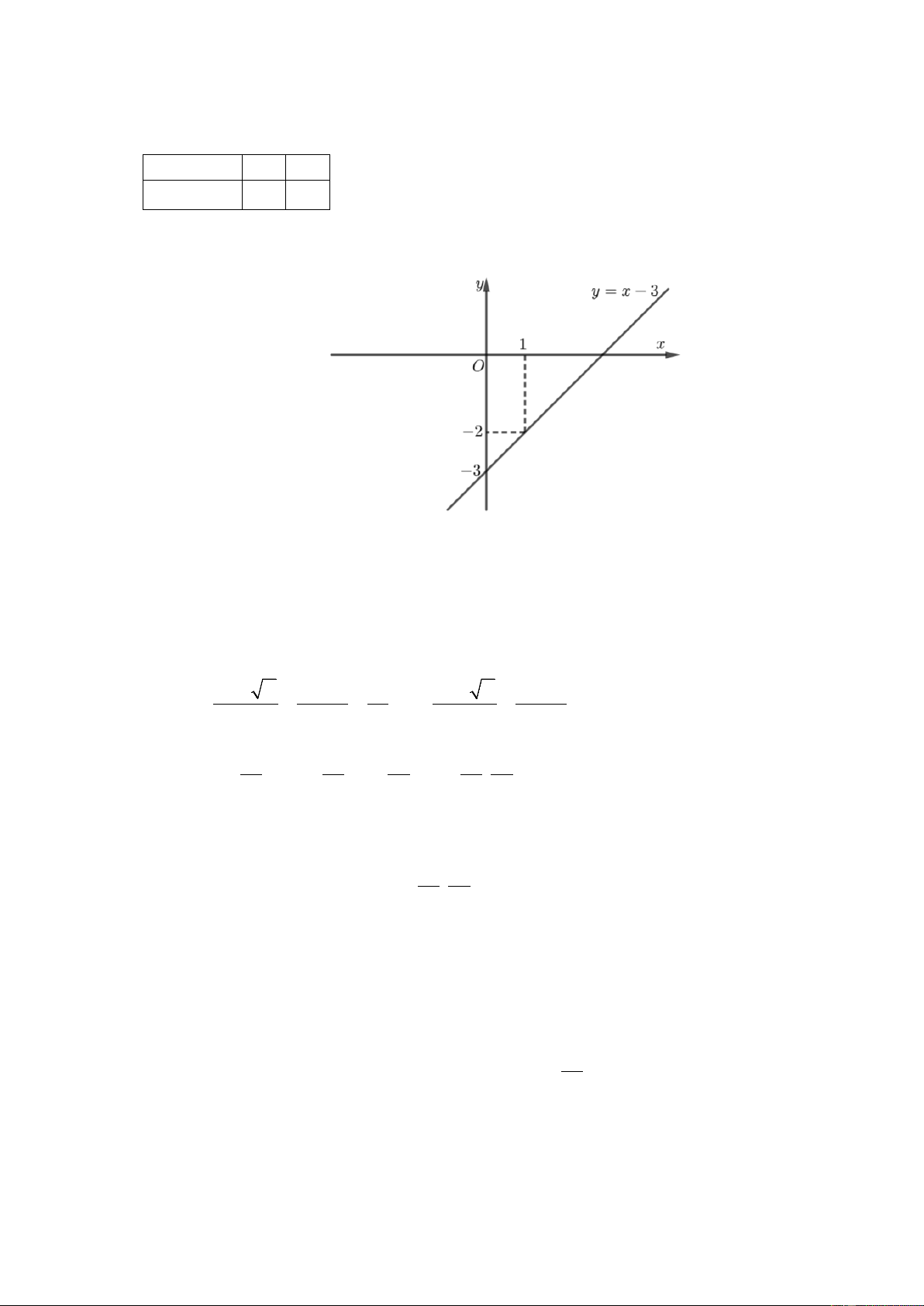
a. Vẽ đồ thị hàm số y = x − 3 .
b. Tìm tọa độ giao điểm của đồ thị hàm số 2 y = 2
− x và đường thẳng y = x − 3 .
c. Cho phương trình bậc hai với tham số 2
m : x − 2(m + )
1 x + 2m − 3 = 0 (1) .
1. Giải phươntg trình (1) khi m = 0.
2. Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt x , x với mọi m . Tìm 1 2
tất cả các giá trị của m thỏa mãn: x + x − 2x x =1. 1 2 1 2 Lời giải
a. Bảng giá trị: (d):y= x−3 x 0 1 y = x − 3 3 − 2 −
Đường thẳng y = x − 3 đi qua 2 điểm A(0; 3 − ) và B(1; 2 − ) . Đồ thị
b. Phương trình hoành độ giao điểm của đồ thị hàm số 2 y = 2
− x và đường thẳng y = x − 3 là 2 2 2
− x = x − 3 ⇔ 2
− x − x + 3 = 0 Ta có ∆ = (− )2 1 − 4.( 2
− ).3 = 25 > 0 nên phương trình trên có hai nghiệm phân biệt − + ∆ + − − − ∆ − b 1 5 3 b 1 5 x = = = ; x = = =1 1 . 2a 2.( 2 − ) 2 2 2a 2.( 2 − ) Với 3 − 3 − 9 − 3 − 9 x y 3 A ; − = ⇒ = − = ⇒ . 1 1 2 2 2 2 2
Với x =1⇒ y =1− 3 = 2 − ⇒ B 1; 2 − . 2 1 ( )
Vậy hai giao điểm cần tìm là 3 9 A − ; − và B(1; 2 − ) . 2 2 c.
1. Thay m = 0 vào phương trình (1) ta có: 2
x − 2x − 3 = 0.
Ta có a − b + c =1− ( 2 − ) + ( 3 − ) = 0.
Suy ra phương trình có hai nghiệm = 1, −c x − x = = 3. 1 2 a
Vậy với m = 0 thì phương trình có tập nghiệm S = { 1; − } 3 .
2. Xét phương trình 2 x − 2(m + )
1 x + 2m − 3 = 0 (1)
Ta có ∆ = (m + )2 −( m − ) 2 ' 1 2
3 = m + 4 > 0 với mọi m .
Khi đó phương trình (1) luôn có 2 nghiệm phân biệt x , x . 1 2
x + x = 2 m +1 1 2 ( )
Áp dụng hệ thức Vi-ét ta có: .
x x = 2m −3 1 2 7
Theo đề x + x − 2x x =1 ⇔ 2 m +1 − 2 2m − 3 =1 ⇔ 2
− m + 8 =1 ⇔ 2m = 7 ⇔ m = 1 2 1 2 ( ) ( ) . 2 7
Vậy m = là giá trị cần tìm. 2
Câu 3. (1,5 điểm)
Giải các phương trình, hệ phương trình sau: 2x + y = 9 a. 4 2
x − 3x + 2 = 0 . b. . x − y = 3 Lời giải a. 4 2
x − 3x + 2 = 0 Đặt 2
t = x ,t ≥ 0.
Khi đó phương trình đã cho trở thành 2t − 3t + 2 = 0 (1)
Phương trình (1) có a + b + c =1+ ( 3
− ) + 2 = 0 nên có hai nghiệm phân biệt là t =1 , t = 2 . 1 2 Với 2
t =1 ⇔ x =1 ⇔ x = 1 ± . 1 Với 2
t = 2 ⇔ x = 2 ⇔ x = ± 2 . 2
Vậy phương trình đã cho có tập nghiệm S = {1; 1; − − 2; 2}. b. 2x + y = 9 2x + y = 9
2( y + 3) + y = 9 ⇔ ⇔ x y 3 x y 3 − = = + x = y + 3 3 y + 6 = 9 y =1 y =1 ⇔ ⇔ ⇔ x y 3 x y 3 = + = + x = 4
Vậy hệ phương trình đã cho có nghiệm ( ; x y) = (4; ) 1
Câu 4. (3,5 điểm)
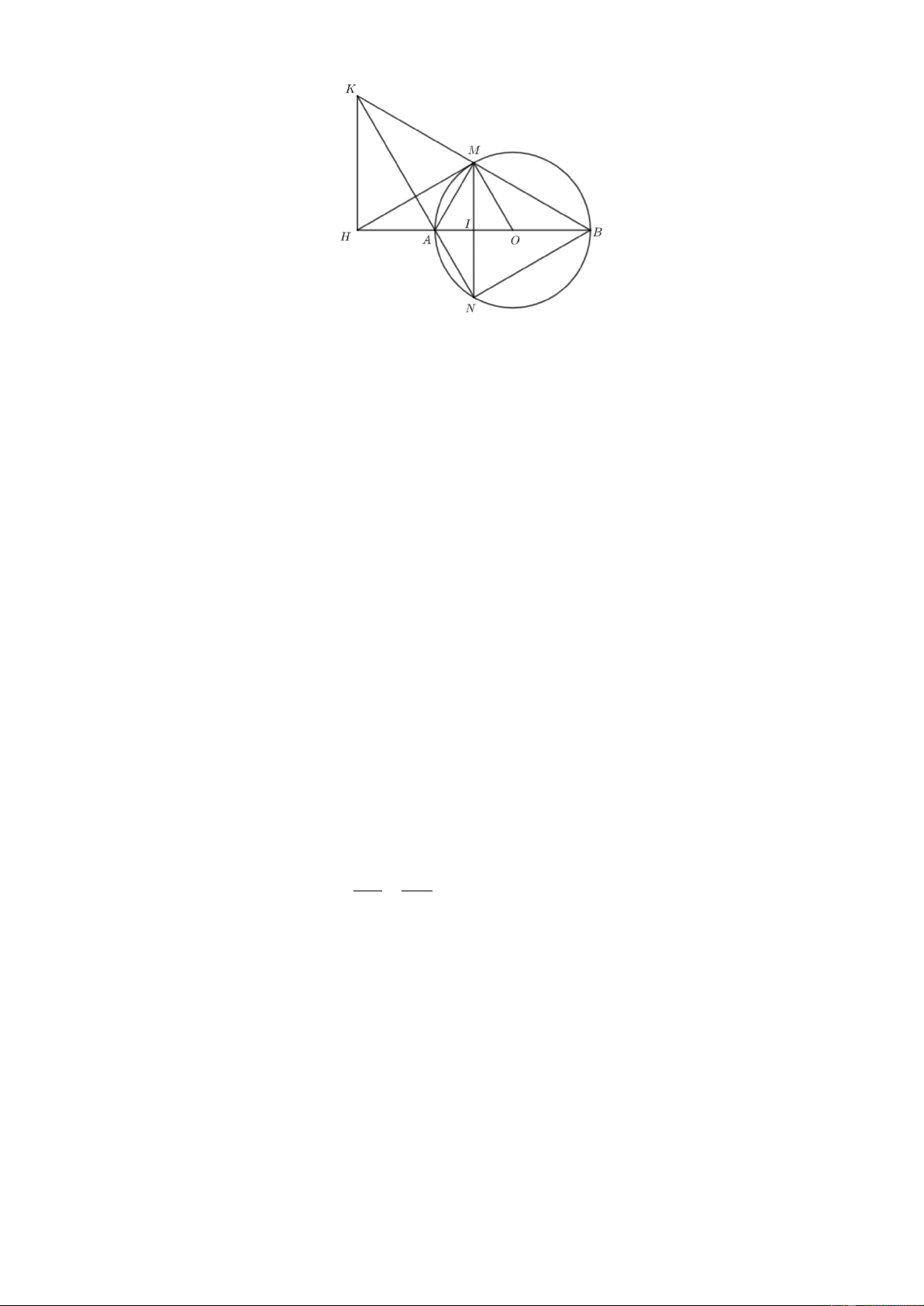
Cho đường tròn (O) đường kính AB . Dây cung MN vuông góc với AB , ( AM < BM ) . Hai
đường thẳng BM và NA cắt nhau tại K . Gọi H là chân đường vuông góc kẻ từ K đến đường thẳng AB .
a. Chứng minh rằng tứ giác AHKM nội tiếp trong một đường tròn.
b. Chứng minh rằng N .
B HK = AN.HB .
c. Chứng minh HM là tiếp tuyến của đường tròn (O) . Lời giải
a. Xét (O) có AMB 90° =
(góc nội tiếp chắn nửa đường tròn)
Xét tứ giác AHKM có AMK AHK 90° 90° 180° + = + =
. Mà 2 góc này ở vị trí đối đỉnh
⇒ Tứ giác AHKM nội tiếp trong một đường tròn. (đpcm) b.
Gọi I = MN ∩ AB .
Vì dây cung MN ⊥ AB tại I nên I là trung điểm của MN .
⇒ AI là đường trung trực của MN .
⇒ AM = AN (tính chất đường trung trực của đoạn thẳng) ⇒ =
AM AN (hai dây bằng nhau chắn hai cung bằng nhau) ⇒ =
MBA NBA (hai góc nội tiếp chắn hai cung bằng nhau) Xét (O) có ANB 90° =
(góc nội tiếp chắn nửa đường tròn) Xét A ∆ NB và K ∆ HB có: +) ANB KHB ( 90° = = ) +) = = ABN HBK ( ABM ) ⇒ ∆ ∆ ( . ) NB AN ANB KHB g g ⇒ = ⇒ N .
B HK = AN.HB (đpcm). HB KH c.
Vì tứ giác AHKM là tứ giác nội tiếp nên =
HMA HKA (hai góc nội tiếp cùng chắn cung HA ) (1) Xét K
∆ HA vuông tại H có KAH HKA 90° + = Xét A
∆ NB vuông tại N có NAB ABN 90° + = . Mà =
KAH NAB (đối đỉnh) ⇒ = HKA ABN (2). Lại có = =
ABM ABN (cmt); ABM BMO (do B
∆ MO cân tại O ) ⇒ = ABN BMO (3)
Từ (1), (2), (3) ⇒ = HMA BMO . Mà AMO BMO AMB 90° + = =
(góc nội tiếp chắn nửa đường tròn) ° AMO HMA 90 HMO 90° ⇒ + = ⇒ =
⇒ HM ⊥ OM tại M .
Vậy HM là tiếp tuyến của đường tròn (O) tại M .
Câu 5. (0,5 điểm)
Cho các số thực dương a,b,c dương. Tìm giá trị lớn nhất của biểu thức sau: a 2b c P = + +
(a +b)(a + c)
(b + c)(b + a)
(c + a)(c +b) Lời giải
Áp dụng bất đẳng thức AM-GM, ta có: a a a ≤ +
(a +b)(a + c) a +b 4(a + c) 2b b b ≤ +
(b + c)(b + a) b + c b + a c c c ≤ +
(c + a)(c +b) 4(c + a) c +b
Cộng vế theo vế các bất đẳng thức trên ta được a 2b c a a b b c c + + ≤ + + + + +
(a +b)(a + c)
(b + c)(b + a)
(c + a)(c +b) a +b 4(a + c) b + c b + a 4(c + a) c +b a b a c b c 1 9 ⇔ P ≤ + + + + + = + + =
a + b b + a (a + c) (c + a) 1 1 . 4 4
b + c b + c 4 4
Dấu “=” xảy ra khi và chỉ khi: a a =
a +b 4(a + c)
a + b = 4(a + c) b b a = c a = c b = ⇔ b
+ c = b + a ⇔ ⇔ ⇔ a = c = .
b + c b + a
a + b = 4.2a b = 7a 7
4(c + a) = c + b c c =
4(c + a) c + b
Vậy giá trị lớn nhất của P là 9 khi b a = c = . 4 7
_____ THCS.TOANMATH.com _____
Document Outline
- de-tuyen-sinh-lop-10-thpt-mon-toan-nam-2022-2023-so-gddt-lang-son
- 36. LẠNG SƠN