Lời giải đề toán vào lớp 10 tỉnh Lào Cai 2022 Điện thoại: 0866855096 Pytago EDUCATION LỜI GIẢI THAM KHẢO 1 Noi dung van
ĐỀ TOÁN (CHUNG) KỲ THI TUYỂN SINH VÀO LỚP 10 TỈNH LÀO CAI NĂM HỌC 2022 - 2023
Câu 1 (1,0 điểm). Tính giá trị các biểu thức sau: √ √ √ a) 2 + 36. b) 25 − 9. Lời giải. √ a) 2 + 36 = 2 + 6 = 8. √ √ b) 25 − 9 = 5 − 3 = 2. √ Å 1 1 ã x
Câu 2 (1,5 điểm). Cho biểu thức P = √ + √ : √ (với x > 0, x 6= 1). x + 1 x − 1 x − 1
a) Rút gọn biểu thức P . 1
b) Tìm giá trị của x để P = . 2 Lời giải.
a) Với điều kiện x > 0, x 6= 1 ta có √ Å 1 1 ã x P = √ + √ : √ x + 1 x − 1 x − 1 √ √ √ x − 1 + x + 1 x − 1 = √ √ · √ ( x + 1)( x − 1) x √ √ 2 x x − 1 1 = √ √ · √ ( x + 1)( x − 1) x 2 = √ . x + 1 1 2 1 √ √ b) Để P = ⇔ √ = ⇔ x + 1 = 4 ⇔
x = 3 ⇔ x = 9 (thỏa mãn điều kiện). 2 x + 1 2 Vậy x = 9. Câu 3 (2,5 điểm).
a) Giải phương trình: x2 + 2x − 8 = 0.
b) Tìm các giá trị của tham số k để đường thẳng d1 : y = (k − 1) x + k song song với đường thẳng d2 : y = 3x − 12.
Z Trung tâm toán học Pytago 1
Đ/c: 095 Kim Sơn, 273 Trần Hưng Đạo
Lời giải đề toán vào lớp 10 tỉnh Lào Cai 2022 Điện thoại: 0866855096
c) Tìm các giá trị của tham số m để đường thẳng d : y = −x + m + 1 cắt Parabol (P ) : y = x2
tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn điều kiện: x2 − x 1 2 − 4m + 1 = 0. Lời giải.
a) Giải phương trình: x2 + 2x − 8 = 0.
Ta có: ∆0 = 12 − 1 · (−8) = 9 > 0
Phương trình có 2 nghiệm phân biệt √ −1 + 9 −1 + 3 x1 = = = 2 1 √ 1 −1 − 9 −1 − 3 x2 = = = −4. 1 1 b) d1 : y = (k − 1) x + k d2 : y = 3x − 12.   k − 1 = 3 k = 4 Để d1 k d2 ⇔ ⇔ ⇔ k = 4. k 6= −12 k 6= −12 Vậy k = 4. c) d : y = −x + m + 1 (P ) : y = x2.
Xét phương trình hoành độ giao điểm của d và (P ) : x2 = −x + m + 1 ⇔ x2 + x − m − 1 = 0. (1)
∆ = 12 − 4 (−m − 1) = 4m + 5. 5
Để d cắt (P ) tại 2 điểm phân biệt có hoành độ x1, x2 ⇔ ∆ > 0 ⇔ m > − (2) 4  x1 + x2 = −1 Áp dụng định lý Vi-et: .  x1 · x2 = −m − 1
Vì x1 là nghiệm của phương trình (1) nên x2 + x = −x 1 1 − m − 1 = 0 ⇔ x2 1 1 + m + 1 Ta có: x2 − x 1 2 − 4m + 1 = 0
⇔ −x1 + m + 1 − x2 − 4m + 1 = 0
⇔ − (x1 + x2) − 3m + 2 = 0 ⇔ − (−1) − 3m + 2 = 0 ⇔ −3m + 3 = 0 ⇔ m = 1 (thỏa mãn (2)). Vậy m = 1. Câu 4 (1,5 điểm).  x + y = −1
a) Giải hệ phương trình: 2x − y = 4.
b) Hai ô tô xuất phát cùng một thời điểm từ địa điểm A đến địa điểm B với vận tốc mỗi ô tô
không đổi. Sau 1 giờ quãng đường đi được của ô tô thứ nhất nhiều hơn quãng đường đi được
Z Trung tâm toán học Pytago 2
Đ/c: 095 Kim Sơn, 273 Trần Hưng Đạo
Lời giải đề toán vào lớp 10 tỉnh Lào Cai 2022 Điện thoại: 0866855096
của ô tô thứ hai là 5km. Quãng đường đi được của ô tô thứ hai sau 3 giờ nhiều hơn quãng
đường đi được của ô tô thứ nhất sau 2 giờ là 35km. Tính vận tốc mỗi ô tô. Lời giải.    x + y = −1 3x = 3 x = 1 a) ⇔ ⇔ 2x − y = 4 x + y = −1 y = −2.
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (1; −2) .
b) Gọi vận tốc của ô tô thứ nhất và ô tô thứ hai lần lượt là x (km/h), y (km/h) (x > 0; y > 0).
Sau 1 giờ quãng đường đi được của ô tô thứ nhất nhiều hơn quãng đường đi được của ô tô
thứ hai là 5km nên có phương trình x − y = 5 (1).
Quãng đường đi được của ô tô thứ hai sau 3 giờ nhiều hơn quãng đường đi được của ô tô thứ
nhất sau 2 giờ là 35km nên có phương trình
3y − 2x = 35 ⇔ −2x + 3y = 35 (2).
Từ (1) và (2) ta được hệ phương trình    x − y = 5 2x − 2y = 10 x = 50 (TMĐK) ⇔ ⇔  − 2x + 3y = 35  − 2x + 3y = 35 y = 45 (TMĐK).
Vậy vận tốc của ô tô thứ nhất là 50km/h; vận tốc của ô tô thứ hai là 45km/h.
Câu 5 (0,5 điểm). Chọn ngẫu nhiên một số trong các số tự nhiên từ 1 đến 10. Tính xác suất
để số được chọn là số chia hết cho 5. Lời giải.
Không gian mẫu của phép thử là Ω = {1; 2; . . . ; 10}. Suy ra n(Ω) = 10.
Gọi A là biến cố: “ Số được chọn chia hết cho 5 ”.
Ta có A = {5; 10} ⇒ n(A) = 2. n(A) 2 1
Vậy xác suất của biến cố A là P (A) = = = . n(Ω) 10 5
Câu 6 (1,0 điểm). Cho tam giác ABC vuông tại A, độ dài các cạnh góc vuông: AB = 1, √ AC = 3. a) Tính độ dài cạnh BC. √6
b) Trên tia đối của tia BC lấy điểm M sao cho AM = . Tính số đo góc ÷ AM C. 2 Lời giải.
Z Trung tâm toán học Pytago 3
Đ/c: 095 Kim Sơn, 273 Trần Hưng Đạo
Lời giải đề toán vào lớp 10 tỉnh Lào Cai 2022 Điện thoại: 0866855096 A √6 √ 2 1 3 M B H C
a) Áp dụng định lý Pytago cho 4ABC vuông tại A ta có √
BC2 = AB2 + AC2 = 12 + ( 3)2 = 4. ⇒ BC = 2.
b) Kẻ đường cao AH của 4ABC
Áp dụng hệ thức lượng trong 4ABC vuông tại A, đường cao AH ta được AH · BC = AB · AC √ √ AB · AC 1 · 3 3 ⇒ AH = = = . BC 2 2 Xét 4AHM , ta có: √ √ √ AH 3 6 2 sin ÷ AM H = = : = AM 2 2 2 ⇒ ÷ AM H = 45◦. Vậy ÷ AM C = 45◦.
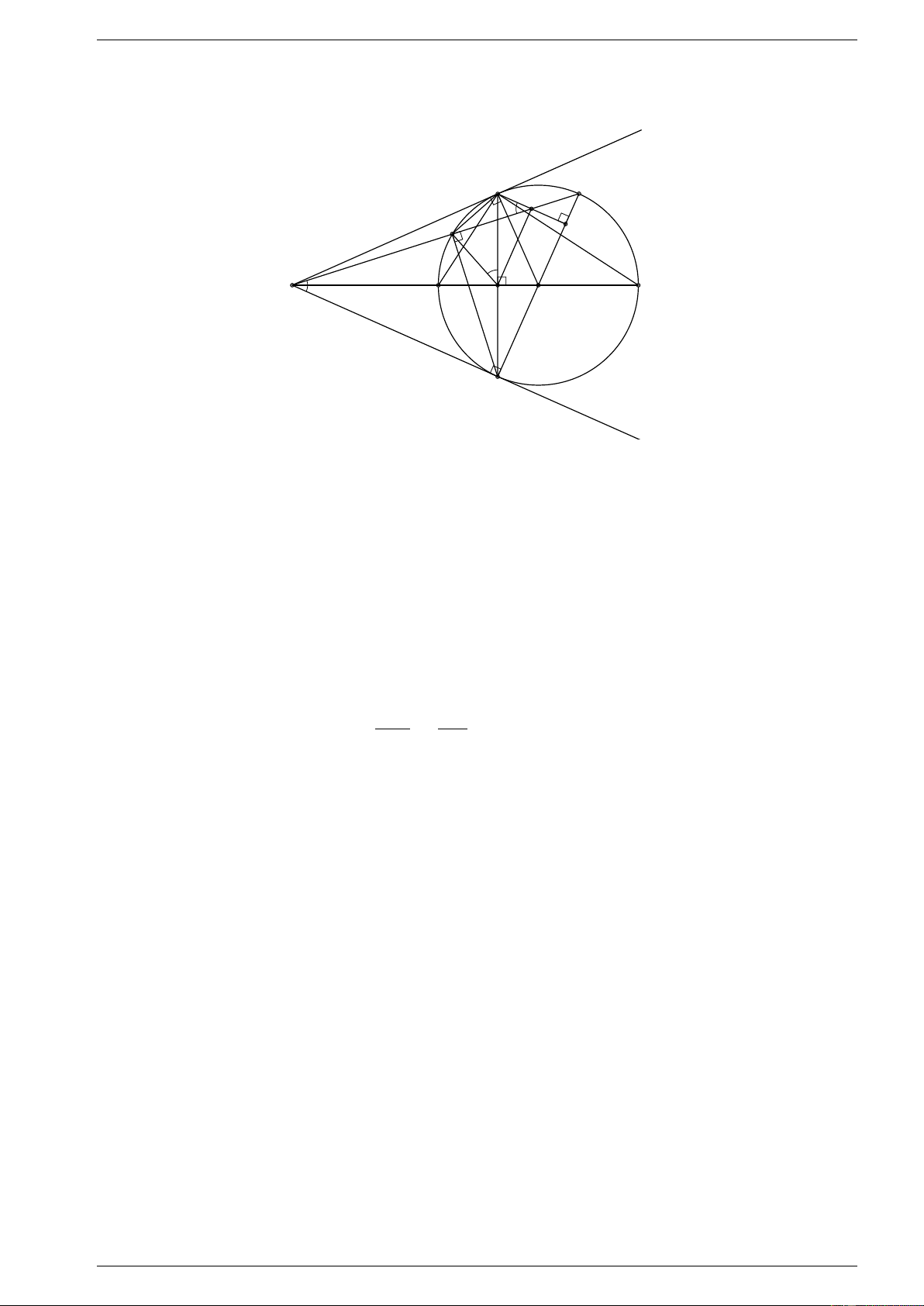
Câu 7 (2,0 điểm). Cho đường tròn (O) và điểm M ngoài đường tròn. Qua M kẻ hai tiếp tuyến
phân biệt M A, M B đến đường tròn (A, B là các tiếp điểm).
a) Chứng minh M AOB là tứ giác nội tiếp.
b) Đường thẳng M O cắt đường tròn (O) lần lượt tại hai điểm C, D phân biệt sao cho M C < M D.
Chứng minh: M A · DA = M D · AC
c) Đường thẳng BO cắt đường tròn (O) tại điểm thứ hai là E. Kẻ AI vuông góc với BE tại
I. Đường thẳng M E cắt AI tại K, đường thẳng M O cắt AB tại H. Chứng minh hai đường thẳng HK và BE song song. Lời giải.
Z Trung tâm toán học Pytago 4
Đ/c: 095 Kim Sơn, 273 Trần Hưng Đạo
Lời giải đề toán vào lớp 10 tỉnh Lào Cai 2022 Điện thoại: 0866855096 A E K F I C D M H O B
a) Vì M A, M B là hai tiếp tuyến của (O) ⇒ ÷ M AO = ÷ M BO = 90◦. ⇒ ÷ M AO + ÷ M BO = 180◦
mà hai góc này ở vị trí đối nhau
⇒ M AOB là tứ giác nội tiếp.
b) Xét tam giác M AC và tam giác M DA có:  ÷ AM D chung; ÷ M AC = ÷
M DA ( góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung cùng chắn cung ˜ AC) M A AC ⇒ 4M AC v 4MDA (g.g) ⇒ = ⇒ M A · AD = M D · AC. M D AD c) Cách 1:
Gọi F là giao điểm thứ hai của M E với (O).  AI ⊥ BE ; Ta có: ⇒ AI k M B ⇒ ÷ AKM = ÷ F M B (hai góc so le trong) (1) M B ⊥ BE 
M A = M B (tính chất hai tiếp tuyến); Ta có:
⇒ M O là đường trung trực của AB OA = OB(= R) ⇒ ÷ M HB = 90◦ (2). Ta có: ’
BF E = 90◦ (góc nội tiếp chắn nửa đường tròn) ⇒ ÷ M F B = 90◦ (3) Từ (2),(3) ⇒ ÷ M F B = ÷
M HB = 90◦ mà hai góc này cùng nhìn M B
⇒ Tứ giác M BHF là tứ giác nội tiếp. ⇒ ÷ F M B = ’ F HA (4) Từ (1), (4) ⇒ ’ F HA = ’
AKF mà hai góc này cùng nhìn AF
⇒ Tứ giác AF HK nội tiếp đường tròn. ⇒ ’ AF K = ’ AHK.
Z Trung tâm toán học Pytago 5
Đ/c: 095 Kim Sơn, 273 Trần Hưng Đạo
Lời giải đề toán vào lớp 10 tỉnh Lào Cai 2022 Điện thoại: 0866855096 Mặt khác ’ AF E = ’
ABE (hai góc nội tiếp cùng chắn ˜ AE). ⇒ ’ AHK = ’
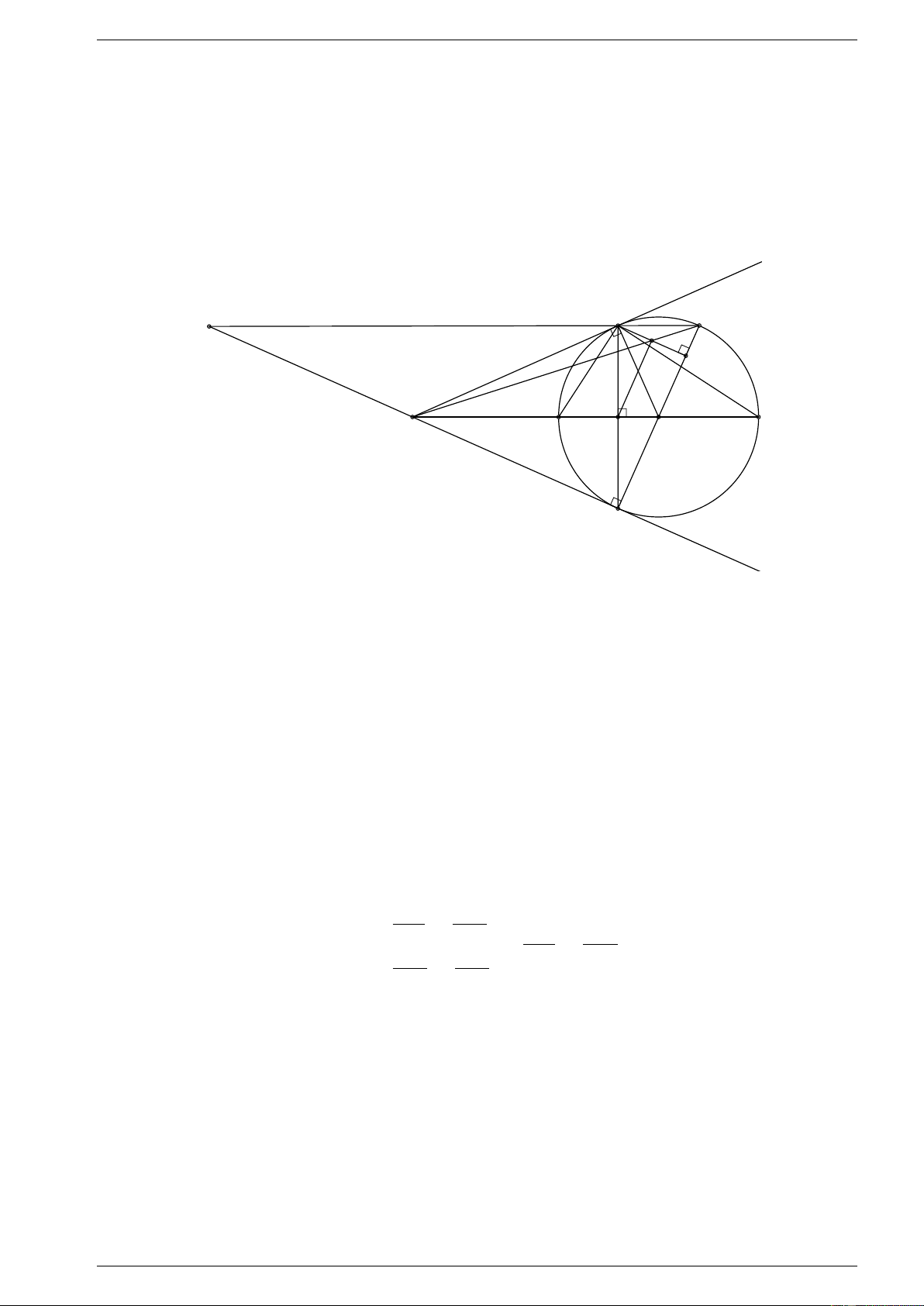
ABE mà hai góc này ở vị trí đồng vị ⇒ HK k BE. Cách 2: A E S K I C D M H O B Gọi S = AE ∩ M B.
Vì M A = M B (tính chất hai tiếp tuyến cắt nhau) ⇒ 4M AB cân tại M . ⇒ ÷ M AB = ÷ M BA (1) Do ’
BAE = 90◦ (góc nội tiếp chắn nửa đường tròn)⇒ ’ SAB = 90◦. Lại có ’ ASM + ÷ M BA = 90◦ (2) ’ SAM + ÷ M AB = 90◦ (3) Từ (1),(2),(3) ⇒ ’ M SA = ’
M AS ⇒ 4M SA cân tại M ⇒ M A = M S Suy ra M B = M S.  M B ⊥ BE ; Do ⇒ AI k SB. AI ⊥ BE  AK EK  =  AK KI
Áp dụng định lý Ta - let ta có: SM EM ⇒ = KI EK SM M B   = M B EM mà SM = M B.
Suy ra AK = KI ⇒ K là trung điểm của AI (*).
Chứng minh tương tự cách 1 ta có OM là đường trung trực của AB
⇒ H là trung điểm của AB.
⇒ HK là đường trung bình của 4ABI ⇒ HK k BE.
Z Trung tâm toán học Pytago 6
Đ/c: 095 Kim Sơn, 273 Trần Hưng Đạo
Document Outline

• Doc1
• dethithuvao10_chinhthuc_2022