Đề tuyển sinh lớp 10 THPT môn Toán năm 2022 – 2023 sở GD&ĐT Nghệ An
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi chính thức kỳ thi tuyển sinh vào lớp 10 THPT môn Toán năm học 2022 – 2023 sở Giáo dục và Đào tạo tỉnh Nghệ An; đề thi gồm 01 trang với 05 bài toán dạng tự luận, thời gian học sinh làm bài thi là 120 phút (không kể thời gian giám thị phát đề); kỳ thi được diễn ra vào thứ Tư ngày 08 tháng 06 năm 2022. Mời các bạn đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
1
LỜI GIẢI ĐỀ THI TUYỂN SINH VÀO LỚP 10 TỈNH NGHỆ AN
Được thực hiện bởi Nguyễn Nhất Huy, thầy Trịnh Văn Luân Bài 1: √ √ √ a) Tính A = 81 − 36 + 49. √ 1 1 x − x
b) Rút gọn biểu thức P = √ − √ · , với x > 0 và x ̸= 1. x − 1 x 2022
c) Xác định hệ số a, b của hàm số y = ax + b, biết đồ thị của hàm số đi qua điểm M (−1; 3)
và cắt trục tung tại điểm có tung độ bằng −2. Hướng dẫn giải √ √ √ a) Ta có A = 92 − 62 + 72 = 9 − 6 + 7 = 10.
b) Với x > 0 và x ̸= 1, ta có: √ 1 1 x − x P = √ − √ · x − 1 x 2022 √ √ √ √ x − x + 1 x( x − 1) = √ √ · x( x − 1) 2022 √ √ 1 x( x − 1) = √ √ · x( x − 1) 2022 1 = . 2022
c) Do đồ thị hàm số y = ax + b đi qua điểm M (−1; 3) nên 3 = −a + b ⇔ −a + b = 3 (1).
Đồ thị hàm số y = ax + b cắt trục tung tại điểm có tung độ bằng −2, tức là đồ thị hàm
số đi qua điểm B(0; −2).
Suy ra −2 = a · 0 + b ⇔ b = −2.
Thay vào (1) ta được −a − 2 = 3 ⇔ a = −5. Vậy a = −5; b = −2. Bài 2:
a) Giải phương trình 2x2 − 9x + 10 = 0.
b) Cho phương trình x2 + 3x − 1 = 0 có hai nghiệm phân biệt x1, x2. Không giải phương 3|x1 − x2|
trình, hãy tính giá trị của biểu thức T = . x2x 1 2 + x1x2 2 Hướng dẫn giải
a) Ta có ∆ = (−9)2 − 4 · 2 · 10 = 1 > 0. Suy ra phương trình có hai nghiệm phân biệt 2 √ √ −(−9) + 1 5 −(−9) − 1 x1 = = .; x2 = = 2. 2 · 2 2 2 · 2 5
Vậy phương trình có hai nghiệm phân biệt x1 = ; x2 = 2. 2
b) Ta có ∆ = 32 − 4 · 1 · (−1) = 13 > 0, nên phương trình có hai nghiệm phân biệt. x1 + x2 = −3 Theo định lý Viét, ta có x1x2 = −1. Có (|x1 − x2|)2 = x2 − 2x = (x 1 1x2 + x2 2
1 + x2)2 − 4x1x2 = (−3)2 − 4(−1) = 13. √ Suy ra |x1 − x2| = 13. Và x2x = x 1 2 + x1x2 2
1x2(x1 + x2) = (−1) · (−3) = 3.. √ 3 13 √ Vậy T = = 13. 3 Bài 2:
Trong kỳ SEA Games 31 tổ chức tại Việt Nam, thú sao la được chọn làm linh vật. Một phân
xưởng được giao sản xuất 420 thú nhồi bông sao la trong một thời gian dự định để làm quà
tặng. Biết rằng nếu mỗi giờ phân xưởng sản xuất thêm 5 thú nhồi bông sao la thì sẽ rút ngắn
thời gian hoàn thành công việc là 2 giờ. Tính thời gian dự định của phân xưởng. Hướng dẫn giải
Gọi thời gian dự định sản xuất sao la nhồi bông của phân xưởng là x (giờ, x > 0). 420
Khi đó năng suất dự định của phân xưởng là (sản phẩm/ giờ). x
Thời gian thực tế của phân xưởng là x − 2 (giờ). 420
Năng suất thực tế của phân xưởng là (sản phẩm / giờ). x − 2
Do thực tế mỗi giờ phân xưởng sản xuất thêm 5 thú nhồi bông nên ta có phương trình 420 420 − = 5 x − 2 x 420x 420(x − 2) 5x(x − 2) ⇔ − = x(x − 2) x(x − 2) x(x − 2)
⇒ 420x − 420x + 840 = 5x2 − 10x ⇔ 5x2 − 10x − 840 = 0 ⇔ x2 − 2x − 168 = 0.
Ta có ∆′ = (−1)2 − 1 · (−168) = 169 > 0. Suy ra phương trình có hai nghiệm phân biệt.
x1 = 14 (thoả mãn); x2 = −12 (loại).
Vậy thời gian dự định của phân xưởng là 14 giờ. 3 Bài 4:
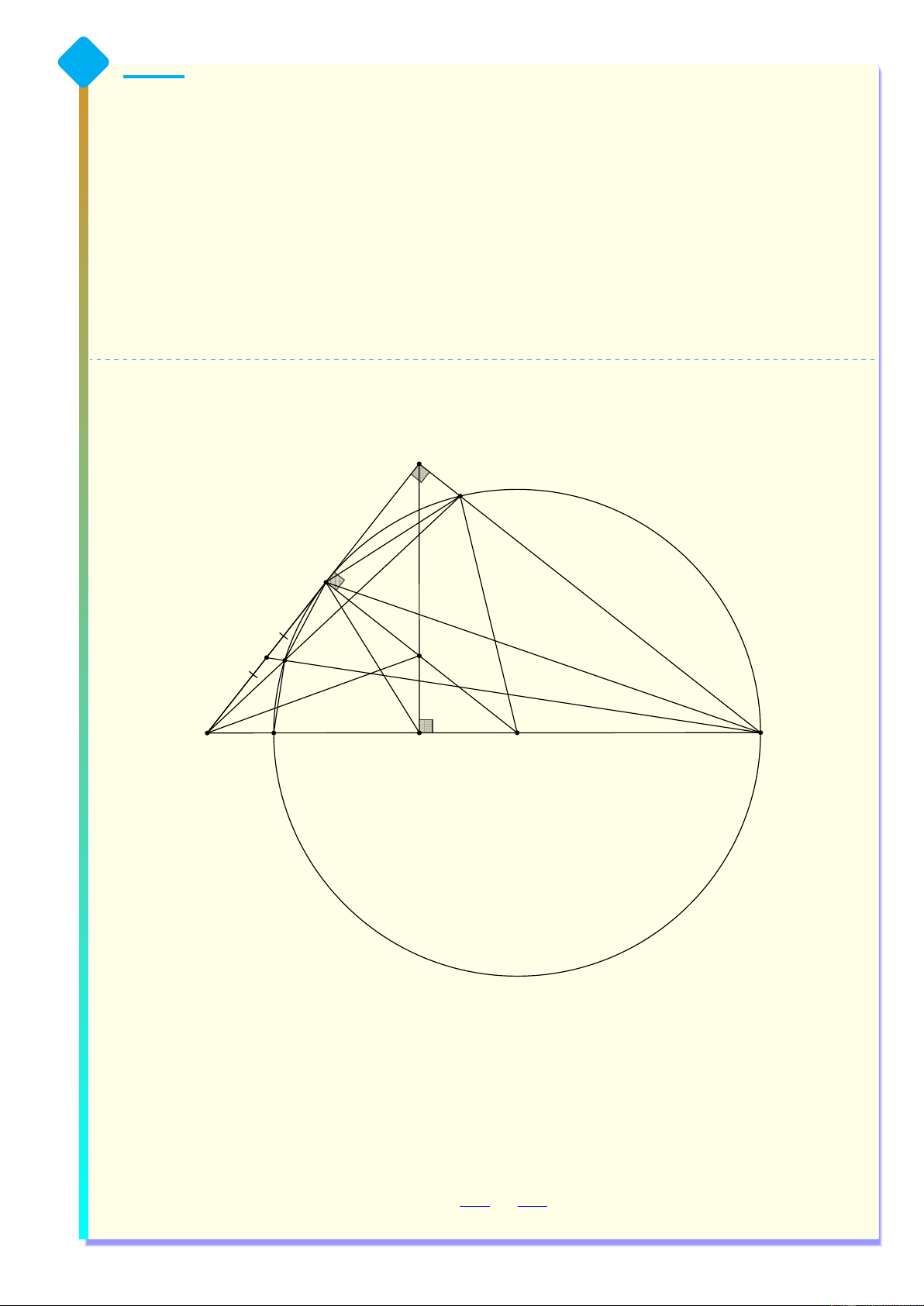
Cho tam giác ABC vuông tại C (AC < BC), đường cao CK và đường phân giác trong BD
(K ∈ AB, D ∈ AC). Qua D kẻ đường thẳng vuông góc với AC cắt CK, AB lần lượt tại H và I.
a) Chứng minh CDKI là tứ giác nội tiếp.
b) Chứng minh AD · AC = DH · AB.
c) Gọi F là trung điểm AD. Đường tròn tâm I bán kính ID cắt BC tại M (M khác B) và
cắt AM tại N (N khác M ). Chứng minh B, N, F thẳng hàng. Hướng dẫn giải C M D F F' H , N A B L K I
a) Theo giả thiết vì CK là đường cao và DI vuông góc AC nên ta có [ CDI = [ CKI = 90◦
Suy ra tứ giác CDKI là tứ giác nội tiếp.
b) Vì BD là phân giác nên theo tính chất đường phân giác ta có AD AB = . (1) DC BC 4 Vì [ CAB chung, \ AKC = [
ACB = 90◦. nên ∆ACK ∽ ∆ABC(g.g). Do đó ta được AB AC = . (2) BC CK
Từ (1) và (2) ta được tỷ lệ thức AD AB AC AC CK = = ⇔ = (3) DC BC CK AD CD
Vì CDKI là tứ giác nội tiếp nên \ ADK = [ AIC, [
CAI chung nên ∆ADK ∽ ∆AIC(g.g). Do đó ta được AD · AC = AK · AI. (4)
Vì DI, CB cùng vuông góc với AC nên DI ∥ CB. Theo định lý Thales ta được AB AC = . (5) AI AD Vì \ DCH chung, \ CDH = \
CKA = 90◦ nên ∆CDH ∽ ∆CKA(g.g). Do đó ta được AK CK = . (6) DH CD
Từ (3), (5) và (6) ta được AK AB = ⇔ AK · AI = DH · AB DH AI
Kết hợp với (4) ta được AD · AC = AK · AI = DH · AB.
Vậy bài toán được chứng minh. c) Ta có [ IDB = \ CBD = [
IBD(so le trong vì DI ∥ CB và BD là phân giác [ CBA).
Do đó ∆IBD cân tại I suy ra ID = IB hay B thuộc (I, ID).
Vì ID ⊥ AC nên AC là tiếp tuyến của (I, ID).
Gọi F ′ là giao của BN với AC, L là giao của (I, ID) với AB.
Vì F ′D là tiếp tuyến của (I, ID) (do AC là tiếp tuyến) nên F ′D2 = F ′N · F ′B. (*)
Vì tứ giác LN M B nội tiếp (I, ID) nên \ N LB = \
CM A mà theo giả thiết ta có \ M CA = \
BN L = 90◦ (vì BL là đường kính) nên ∆M CA ∽ ∆LNB(g.g) suy ra \ F ′BA = \ N BL = \ M AC = \ F ′AN Kết hợp với góc \
AF ′B chung ta được ∆AF ′N ∽ ∆BF ′A(g.g) do đó ta được tỷ lệ thức F ′N F ′A =
⇔ F ′A2 = F ′N · F ′B. (**) F ′A F ′B
Từ (∗) và (∗∗) ta suy ra F ′D = F ′A hay F ′ là trung điểm AD nên F ′ trùng F . Vậy B, N, F thẳng hàng. 5 Bài 5: √ 1 √ Giải phương trình x2 + 1 + 3 = − 3 9x2 − 6x + 2 + 3 (1). x Hướng dẫn giải Điều kiện x ̸= 0. √ Nhận thấy V T =
x2 + 1 + 3 > 0, với mọi x ̸= 0.
Khi đó để phương trình có nghiệm thì vế phải của (1) phải lớn hơn 0. 1 √ Hay − 3 9x2 − 6x + 2 + 3 > 0 x 1 ⇔ − p 3 > 0 do 1 (1 − 3x)2 + 1 + 3 > 0 ∀x ̸= 0 x 1 − 3x 1 ⇔ > 0 ⇔ 0 < x < . x 3 √ 1 √ Ta có x2 + 1 + 3 = − 3 9x2 − 6x + 2 + 3 x √ ⇔ p x x2 + 1 + 3x = (1 − 3x) (1 − 3x)2 + 1 + 3 √ ⇔ p x x2 + 1 + 3 = (1 − 3x) (1 − 3x)2 + 1 + 3 .
Đặt 1 − 3x = t (điều kiện t > 0). √ √
Khi đó phương trình trở thành: x x2 + 1 + 3 = t t2 + 1 + 3 √ √ ⇔ x4 + x2 − t4 + t2 + 3 · (x − t) = 0 √ √ √ √ ( x4 + x2 − t4 + t2)( x4 + x2 + t4 + t2) ⇔ √ √ + 3(x − t) = 0 x4 + x2 + t4 + t2 (x4 − t4) + (x2 − t2) ⇔ √ √ + 3(x − t) = 0 x4 + x2 t4 + t2)
(x − t)(x + t)(x2 + t2) + (x − t)(x + t) ⇔ √ √ + 3(x − t) = 0 x4 + x2 + t4 + t2 (x + t)(x2 + t2 + 1) ⇔ (x − t) √ √ + 3 = 0. x4 + x2 + t4 + t2 (x + t)(x2 + t2 + 1) ⇔ x − t = 0 do √ √ + 3 > 0 x4 + x2 + t4 + t2 ⇔ x = t. 1 Suy ra x = 1 − 3x ⇔ x = (thoả mãn). 4 1
Vậy phương trình có nghiệm duy nhất x = . 4
Document Outline
- de-tuyen-sinh-lop-10-thpt-mon-toan-nam-2022-2023-so-gddt-nghe-an
- Lời giải đề thi vào 10 Tỉnh Nghệ An 2022