Đề tuyển sinh lớp 10 THPT môn Toán năm 2024 – 2025 sở GD&ĐT Cao Bằng

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề chính thức kỳ thi tuyển sinh vào lớp 10 Trung học Phổ thông môn Toán năm học 2024 – 2025 sở Giáo dục và Đào tạo tỉnh Cao Bằng; đề thi có đáp án và lời giải chi tiết. Mời bạn đọc đón xem!

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

5 trang 1 tháng trước

Tác giả:

Profile Lê Phương
TUYỂN TẬP ĐỀ TUYỂN SINH VÀO 10 – NĂM 2024-2025
SẢN PHẨM CỦA NHÓM: WORD-GIẢI-TÁCH CHUYÊN ĐỀ VÀO 10 CÁC TỈNH Trang 1
SỞ GIÁO DỤC ĐÀO TẠO
CAO BẰNG
KỲ THI TUYỂN SINH LỚP 10
NĂM HỌC: 2024 – 2025
Môn: TOÁN (chung)
Khoá thi ngày: 06/06/2024
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Câu 1. (4,0 điểm)
a) Thực hiện phép tính:
5 16
3−
.
b) Cho hàm số
2
y ax
=
( )
0a ≠
. Tìm giá trị của
a
để
thì
12
y
=
.
c) Giải phương trình sau:
2
6 70xx+ −=
.
d) Giải hệ phương trình:
35
24
xy
xy
+=−
−=
.
Câu 2. (1,0 điểm)
Bạn Hưng đi xe đạp từ nhà đến trường với quãng đường
10
km. Khi đi từ trường về nhà, vẫn trên
cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Hưng phải giảm vận tốc
2
km/h so với
khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là
10
phút. Tính vận tốc của xe đạp
khi bạn Hưng đi từ nhà đến trường và từ trường về nhà.
Câu 3. (1,0 điểm)
Cho tam giác
ABC
vuông tại
A
có các cạnh
6
AB =
cm;
10BC =
cm.
a) Tính độ dài đoạn thẳng
AC
.
b) Kẻ đường cao
AH
. Tính độ dài đoạn thẳng
AH
.
Câu 4. (2,0 điểm)
Cho tam giác
ABC
nhọn nội tiếp đường tròn
( )
O
. Hai đường cao
BM
,
CN
cắt nhau tại
H
(
M AC∈
,
)
N AB∈
.
a) Chứng minh
AMHN
là tứ giác nội tiếp.
b) Chứng minh
..AN BC AC MN=
và
OA MN
⊥
.
Câu 5. (1,0 điểm)
Cho phương trình
( )
22
2 1 20x m xm− + + +=
(
m
là tham số). Tìm cả các giá trị nguyên của
m
để
phương trình đã cho có hai nghiệm phân biệt
1
x
và
2
x
sao cho biểu thức
12
12
xx
P
xx
=
+
có giá trị nguyên.
--------------------------------- Hết ---------------------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
ĐỀ CHÍNH THỨC
TUYỂN TẬP ĐỀ TUYỂN SINH VÀO 10 – NĂM 2024-2025
SẢN PHẨM CỦA NHÓM: WORD-GIẢI-TÁCH CHUYÊN ĐỀ VÀO 10 CÁC TỈNH Trang 2
HƯỚNG DẪN GIẢI
Câu 1. (4,0 điểm)
a) Thực hiện phép tính:
5 16 3−
.
b) Cho hàm số
2
y ax=
(
)
0a ≠
. Tìm giá trị của
a
để
thì
12
y =
.
c) Giải phương trình sau:
2
6 70xx+ −=
.
d) Giải hệ phương trình:
35
24
xy
xy
+=−
−=
.
Lời giải
a) Thực hiện phép tính:
5 3 5.4 3 20 3 1716 −= −= −=
b) Cho hàm số
2
y ax=
(
)
0a ≠
. Tìm giá trị của
a
để
2x =
thì
12
y =
Thay
2
x =
và
12y
=
vào hàm số
2
y ax=
( )
0a ≠
ta được:
2
12 .2 3aa= ⇒=
(thoã mãn)
Vậy
3
a =
c) Giải phương trình sau:
2
6 70xx+ −=
.
Ta có
0
abc++=
nên phương trình có hai nghiệm phân biệt
1
1x =
và
2
7
c
x
a
= = −
Vậy phương trình có tập nghiệm là
{
}
1; 7S = −
.
d) Giải hệ phương trình:
35 35 77 1
2 4 6 3 12 3 5 2
xy xy x x
xy x y x y y
+=− +=− = =
 
⇔ ⇔⇔
 
−= − = + =− =−
 
Vậy hệ phương trình đã cho có nghiệm duy nhất
1
2
x
y
=
= −
.
Câu 2. (1,0 điểm)
Bạn Hưng đi xe đạp từ nhà đến trường với quãng đường
10
km. Khi đi từ trường về nhà, vẫn trên
cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Hưng phải giảm vận tốc
2
km/h so với
khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là
10
phút. Tính vận tốc của xe đạp
khi bạn Hưng đi từ nhà đến trường và từ trường về nhà
Lời giải
Gọi
x
(km/h) là vận tốc đi xe từ nhà đến trường của Hưng
( 2)x >
Vận tốc khi về là:
2
x −
(km/h)
Thời gian đi là:
10
x
(h)
Thời gian về là:
10
2x −
(h)
Vì thời gian về nhà nhiều hơn thời gian đến trường là
10
phút
1
6
=
giờ nên ta có :
2
2
10 10 1
26
10.6 10.6( 2) ( 2)
6 ( 2) 6 ( 2) 6 ( 2)
60 60 120 2
2 120 0
( 12)( 10) 0
12( )
10( )
xx
xxx
xx xx xx
xx xx
xx
xx
x tm
x loai
−=
−
−−
⇔− =
−−−
⇔−+=−
⇔−− =
⇔− + =
=
⇔
= −
Vậy vận tốc khi đi là:
12( / )km h
, vận tốc khi đi là:
12 2 10( / )km h−=
TUYỂN TẬP ĐỀ TUYỂN SINH VÀO 10 – NĂM 2024-2025
SẢN PHẨM CỦA NHÓM: WORD-GIẢI-TÁCH CHUYÊN ĐỀ VÀO 10 CÁC TỈNH Trang 3
Câu 3. (1,0 điểm)
Cho tam giác
ABC
vuông tại
A
có các cạnh
6AB =
cm;
10BC =
cm.
a) Tính độ dài đoạn thẳng
AC
.
b) Kẻ đường cao
AH
. Tính độ dài đoạn thẳng
AH
.
Lời giải
a) Áp dụng định lí Pytago trong tam giác vuông
ABC
, ta có:
222
AB AC BC
+=
hay
2 22
6 10AC+=
.
2 22
10 6 64AC⇒ = −=
.
8
AC⇒=
(cm).
Vậy
8AC =
cm.
b) Xét tam giác
ABC
vuông tại
A
, đường cao
AH
có:
..AH BC AB AC=
.10 6.8AH⇒=
6.8 24
4,8
10 5
AH⇒===
(cm).
Vậy
4,8AH =
cm.
Câu 4. (2,0 điểm)
Cho tam giác
ABC
nhọn nội tiếp đường tròn
( )
O
. Hai đường cao
BM
,
CN
cắt nhau tại
H
(
M AC∈
,
)
N AB∈
.
a) Chứng minh
AMHN
là tứ giác nội tiếp.
b) Chứng minh
..AN BC AC MN=
và
OA MN⊥
.
Lời giải
a) Do
BM
,
CN
là đường cao nên
90ANH AMH= = °
.
Xét tứ giác
AMHN
có
90 90 180ANH AMH+ = °+ °= °
.
Mà hai góc này ở vị trí đối diện nên tứ giác
AMHN
là tứ giác nội tiếp.
b) Ta có
BM
,
CN
là đường cao nên
90ANH AMH= = °
.
⇒
B
,
M
,
N
,
C
cùng thuộc đường tròn đường kính
BC
.
TUYỂN TẬP ĐỀ TUYỂN SINH VÀO 10 – NĂM 2024-2025
SẢN PHẨM CỦA NHÓM: WORD-GIẢI-TÁCH CHUYÊN ĐỀ VÀO 10 CÁC TỈNH Trang 4
⇒
AMN ABC
=
(góc ngoài của đỉnh đối diện tứ giác nội tiếp).
Xét
AMN
∆
và
ABC∆
có:
( )
cmt
chung
AMN ABC
BAC
=
⇒
AMN ABC∆∆
(g.g)
⇒
MN AN
BC AC
=
⇒
..AN BC MN AC=
.
Kẻ tiếp tuyến
Ax
của
(
)
O
tại
A
. Khi đó
Ax OA⊥
CAx ABC=
(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn
AC
).
( )
cmtABC AMN
=
⇒
CAx AMN=
⇒
//
Ax MN
.
Mà
Ax OA
⊥
⇒
MN OA⊥
(đpcm).
Câu 5. (1,0 điểm)
Cho phương trình
( )
22
2 1 20x m xm− + + +=
(
m
là tham số). Tìm cả các giá trị nguyên của
m
để
phương trình đã cho có hai nghiệm phân biệt
1
x
và
2
x
sao cho biểu thức
12
12
xx
P
xx
=
+
có giá trị nguyên.
Lời giải
Ta có
( )
( )
2
22 2
214 24 414 847m m mm m m∆= + − + = + + − − = −
Để phương trình có hai nghiệm phân biệt
12
,
xx
0⇔∆>
4 70m⇔ −>
7
4
m⇔>
Áp dụng định lý Vi -ét
12
2
12
21
2
xx m
xx m
+= +
= +
Khi đó :
2 22
12
12
2 4 8 4 19 9
4 21
21 21 21 21
xx
m mm
PP m
xx m m m m
+ + −+
= = ⇒ = = = −+
++ + + +
4P
nguyên khi và chỉ khi
9
21m +
nguyên hay
92 1
m +
hay
{ }
2 1 U(9)= 1; 3; 9m +∈ ± ± ±
Ta có bảng sau
21
m +
9−
3−
1−
1
3
9
m
5( )L−
2( )L−
1( )L−
0( )L
1( )L
4( )TM
Với
4
m
=
thì
2
42
2( )
2.4 1
P tm
+
= =
+
Vậy
4
m =
thì phương trình đã cho có hai nghiệm phân biệt
12
,xx
sao cho biểu thức
12
12
xx
P
xx
=
+
có
giá trị nguyên.
--------------------------------- Hết ---------------------------------
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TUYỂN TẬP ĐỀ TUYỂN SINH VÀO 10 – NĂM 2024-2025
SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 CAO BẰNG
NĂM HỌC: 2024 – 2025
Môn: TOÁN (chung)
Khoá thi ngày: 06/06/2024 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Câu 1. (4,0 điểm)
a) Thực hiện phép tính: 5 16 − 3. b) Cho hàm số 2
y = ax (a ≠ 0). Tìm giá trị của a để x = 2 thì y =12.
c) Giải phương trình sau: 2
x + 6x − 7 = 0 . x + 3y = 5 −
d) Giải hệ phương trình:  . 2x − y = 4
Câu 2. (1,0 điểm)
Bạn Hưng đi xe đạp từ nhà đến trường với quãng đường 10km. Khi đi từ trường về nhà, vẫn trên
cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Hưng phải giảm vận tốc 2 km/h so với
khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là 10 phút. Tính vận tốc của xe đạp
khi bạn Hưng đi từ nhà đến trường và từ trường về nhà.
Câu 3. (1,0 điểm)
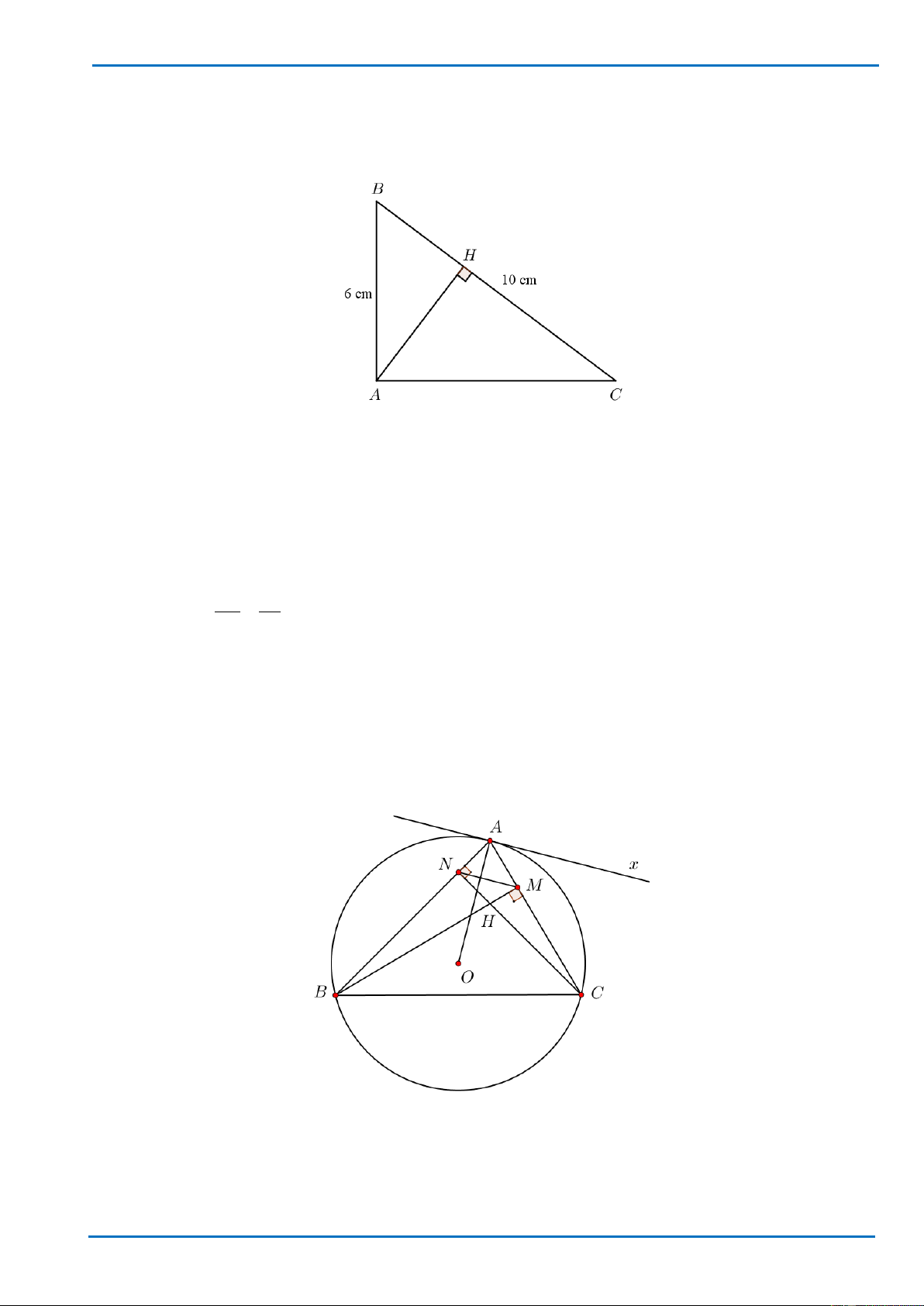
Cho tam giác ABC vuông tại A có các cạnh AB = 6cm; BC =10 cm.
a) Tính độ dài đoạn thẳng AC .
b) Kẻ đường cao AH . Tính độ dài đoạn thẳng AH .
Câu 4. (2,0 điểm)
Cho tam giác ABC nhọn nội tiếp đường tròn (O) . Hai đường cao BM , CN cắt nhau tại H
(M ∈ AC , N ∈ AB) .
a) Chứng minh AMHN là tứ giác nội tiếp.
b) Chứng minh AN.BC = AC.MN và OA ⊥ MN .
Câu 5. (1,0 điểm) Cho phương trình 2 x − ( m + ) 2 2
1 x + m + 2 = 0 ( m là tham số). Tìm cả các giá trị nguyên của m để
phương trình đã cho có hai nghiệm phân biệt x và x sao cho biểu thức x x 1 2 = có giá trị nguyên. 1 2 P x + x 1 2
--------------------------------- Hết ---------------------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
SẢN PHẨM CỦA NHÓM: WORD-GIẢI-TÁCH CHUYÊN ĐỀ VÀO 10 CÁC TỈNH  Trang 1 
TUYỂN TẬP ĐỀ TUYỂN SINH VÀO 10 – NĂM 2024-2025 HƯỚNG DẪN GIẢI
Câu 1. (4,0 điểm)
a) Thực hiện phép tính: 5 16 − 3. b) Cho hàm số 2
y = ax (a ≠ 0). Tìm giá trị của a để x = 2 thì y =12.
c) Giải phương trình sau: 2
x + 6x − 7 = 0 . x + 3y = 5 −
d) Giải hệ phương trình:  . 2x − y = 4 Lời giải
a) Thực hiện phép tính: 5 16 − 3 = 5.4 − 3 = 20 − 3 =17 b) Cho hàm số 2
y = ax (a ≠ 0). Tìm giá trị của a để x = 2 thì y =12
Thay x = 2 và y =12 vào hàm số 2
y = ax (a ≠ 0) ta được: 2 12 = .2 a ⇒ a = 3 (thoã mãn) Vậy a = 3
c) Giải phương trình sau: 2
x + 6x − 7 = 0 . Ta có a c
+ b + c = 0 nên phương trình có hai nghiệm phân biệt x =1 x = = 7 − 1 và 2 a
Vậy phương trình có tập nghiệm là S = {1;− } 7 . x + 3y = 5 − x + 3y = 5 − 7x = 7 x =1
d) Giải hệ phương trình:  ⇔  ⇔  ⇔ 2x y 4 6x 3y 12 x 3y 5  − = − = + = − y = 2 − x =1
Vậy hệ phương trình đã cho có nghiệm duy nhất  . y = 2 −
Câu 2. (1,0 điểm)
Bạn Hưng đi xe đạp từ nhà đến trường với quãng đường 10km. Khi đi từ trường về nhà, vẫn trên
cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Hưng phải giảm vận tốc 2 km/h so với
khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là 10 phút. Tính vận tốc của xe đạp
khi bạn Hưng đi từ nhà đến trường và từ trường về nhà Lời giải
Gọi x (km/h) là vận tốc đi xe từ nhà đến trường của Hưng (x > 2)
Vận tốc khi về là: x − 2 (km/h) 10 Thời gian đi là: (h) x10 Thời gian về là: (h) x − 2 1
Vì thời gian về nhà nhiều hơn thời gian đến trường là 10 phút = giờ nên ta có : 6 10 10 1 − = x − 2 x 6 10.6x 10.6(x − 2) (x − 2) ⇔ − =
6x(x − 2) 6x(x − 2) 6x(x − 2) 2
⇔ 60x − 60x +120 = x − 2x 2
⇔ x − 2x −120 = 0
⇔ (x −12)(x +10) = 0 x =12(tm) ⇔ x = 10( − loai)
Vậy vận tốc khi đi là: 12(km / h) , vận tốc khi đi là: 12 − 2 =10(km / h)
SẢN PHẨM CỦA NHÓM: WORD-GIẢI-TÁCH CHUYÊN ĐỀ VÀO 10 CÁC TỈNH  Trang 2 
TUYỂN TẬP ĐỀ TUYỂN SINH VÀO 10 – NĂM 2024-2025
Câu 3. (1,0 điểm)
Cho tam giác ABC vuông tại A có các cạnh AB = 6cm; BC =10 cm.
a) Tính độ dài đoạn thẳng AC .
b) Kẻ đường cao AH . Tính độ dài đoạn thẳng AH . Lời giải
a) Áp dụng định lí Pytago trong tam giác vuông ABC , ta có: 2 2 2
AB + AC = BC hay 2 2 2 6 + AC =10 . 2 2 2
⇒ AC =10 − 6 = 64 . ⇒ AC = 8 (cm). Vậy AC = 8 cm.
b) Xét tam giác ABC vuông tại A , đường cao AH có:
AH.BC = A . B AC ⇒ AH.10 = 6.8 6.8 24 ⇒ AH = = = 4,8 (cm). 10 5 Vậy AH = 4,8 cm.
Câu 4. (2,0 điểm)
Cho tam giác ABC nhọn nội tiếp đường tròn (O) . Hai đường cao BM , CN cắt nhau tại H
(M ∈ AC , N ∈ AB) .
a) Chứng minh AMHN là tứ giác nội tiếp.
b) Chứng minh AN.BC = AC.MN và OA ⊥ MN . Lời giải
a) Do BM , CN là đường cao nên  =  ANH AMH = 90°.
Xét tứ giác AMHN có  + 
ANH AMH = 90° + 90° =180°.
Mà hai góc này ở vị trí đối diện nên tứ giác AMHN là tứ giác nội tiếp.
b) Ta có BM , CN là đường cao nên  =  ANH AMH = 90°.
⇒ B , M , N , C cùng thuộc đường tròn đường kính BC .
SẢN PHẨM CỦA NHÓM: WORD-GIẢI-TÁCH CHUYÊN ĐỀ VÀO 10 CÁC TỈNH  Trang 3 
TUYỂN TẬP ĐỀ TUYỂN SINH VÀO 10 – NĂM 2024-2025 ⇒  = 
AMN ABC (góc ngoài của đỉnh đối diện tứ giác nội tiếp).   =  AMN ABC ( cmt) Xét A ∆ MN và A ∆ BC có:   BAC chung ⇒ A ∆ MN A
∆ BC (g.g) ⇒ MN AN =
⇒ AN.BC = MN.AC . BC AC
Kẻ tiếp tuyến Ax của (O) tại A . Khi đó Ax ⊥ OA  = 
CAx ABC (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn AC ).  =  ABC AMN ( cmt) ⇒  = 
CAx AMN ⇒ Ax // MN .
Mà Ax ⊥ OA ⇒ MN ⊥ OA (đpcm).
Câu 5. (1,0 điểm) Cho phương trình 2 x − ( m + ) 2 2
1 x + m + 2 = 0 ( m là tham số). Tìm cả các giá trị nguyên của m để
phương trình đã cho có hai nghiệm phân biệt x và x sao cho biểu thức x x 1 2 = có giá trị nguyên. 1 2 P x + x 1 2 Lời giải
Ta có ∆ = ( m + )2 − ( 2 m + ) 2 2 2 1 4
2 = 4m + 4m +1− 4m −8 = 4m − 7
Để phương trình có hai nghiệm phân biệt x , x ⇔ ∆ > 0 ⇔ 4m − 7 > 0 7 ⇔ > 1 2 m 4
x + x = 2m +1
Áp dụng định lý Vi -ét 1 2  2 x x = m +  2 1 2 2 2 2 Khi đó : x x m + 2
4m + 8 4m −1+ 9 9 1 2 P = = ⇒ 4P = = = 2m −1+ x + x 2m +1 2m +1 2m +1 2m +1 1 2
4P nguyên khi và chỉ khi 9 nguyên hay 92m+1hay2m+1∈U(9)={ 1 ± ; 3 ± ;± } 9 2m +1 Ta có bảng sau 2m +1 9 − 3 − 1 − 1 3 9 m 5( − L) 2( − L) 1( − L) 0(L) 1(L) 4(TM ) 2 Với + m = 4 thì 4 2 P = = 2(tm) 2.4 +1
Vậy m = 4 thì phương trình đã cho có hai nghiệm phân biệt x , x sao cho biểu thức x x 1 2 P = có 1 2 x + x 1 2
giá trị nguyên. --------------------------------- Hết ---------------------------------
SẢN PHẨM CỦA NHÓM: WORD-GIẢI-TÁCH CHUYÊN ĐỀ VÀO 10 CÁC TỈNH  Trang 4 
Document Outline

  • Doc1
  • 9-DE THI VAO 10- SO CAO BANG-2024