Đề tuyển sinh lớp 10 THPT năm 2018 – 2019 sở GD và ĐT Hải Dương

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT HẢI DƯƠNG NĂM HỌC 2018-2019 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Ngày thi: Ngày 05 tháng 5 năm 2018
(Đề thi gồm: 01 trang) Câu 1 (2,0 điểm):
1) Giải phương trình: 3x 1  x 1  3x 1 2x  2  x 1 2 3
 x 17  y 3
 1 2y 17  y x  5
2) Giải hệ phương trình:      x  2y  1 
x 1 2y y  2 Câu 2 (2,0 điểm):
1) Cho hai hàm số bậc nhất y = x –3 và   2 y m   1 x  2m  3
Với giá trị nào của m thì đồ thị của các hàm số trên cắt nhau tại một điểm có hoành độ bằng -1  1 1  x 1 2) Rút gọn biểu thức:  A     : 1 với a  ; 0 a  1  x  x x 1 x  2 x 1 Câu 3 (2,0 điểm):
1) Một ô tô đi từ Hải Dương đến Hạ Long với quãng đường dài 100km.
Đến Hạ Long nghỉ lại 8h20 phút rồi quay lại Hải Dương hết tổng cộng 12h.
Biết vận tốc lúc về lớn hơn lúc đi 10km/h. Tính vận tốc lúc đi của ô tô. 2) Cho phương trình 2 2
x  2mx  m  2  0 Gọi hai nghiệm của phương trình là x x tìm m để 3 3 x  x 10 2 1, 2 1 2 Câu 4 (3,0 điểm):
Cho tam giác ABC nội tiếp đường tròn (O) đường kính BC. Kẻ AH  BC.
Gọi M và N là các hình chiếu vuông góc của H trên AB và AC 1) Chứng minh 2 AC  CH.CB.
2) Chứng minh tứ giác BMNC là tứ giác nội tiếp và AC.BM + AB.CN =AH. BC
3) Đường thẳng đi qua A cắt HM tại E và cắt tia đối của tia NH tại F. Chứng minh BE // CF Câu 5 (1,0 điểm):
Cho phương trình ax2  bx  c  0 a  0 có hai nghiệm x ;x thỏa mãn 1 2 2 3a  ab  ac
0  x  x  2 . Tìm giá trị nhỏ nhất của biểu thức L  1 2 2 2 5a  3ab  b
Họ và tên thí sinh: …………………………Số báo danh: …………………………
Chữ ký của giám thị 1: …………………….Chữ ký của giám thị 2: ………………
Đào Văn Thắng – THCS Tân Hương
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN VÀ BIỂU ĐIỂM CHẤM MÔN TOÁN HẢI DƯƠNG
KÌ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2018 - 2019
Ngày thi: 04 tháng 5 năm 2018 I) HƯỚNG DẪN CHUNG
- Thí sinh làm bài theo cách khác nhưng đúng vẫn cho điểm tối đa.
- Sau khi cộng điểm toàn bài, điểm lẻ đến 0,25 điểm.
II) ĐÁP ÁN VÀ BIỂU ĐIỂM CHẤM Câu Ý Nội dung Điểm 1 1 1,00
3x 1  x 1 3x 12x  2  x 1 0,25 2 0,25 0,25 0,25 2 1,00 3
 x 17  y 3
 1 2y 17  y x  5 0,25      x  2y  1 0,25 
x 1 2y y  2 0,25 KL 0,25 2 1 1,00
-Đk để 2 đt cắt nhau là 2 m  1  1  m  0 0,25 -Thay x =- 1 vào y = x-3 =-4 0,25
-Thay x =-1 và y = -4 vào hàm số   2 y m   1 x  2m  3 được 0,25 m =0 (Loại); m = 2 (TM) 0,25 ĐS: m =2 2 1,00  1 1  x 1 A     : 1 0,25  x  x x 1 x  2 x 1    1 1  x 1 = : 1 0,25  x  x    1 x 1  2 x         1  2 x   1 1 x   .1  x  1 x x 0,25  1  x  1 0,25  x 1 x 1  1   x x x 3 1 1,00
Gọi vận tốc lúc đi của ô tô là x km/h (x>0)
Vận tốc lúc về là x +10 km/h 0,25 Thời gian lúc đi là 100 h x
Đào Văn Thắng – THCS Tân Hương Thời gian lúc đi là 100 0,25 h x  10 Theo đề bài ta có PT 0,25 100 100 25    12 x x  10 3 0,25 ĐS x =50 km/h 2 Cho phương trình 2 2
x  2mx  m  2  0 Gọi hai nghiệm của 1,00
phương trình là x x tìm m để 3 3 x  x 10 2 1, 2 1 2
'  2  0 pt có hai nghiệm phân biệt với mọi m. x  x  2m 0,25 1 2 2 x .x  m  2 1 2
Bình phương hai vế và biến đổi được: 0,25 
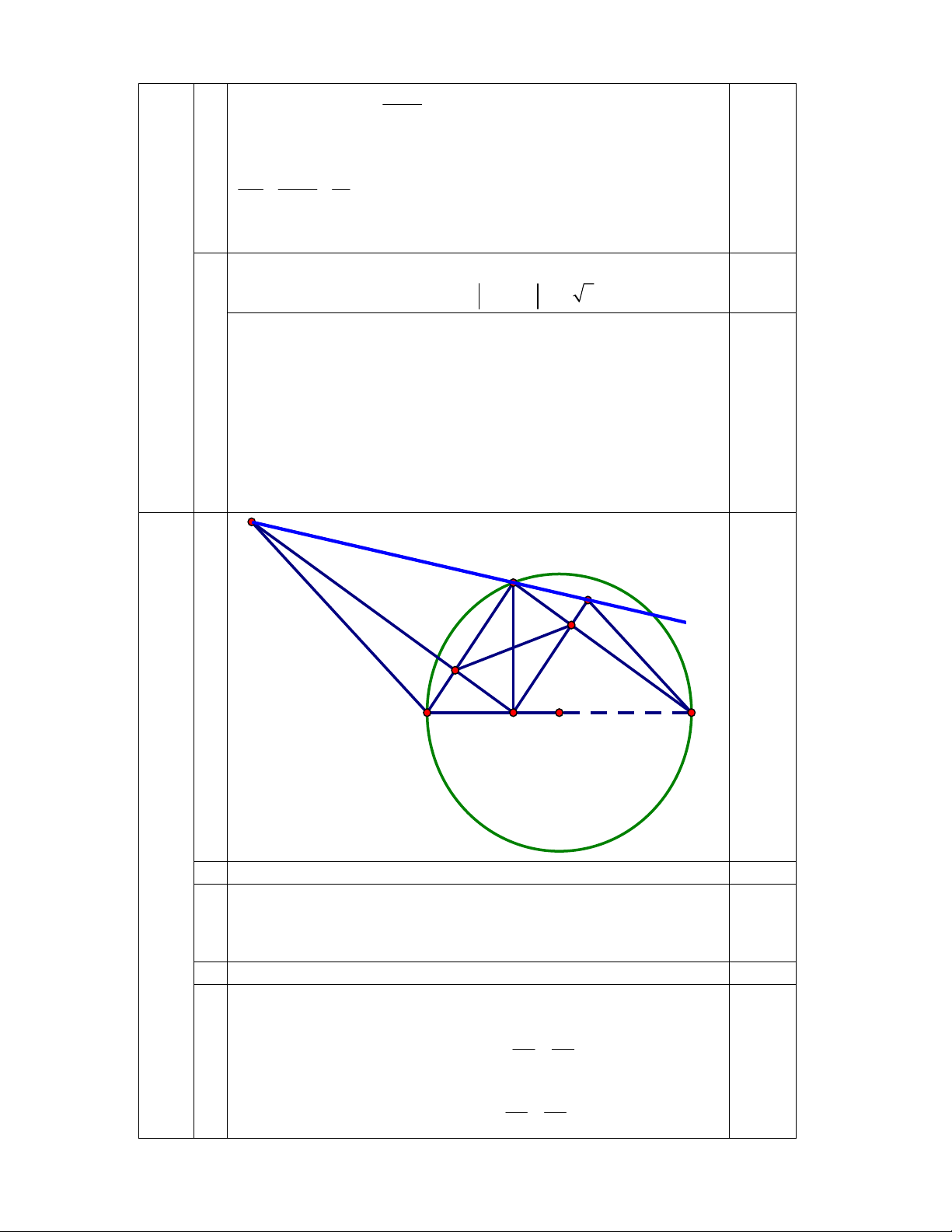
x  x 2  4x .x  x  x 2  x .x   200 1 2 1 2 1 2 1 2     0,25 Thay VI-ét ta có 2  3m  2  5   m  1 2 3m  2  5 0,25 4 E A 0,25 F x M N C B H O 1 0,75 - Chỉ ra góc BAC vuông 0,25 -Áp dụng hệ thức 2
b  b'.a vào tam giác vuông ABC ta có 0.25 2 AC  CH.CB. 0,25 2 1,00
-Chỉ ra góc MNA bằng góc NAH bằng góc ABH
- Suy ra tứ giác BMNC là tứ giác nội tiếp 0,25
- Chỉ ra  BMH   AHC suy ra BM BH  suy ra BM.AC = AH AC 0.25 AH. BH
Chỉ ra  CNH   AHB suy ra CN CH  suy ra CN.AB = 0,25 AH AB
Đào Văn Thắng – THCS Tân Hương AH. CH 0,25
-Cộng theo vế suy ra điều phải chứng minh 3 1,00
- Có HE //AC nên góc AEM bằng góc NAF suy ra ANF  EMA(g.g) AN NF    AN.AM NF.ME ME AM 0,25
- Chỉ ra HNC  BMH(g.g) BM MH    BM.NC  MH.NH HN NC  AN.AM NF.ME 0,25 - Có AM.AN = MH.NH Kết luận NF.ME =BM.NC ME BM   và     0 BME FNC( 90 ) NC NF
- Suy ra BME FNC(c.g.c) 0,25    BEM  FCN Mà  
AEM  FAC ( góc đồng vị HE // AC ) Ta có    AEB  AEM  BEM Và   
xFC  FCN  FAC ( góc ngoài tam giác AFC ) 0,25 Nên   AEB  xFC
Suy ra BE // CF (có góc ở vị trí đồng vị   AEB  xFC ) 5 1,00 b c 2 3   3a  ab  ac 3  x  x  x .x a a 1 2 1 2 L    2 2 2 5a  3ab  b b  b 
5  3x  3x  x  x 2 1 2 1 2 5  3  a  a    0,25
Biến đổi và đánh giá 0  x  x  2 ta có 1 2 1 x  2 . x  2  x .x 1   2  1 2  0,25 3   3 L x .x  x  x  3 1 2 1 2 1  0,25 L  3 Min L = 1/3 0,25
Đào Văn Thắng – THCS Tân Hương