Đề tuyển sinh lớp 10 THPT năm 2019 – 2020 môn Toán sở GD&ĐT Bạc Liêu

SỞ GIÁO DỤC KHOA HỌC VÀ CÔNG NGHỆ
KỲ THI TUYỂN SINH LỚP 10 THPT BẠC LIÊU NĂM HỌC 2019 – 2020 --------------
Môn thi: TOÁN (Không chuyên) ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian phát đề) Ngày thi: 07/6/2019 ------------------- ðỀ BÀI
Câu 1: (4,0 ñiểm) Rút gọn biểu thức: a) A = 45 − 2 20 − b) B = − ( − )2 3 5 27 3 12 . 3 − 5 Câu 2: (4,0 ñiểm) 2x − y = 4
a) Giải hệ phương trình x + y = 5  b) Cho hàm số 2
y = 3x có ñồ thị ( P) và ñường thẳng (d ) : y = 2x +1. Tìm tọa ñộ gia0 ñiểm của
(P) và (d ) bằng phép tính. Câu 3: (6,0 ñiểm) Cho phương trình: 2
x − 2mx − 4m − 5 ( ) 1 (m là tham số). a) Giải phương trình ( ) 1 khi m = 2 − .
b) Chứng minh phương trình ( )
1 luôn có nghiệm với mọi giá trị của m.
c) Gọi x ; x là hai nghiệm của phương trình ( ) 1 . Tìm m ñể: 1 2 1 33 2
x − m −1 x + x − 2m + = 762019 . 1 ( ) 1 2 2 2 Câu 4: (6,0 ñiểm)
Trên nửa ñường tròn ñường kính AB, lấy hai ñiểm I, Q sao cho I thuộc cung AQ. Gọi C là giao
ñiểm hai tia AI và BQ; H là giao ñiểm hai dây AQ và BI.
a) Chứng minh tứ giác CIHQ nội tiếp.
b) Chứng minh: CI.AI = HI.BI .
c) Biết AB = 2R . Tính giá trị biểu thức: M = AI.AC + B . Q BC theo R.
-----------Hết----------- HƯỚNG DẪN GIẢI.
Câu 1: (4,0 ñiểm) Rút gọn biểu thức: a) A = 45 − 2 20 − b) B = − ( − )2 3 5 27 3 12 3 − 5 Giải: a) 2 2 A = 45 − 2 20 =
3 .5 − 2 2 .5 = 3 5 − 2.2 5 = − 5 − − b) B = − ( − )2 3 5 27 3 5 3 3 3 12 = − 3 − 12 3 − 5 3 − 5 3( 5 − 3) = − (−3+ 12) (do 2 3 < 12 ⇒ 3 < 12 ) 3 − 5 = −3 + 3 − 12 = − 12 = 2 − 3 . Câu 2: (4,0 ñiểm) 2x − y = 4
a) Giải hệ phương trình x + y = 5  b) Cho hàm số 2
y = 3x có ñồ thị ( P) và ñường thẳng (d ) : y = 2x +1. Tìm tọa ñộ giao ñiểm của
(P) và (d ) bằng phép tính. Giải: 2x − y = 4 3  x = 9 x = 3 a)  ⇔  ⇔  x + y = 5 y = 5 − x y = 2   
Vậy hệ phương trình có nghiệm là: ( x; y ) = (3; 2)
b) Phương trình hoành ñộ giao ñiểm: 2 2
3x = 2x +1 ⇔ 3x − 2x −1 = 0 (*)
Phương trình (*) có hệ số: a = 3; b = 2 − ; c = 1
− ⇒ a + b + c = 0 − ⇒ c 1
Phương trình (*) có hai nghiệm: x = 1; x = = 1 2 a 3 - Với 2
x = 1 ⇒ y = 3.1 = 3 ⇒ A 1;3 1 ( ) 2 −1  −1 1  −1 1  - Với x = ⇒ y = 3. = ⇒ B ; 2     3  3  3  3 3   1 − 1 
Vậy tọa ñộ giao ñiểm của ( P) và (d ) là A(1;3) và B ;   .  3 3  Câu 3: (6,0 ñiểm) Cho phương trình: 2
x − 2mx − 4m − 5 ( ) 1 (m là tham số). a) Giải phương trình ( ) 1 khi m = 2 − .
b) Chứng minh phương trình ( )
1 luôn có nghiệm với mọi giá trị của m.
c) Gọi x ; x là hai nghiệm của phương trình ( ) 1 . Tìm m ñể: 1 2 1 33 2
x − m −1 x + x − 2m + = 762019 1 ( ) 1 2 2 2 Giải: a) Thay m = 2 − vào phương trình ( ) 1 ta có: x = −3 2
x + 4x + 3 = 0 ⇔ x ( x + 3) + ( x + 3) = 0 ⇔ ( x + 3)( x + ) 1 = 0 ⇔ x = −1  Vậy với m = 2
− thì phương trình có tập nghiệm S = {−3; − } 1
b) Ta có: ∆ = m − (− m − ) = (m + )2 ' 2 4 5 2 +1 > 0, m ∀ Do ñó phương trình ( )
1 luôn có hai nghiệm với mọi giá trị của m. c) Do phương trình ( )
1 luôn có hai nghiệm với mọi giá trị của m, gọi x ; x là hai nghiệm của 1 2 phương trình ( ) 1
x + x = 2m
Áp dụng ñịnh lí Vi-ét ta có: 1 2 x x = 4 − m − 5  1 2 1 33 Ta có: 2
x − m −1 x + x − 2m + = 762019 1 ( ) 1 2 2 2 2
⇔ x − 2(m − )
1 x + 2x − 4m + 33 = 1524038 1 1 2 2
⇔ x − 2mx − 4m − 5 + 2 x + x = 1524000 1 ( 1 2 ) 1
⇔ 2( x + x = 1524000 (do x là nghiệm của ( ) 1 nên 2
x − 2mx − 4m − 5 = 0 ) 1 2 ) 1 1 1
⇔ 2.2m =1524000 ⇔ m = 381000
Vậy m = 381000 thỏa mãn yêu cầu bài toán. Câu 4: (6,0 ñiểm)
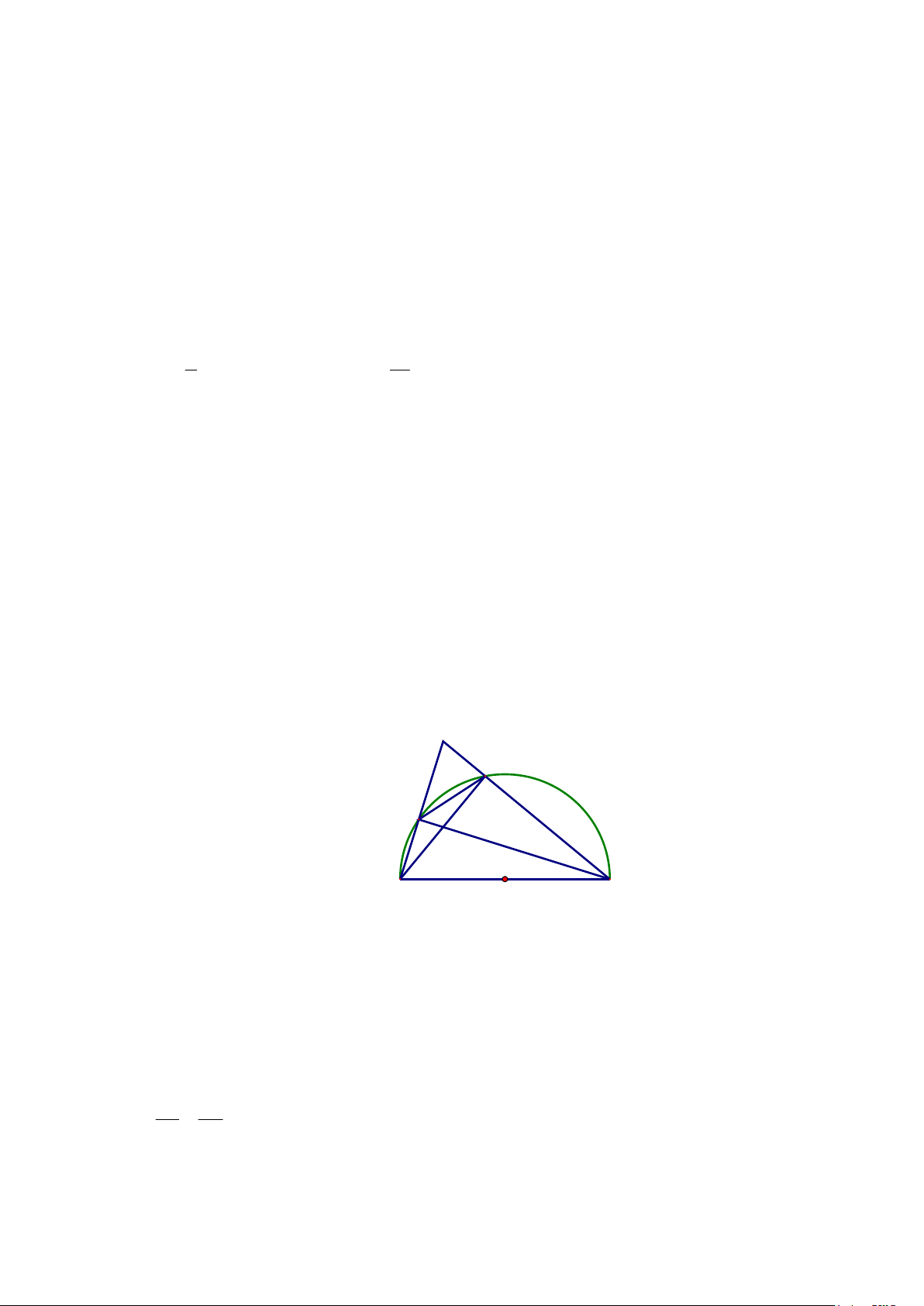
Trên nửa ñường tròn ñường kính AB, lấy hai ñiểm I, Q sao cho I thuộc cung AQ. Gọi C là giao
ñiểm hai tia AI và BQ; H là giao ñiểm hai dây AQ và BI.
a) Chứng minh tứ giác CIHQ nội tiếp.
b) Chứng minh: CI.AI = HI.BI .
c) Biết AB = 2R . Tính giá trị biểu thức: M = AI.AC + B . Q BC theo R. Giải: C Q I H A O B a) Ta có: = 0 AIB
AQB = 90 (góc nội tiếp chắn nửa ñường tròn) ⇒ = 0 CIH CQH = 90 Xét tứ giác CIHQ có + 0 0 0 CIH CQH = 90 + 90 = 180
⇒ tứ giác CIHQ nội tiếp
b) Xét ∆AHI và B ∆ CI có: = 0 AIH BIC = 90    ⇒ A ∆ HI ∽ B
∆ CI ( g.g) = IAH IBC  AI HI ⇒ =
⇒ CI.AI = HI.BI BI CI
c) Ta có: M = AI.AC + BQ.BC = AC ( AC − IC ) + BQ ( BQ + QC ) 2 2
= AC − AC.IC + BQ + B . Q QC 2 2 2
= AQ + QC − AC.IC + BQ + B . Q QC = ( 2 2
AQ + BQ ) + QC (QC + BQ) − AC.IC 2
= AB + QC.BC − AC.IC
Tứ giác AIBQ nội tiếp (O) ⇒ = CIQ
CBA (cùng phụ với AIQ ) Xét C ∆ IQ và C ∆ BA có: ACB chung    ⇒ C ∆ IQ∽ CB ∆ A ( g.g ) = CIQ CBA  IC QC ⇒ =
⇒ QC.BC = AC.IC BC AC
⇒ QC.BC − AC.IC = 0
Suy ra: M = AB = ( R)2 2 2 2 = 4R
----------- HẾT -----------