Đề tuyển sinh lớp 10 THPT năm 2019 – 2020 môn Toán sở GD&ĐT Bình Định

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO 10 THPT BÌNH ĐỊNH NĂM HỌC 2019 - 2020 ----------------- MÔN THI: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 06/06/2019
Thời gian làm bài: 120 phút (không kể thời gian phát ñề) -------------------------- ðỀ BÀI
1. Giải phương trình: 3(x −1) = 5x + 2 .
2. Cho biểu thức: A = x + 2 x −1 +
x − 2 x −1 với x ≥ 1
a) Tính giá trị biểu thức A khi x = 5 .
b) Rút gọn biểu thức A khi 1 ≤ x ≤ 2 . 1. Cho phương trình: 2
x − (m −1)x − m = 0 . Tìm m ñể phương trình trên có một nghiệm
bằng 2 . Tính nghiệm còn lại.
2. Trong mặt phẳng tọa ñộ Oxy cho ba ñường thẳng
d : y = 2x −1; d : y = ;
x d : y = 3 − x + 2. 1 2 3
Tìm hàm số có ñồ thị là ñường thẳng d song song với ñường thẳng d ñồng thời ñi qua giao ñiểm của hai 3
ñường thẳng d và d . 1 2 2
Hai ñội công nhân cùng làm chung trong 4 giờ thì hoàn thành ñược
công việc. Nếu làm riêng thì thời gian 3
hoàn thành công việc ñội thứ hai ít hơn ñội thứ nhất là 5 giờ. Hỏi nếu làm riêng thì thời gian hoàn thành công
việc của mỗi ñội là bao nhiêu?
Cho ñường tròn tâm O , bán kính R và một ñường thẳng d không cắt ñường tròn (O) . Dựng ñường thẳng
OH vuông góc với ñường thẳng d tại ñiểm H . Trên ñường thẳng d lấy ñiểm K (khác ñiểm H ), qua K
vẽ hai tiếp tuyến KA và KB với ñường tròn (O) , ( A và B là các tiếp ñiểm) sao cho A và H nằm về hai
phía của ñường thẳng OK .
a) Chứng minh tứ giác KAOH nội tiếp ñược trong ñường tròn.
b) ðường thẳng AB cắt ñường thẳng OH tại ñiểm I . Chứng minh rằng IA⋅ IB = IH ⋅ IO và I là ñiểm cố
ñịnh khi ñiểm K chạy trên ñường thẳng d cố ñịnh.
c) Khi OK = 2R, OH = R 3 . Tính diện tích tam giác KAI theo R . x > y 2 2 x + y
Cho x, y là hai số thực thỏa 
. Tìm giá trị nhỏ nhất của biểu thức P = . xy =  1 x − y
LỜI GIẢI ðỀ TUYỂN SINH VÀO 10 BÌNH ðỊNH NĂM HỌC 2019-2020 Câu 1.
1. Giải phương trình: 3(x −1) = 5x + 2 .
2. Cho biểu thức: A = x + 2 x −1 +
x − 2 x −1 với x ≥ 1
a) Tính giá trị biểu thức A khi x = 5 .
b) Rút gọn biểu thức A khi 1 ≤ x ≤ 2 . Lời giải 1. Ta có 5
3(x −1) = 5x + 2 ⇔ 3x − 3 = 5x + 2 ⇔ 2x = 5 − ⇔ x = − . 2 5
Vậy phương trình ñã cho có nghiệm là x = − . 2 2.
a) Khi x = 5 , ta có
A = 5 + 2 5 −1 + 5 − 2 5 −1
= 5 + 2 4 + 5 − 2 4 = 5 + 2⋅ 2 + 5 − 2⋅ 2 = 9 + 1 = 3 +1 = 4 .
Vậy khi x = 5 thì A = 4 .
b) Với 1 ≤ x ≤ 2 , ta có A = x + 2 x −1 + x − 2 x −1
= x −1+ 2 x −1 +1 + x −1− 2 x −1 +1 2 2
= ( x −1 +1) + ( x −1 −1) | = x −1 +1| + | x −1 −1|
= x −1 +1+1− x −1 (1 ≤ x ≤ 2 ⇒ 0 ≤ x −1 ≤ 1 ⇒ x −1 −1 ≤ 0) = 2.
Vậy khi 1 ≤ x ≤ 2 thì A = 2 . Câu 2. 1. Cho phương trình: 2
x − (m −1)x − m = 0 . Tìm m ñể phương trình trên có một nghiệm bằng 2 . Tính nghiệm còn lại.
2. Trong mặt phẳng tọa ñộ Oxy cho ba ñường thẳng
d : y = 2x −1; d : y = ;
x d : y = −3x + 2. 1 2 3
Tìm hàm số có ñồ thị là ñường thẳng d song song với ñường thẳng d ñồng thời ñi qua giao ñiểm của hai 3
ñường thẳng d và d . 1 2 Lời giải 1. 2
x − (m −1)x − m = 0. (1)
Thay x = 2 vào phương trình (1) ta ñược
22 − (m −1) ⋅ 2 − m = 0 ⇔ 4 − 2m + 2 − m = 0 ⇔ 3m = 6 ⇔ m = 2.
Thay m = 2 vào phương trình (1) ta ñược 2
x − x − 2 = 0.
Ta có các hệ số: a − b + c = 0 nên phương trình có hai nghiệm phân biệt là x = 1 − ; x = 2 . 1 2
Vậy với m = 2 phương trình ñã cho có một nghiệm bằng 2 , nghiệm còn lại là −1. 2.
Phương trình ñường thẳng d : ax + b (a, b ∈ ℝ) . a = −3 d d ⇒ 
⇒ d : y = −3x + , b (b ≠ 2). 3 b ≠  2
Tọa ñộ giao ñiểm của hai ñường thẳng d , d là nghiệm của hệ phương trình 1 2
 y = 2x −1 x = 2x −1 x = 1  ⇔  ⇔  ⇒ ( A 1;1)  y = x   y = x y =  1 (
A 1;1) ∈ d : y = −3x + b ⇒ 1 = −3⋅1+ b ⇔ b = 4 (TM).
Vậy phương trình ñường thẳng cần tìm là d : y = 3 − x + 4 . 2 Câu 3.
Hai ñội công nhân cùng làm chung trong 4 giờ thì hoàn thành ñược công việc. Nếu làm 3
riêng thì thời gian hoàn thành công việc ñội thứ hai ít hơn ñội thứ nhất là 5 giờ. Hỏi nếu làm riêng thì
thời gian hoàn thành công việc của mỗi ñội là bao nhiêu? Lời giải
Gọi thời gian ñội thứ nhất làm riêng hoàn thành công việc là x (giờ, x > 5 ).
Thời gian ñội thứ hai làm riêng hoàn thành công việc là y (giờ, y > 0 ). 1 1
Mỗi giờ ñội thứ nhất làm ñược
công việc, ñội thứ hai làm ñược công việc. x y 4 4
Trong 4 giờ ñội thứ nhất làm ñược
công việc, ñội thứ hai làm ñược công việc. x y
Theo ñề ta có hệ phương trình  4 4 2 + =  (1)  x y 3 x − y =  5 (2)
(2) ⇔ x = y + 5 thế vào (1) ta ñược 4 4 2 + =
⇒ 6y + 6( y + 5) = y( y + 5) y + 5 y 3  y = −3 (ktm) 2
⇔ y − 7 y − 30 = 0 ⇔  y =10⇒ x =  15
Vậy nếu làm riêng thì thời gian hoàn thành công việc của ñội thứ nhất là 15 giờ, ñội thứ hai là 10 giờ. Câu 4.
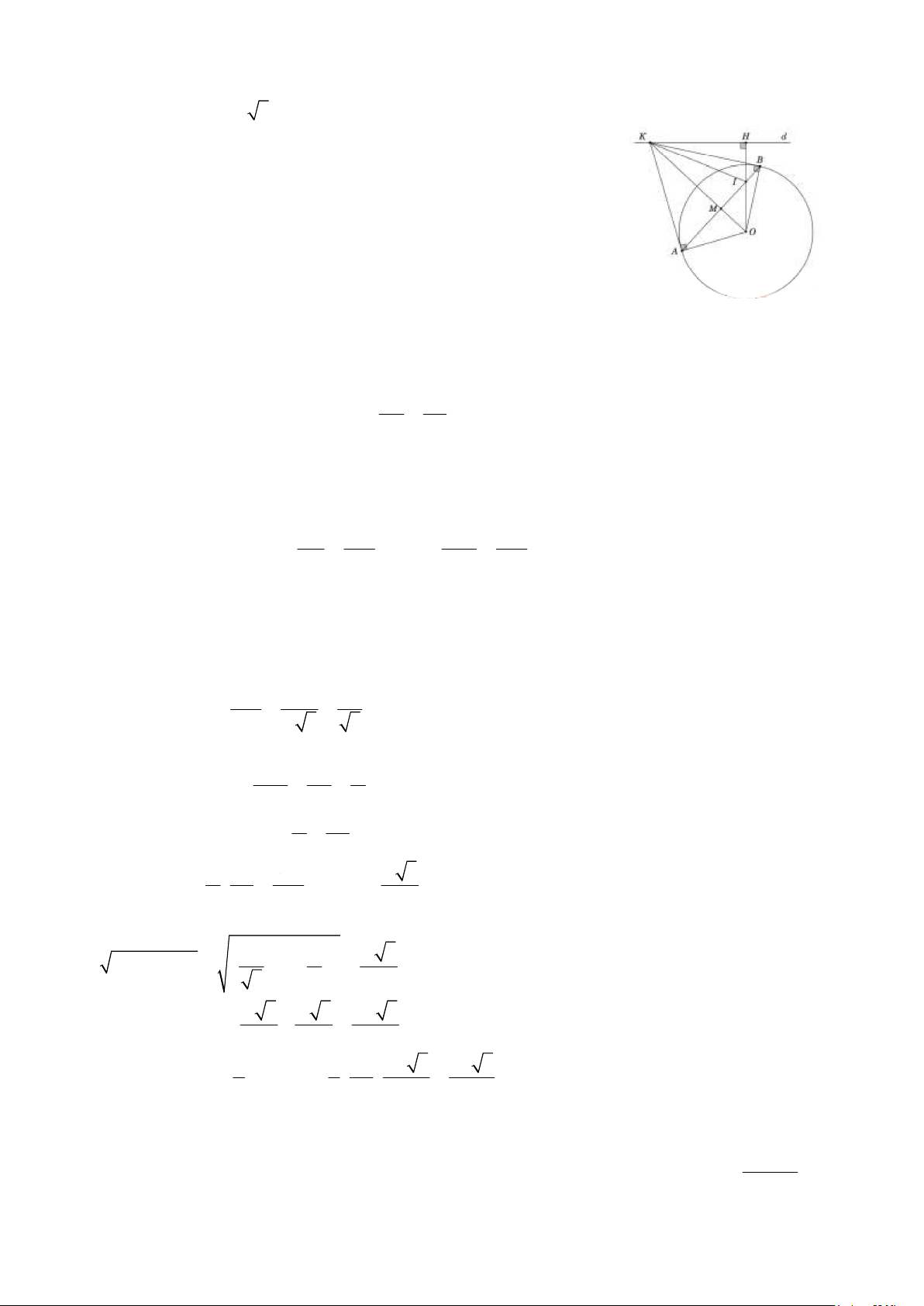
Cho ñường tròn tâm O , bán kính R và một ñường thẳng d không cắt ñường tròn (O) . Dựng
ñường thẳng OH vuông góc với ñường thẳng d tại ñiểm H . Trên ñường thẳng d lấy ñiểm K (khác
ñiểm H ), qua K vẽ hai tiếp tuyến KA và KB với ñường tròn (O) , ( A và B là các tiếp ñiểm) sao
cho A và H nằm về hai phía của ñường thẳng OK .
a) Chứng minh tứ giác KAOH nội tiếp ñược trong ñường tròn.
b) ðường thẳng AB cắt ñường thẳng OH tại ñiểm I . Chứng minh rằng IA⋅ IB = IH ⋅ IO và I là ñiểm cố
ñịnh khi ñiểm K chạy trên ñường thẳng d cố ñịnh.
c) Khi OK = 2R, OH = R 3 . Tính diện tích tam giác KAI theo R . Lời giải ° a) Ta có
KAO = 90 (KA ⊥ AO) , °
KHO = 90 (OH ⊥ KH ) °
Xét tứ giác KAOH có KAO + KBO = 180
nên là tứ giác nội tiếp. ° b) Ta có
KBO + KAO = 180 nên KAOB là tứ giác nội tiếp và ñỉnh H , B, A cùng nhìn cạnh OK dưới một
góc vuông nên năm ñiểm K , ,
A B, O, H cùng thuộc ñường tròn ñường kính OK
Xét tam giác IAH và tam giác IOB có
HIA = BIO (ñối ñỉnh) và
AHI = ABO (hai góc nội tiếp cùng chắn IA IO
cung AO ). Do ñó ∆IAH ∽ ∆IOB (g.g) ⇒ =
⇒ IA⋅ IB = IH ⋅ IO . IH IB
Xét tứ giác AOBH có
OHB là góc nội tiếp chắn cung OB,
OBA là góc nội tiếp chắn cung OA; Mà
OA = OB = R nên OHB = OBA . Xét O ∆ IB và O ∆ BH có BOH góc chung và
OHB = OBA (cmt). 2 2 OI OB OB R Do ñó O ∆ IB ∽ O
∆ BH (g.g) ⇒ = ⇒ OI = = . OB OH OH OH
Ta lại có ñường thẳng d cố ñịnh nên OH không ñổi ( OH ⊥ d ).
Vậy ñiểm I cố ñịnh khi K chạy trên ñường thẳng d cố ñịnh.
c) Gọi M là giao ñiểm của OK và AB
Theo tính chất tiếp tuyến ta có KA=KB;
Lại có OA = OB = R nên OK là ñường trung trực của AB, suy ra AB ⊥ OK tại M và MA = MB . 2 2 R R R
Theo câu b) ta có OI = = = . OH R 3 3 Xét O
∆ AK vuông tại A , có 2 2 OA R R 2
OA = OM ⋅OK ⇔ OM = = = OK 2R 2 R 3R
Suy ra KM = OK − OM = 2R − = 2 2 2 R 3R 3R R 3 2
AM = OM ⋅ KM = ⋅ = ⇒ AM = 2 2 4 2 Xét O
∆ MI vuông tại M , có 2 2  R   R  R 3 2 2
MI = OI − OM = − =      3   2  6 R 3 R 3 2R 3
Suy ra AI = AM + MI = + = 2 6 3 2 1 1 3R 2R 3 R 3
Diện tích ∆AKI là S = AI ⋅ KM = ⋅ ⋅ = . 2 2 2 3 2 x > y 2 2 x + y Câu 5.
Cho x, y là hai số thực thỏa 
. Tìm giá trị nhỏ nhất của biểu thức P = . xy =  1 x − y Lời giải
Với x > y, xy = 1, ta có 2 2 2 x + y
(x − y) + 2xy 2 P = = = x − y + x − y x − y x − y 2
Vì x > y ⇒ x − y > 0; > 0 và xy = 1. x − y 2
Áp dụng bất ñẳng thức Cô-si cho hai số dương x − y; , ta có x − y 2 2(x − y) x − y + ≥ 2 = 2 2 = 2 2 x − y x − y Suy ra min P = 2 2 . 2 Dấu ñẳng thức xảy ra 2 ⇔ x − y =
⇔ (x − y) = 2 ⇔ x − y = 2 ⇔ x = y + 2 . x − y  6 − 2  y = 2 Mà 2 2
xy = 1 ⇒ ( y + 2) y = 1 ⇔ y + 2 y = 1 ⇔ y + 2 y −1 = 0 ⇔  − 6 − 2  y =  2  2 + 6  2 − 6 x = x =  2  2
Vậy min P = 2 2 tại  hoặc   − 2 + 6  − 2 − 6 y =  y = .   2  2