Đề tuyển sinh lớp 10 THPT năm 2019 – 2020 môn Toán sở GD&ĐT Điện Biên
Giới thiệu nội dung đề thi và lời giải chi tiết đề thi tuyển sinh vào lớp 10 hệ THPT năm học 2019 – 2020 môn Toán sở GD&ĐT Điện Biên, kỳ thi được diễn ra vào ngày …/06/2019. Mời các bạn đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024 872 tài liệu
Môn: Môn Toán 1.3 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT ĐIỆN BIÊN NĂM HỌC 2019 - 2020 --------------- MÔN THI: TOÁN ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề) ----------------------- ĐỀ BÀI Câu 1. (2,5 ñiểm) x + 5 x −1 7 x − 3 Cho biểu thức: A = và B = + x − 3 x + 3 x − 9 1. Tính A khi x = 25. 2. Rút gọn biểu thức B. A
3. Tìm giá trị nhỏ nhất của . B Câu 2. (2,5 ñiểm) 1. Giải phương trình: a) 2 x − 5x + 4 = 0 b) 4 2 x + x − 6 = 0 2x − y = 7
2. Giải hệ phương trình: x − 2y =−1 Câu 3. (1,0 ñiểm) Cho phương trình: 2
x + ax + b +1= 0 (a, b là các tham số). Tìm a, b ñể phương trình có 2 nghiệm x1, x2 thỏa x − x = 3 1 2 mãn: 3 3 x − x = 9 1 2 Câu 4. (3,0 ñiểm)
Cho tứ giác ABCD nội tiếp (O; R) và có hai ñường chéo AC, BD vuông góc với nhau tại I (I khác O). Kẻ ñường kính CE.
1. Chứng minh tứ giác ABDE là hình thang cân. 2. Chứng minh: 2 2 2 2
AB + CD + BC + AD = 2 2 . R
3. Từ A, B kẻ các ñường thẳng vuông góc với CD lần lượt cắt BD, AC tại F và K. Tứ giác ABKF là hình gì? Câu 5. (1,0 ñiểm)
1. Tìm nghiệm nguyên của phương trình: 3 3 2
y = x + x + x +1.
2. Cho các số nguyên a, b, c thỏa mãn ab + bc + ca = 1. Chứng minh rằng: A = ( 2 + a )( 2 + b )( 2 1 1 1+ c ) là một số chính phương.
---------- HẾT ---------- Câu 1. (2,5 ñiểm) x + 5 x −1 7 x − 3 Cho biểu thức: A = và B = + x − 3 x + 3 x − 9 1. Tính A khi x = 25. 2. Rút gọn biểu thức B. A
3. Tìm giá trị nhỏ nhất của . B Hướng dẫn:
ðKXð: x ≥ 0, x ≠ 9 25 + 5 30 = = =
1. Với x = 25 (TMðK) => A 15 25 − 3 5 − 3 x −1 7 x − 3
( x −1)( x − 3) 7 x − 3 B = + = + x + 3 x − 9
( x + 3)( x − 3) x − 9 2. Có:
x − 4 x + 3 + 7 x − 3 x + 3 x x = = = x − 9 x − 9 x − 3 A x + 5 x x + 5 = : = B x − 3 x − 3 x 3. Có: ðK: x > 0. A x + 5 5 5 = = x + ≥ 2. x i = 2 5 B x x x => 5 x = ⇔ x =5(TM ) x Dấu "=" xảy ra <=>
MinA = 2 5 ⇔ x = 5 Vậy Câu 2. (2,5 ñiểm) 1. Giải phương trình: 2 x − 5x + 4 = 0 4 2 x + x − 6 = 0 a) b) 2x − y = 7 x −2y =−1
2. Giải hệ phương trình: Hướng dẫn: x = 1 2
(x − 2) = 0⇔ x = ± 2 2 − + = ⇔ 4 2 2 2 + − = ⇔ − + = ⇔ 1. a) x 5x 4 0 x x 6 0 (x 2)(x 3) 0 x = 4 b) 2
(x + 3) = 0(Voly) 2x − y = 7
4x − 2y = 14 3 x = 15 x = 5 ⇔ ⇔ ⇔ 2. x − 2 y = −1 x − 2 y = −1 x − 2 y = −1 y = 3 Câu 3. (1,0 ñiểm) Cho phương trình: 2
x + ax + b +1= 0 (a, b là các tham số). Tìm a, b ñể phương trình có 2 nghiệm x1, x2 thỏa x − x = 3 1 2 mãn: 3 3 x − x = 9 1 2 Hướng dẫn: 2 2 ∆ = − + = − − Ta có: a 4(b 1) a 4b 4 2
∆ ≥ 0 ⇔ a − 4b − 4≥ 0
ðể phương trình có nghiệm thì:
x − x = −a 1 2
x .x =b +1 Theo Vi-Et ta có: 1 2 x − x = 3 x − x = 3 1 2 1 2 2 ⇔
⇔ (x + x ) − x x = 3 1 2 1 2 3 3 2 2 x − x = 9
(x − x )(x + x x + x ) = 9 Mà: 1 2 1 2 1 1 2 2 2 2
⇔ ( − a) − b −1 = 3⇔ b = a − 4 2 b = a − 4 2 2 2 2
∆ = a − 4b − 4 = a − 4(a − 4) − 4 = 3 − a +12 Thay
vào biểu thức Delta ta có: 2
∆ ≥ 0 ⇔ −3a −12 ≥ 0 ⇔ − 2 ≤ a ≤ 2 ðK: 2 2 −a + ∆ −a + −3a +12 −a − ∆ −a − 3 − a +12 x = = ; x = = 1 2 2 2 2 2 => 2 2 −a + 3 − a +12 −a − 3 − a +12
x − x = 3 => x − x = − = 3 1 2 1 2 2 2 a =1 Do: 2
=> − 3a +12 = 9 =>
(TM ) => b = 3 − a=−1 a = 1 ± b = 3 − Vậy
thì pt có nghiệm thỏa mãn ñề bài. Câu 4. (3,0 ñiểm)
Cho tứ giác ABCD nội tiếp (O; R) và có hai ñường chéo AC, BD vuông góc với nhau tại I (I khác O). Kẻ ñường kính CE.
1. Chứng minh tứ giác ABDE là hình thang cân. 2 2 2 2
AB + CD + BC + AD = 2 2 . R 2. Chứng minh:
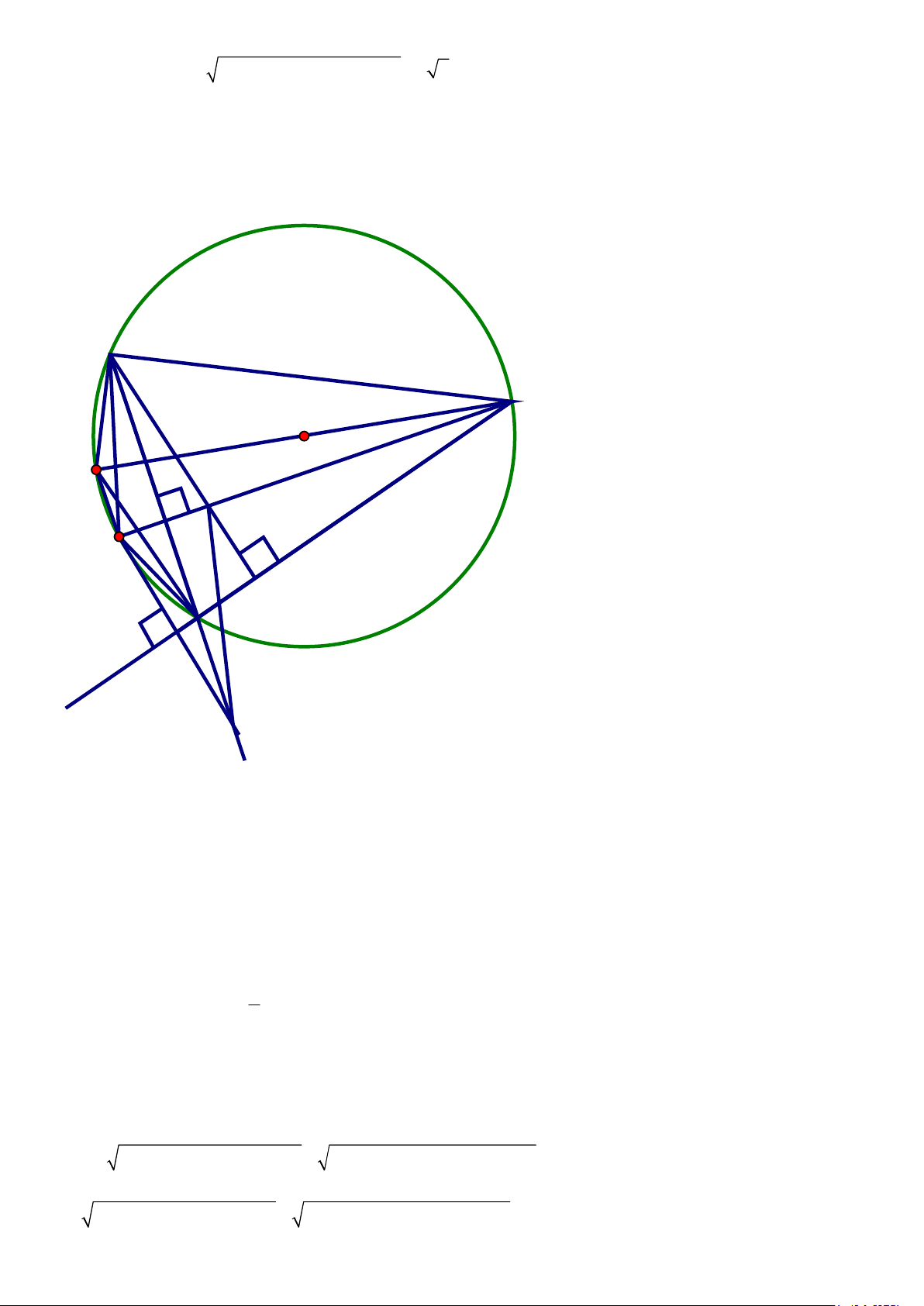
3. Từ A, B kẻ các ñường thẳng vuông góc với CD lần lượt cắt BD, AC tại F và K. Tứ giác ABKF là hình gì? Hướng dẫn: B C O E K I A D N M F 1. Có: 0
EAC = EBC = EDC = 90 (Góc nt chắn nửa ñường tròn)
⇒ EA ⊥ AC ⇒ ⊥ ⇒ EA BD ( AC)
EADB là hình thang (1) 0 BEC = BCE =90 Mà: 0 (cmt) IDC = ICD = 90 1 = = = Do: IDC BDC ADC BC BC 2 (Góc nt chắn ) = = ⇒ = ⇒ = => ICD
ACD BCE => EB AD EB AD (2)
Từ (1) và (2) => AEBD là hình thang cân. (ñpcm) 2 2 2 2 2 2 2 2 + + + = + + + 2. Có: AB CD BC AD (ED CD ) (BC
EB ) (Vì: AB = ED, AD = EB (cmt))
=> AB2 + CD2 + BC 2 + AD2 = (ED2 + CD2 ) + (BC2 + EB2 ) 2 2 2 2 (ñpcm)
= EC + EC = 2EC = 2.(2R) = 2 2R
3. Giả sử : AF ⊥ CD = M ; BK ⊥ CD = N = => MCA
IFA (Cùng phụ với CAM )
⇒ ∆ AFB cân tại A. => AB = AF (3)
⇒ IAB = IAF (ðường cao trong tam giác cân) ⊥ Mà: BK // AF (cùng DC )
⇒ IKB = IAF (SLT ) ⇒ = = IKB IAB ( IAF)
⇒ ∆ ABK cân tại B => BA = BK (4)
Từ (3) và (4) => AB = BK = AF.
=> AF//=BK => ABKF là HBH
Mặt khác: => ABKF là hình thoi. Câu 5. (1,0 ñiểm)
1. Tìm nghiệm nguyên của phương trình: 3 3 2
y = x + x + x +1.
2. Cho các số nguyên a, b, c thỏa mãn ab + bc + ca = 1. Chứng minh rằng: A = ( 2 + a )( 2 + b )( 2 1 1 1+ c ) là một số chính phương. Hướng dẫn: 3 2 2
x + x + x +1 = 0 ⇔ (x +1)(x +1) = 0 1. Với y = 0 => 2 + = + > ∀ <=> (x 1) 0 (Do : x 1 0 x) <=> x = -1. ≠
Với y 0 => y.y2 = (x + 1)(x2 + 1) y = x +1 2 2 ∈ℤ ⇒ < + < + => x, y y y , x 1 x 1) 2 2 y = x +1 (Vì: 2 2 2 2
(x +1) = x +1 ⇔ x + 2x +1= x +1⇔ x = 0 => y = 1
Vậy pt có nghiệm là: (x;y) = (-1; 0) ; (0; 1)
2. Vì: ab+bc+ca = 1 => 1 + a2 = ab+bc+ca + a2 = (a+b)(a+c) (1)
Tương tự: 1 + b2 = ab+bc+ca + b2 = (a+b)(b+c) (2)
1 + c2 = ab+bc+ca + c2 = (c+b)(a+c) (3)
Từ (1), (2) và (3) => A = (a+b)2(b+c)2(c+a)2 => A là số CP (ñpcm)