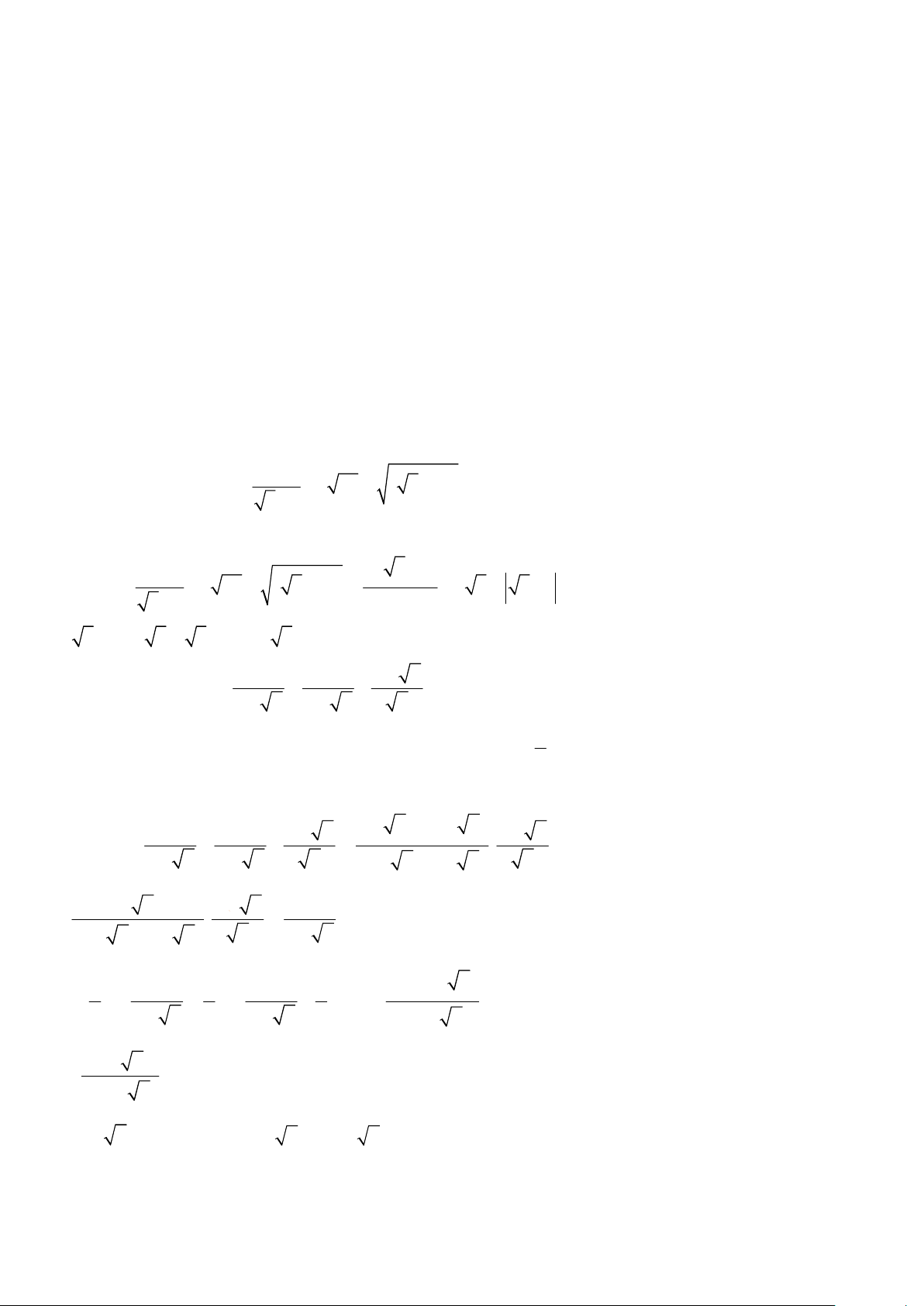

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT HÀ NAM NĂM HỌC 2019 - 2020 ------------ MÔN THI: TOÁN ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề) --------------------- Câu I (2,0 ñiểm). 1) Giải phương trình 2 x − 5x + 4 = 0 3 x − y = 3
2) Giải hệ phương trình: 2x + y = 7 Câu II (2,0 ñiểm).
1) Rút gọn biếu thức: A = − + ( − )2 4 3 45 5 1 5 −1 1 1 3 + x
2) Cho biểu thức: B = − .
, (với x > 0; x ≠ 9 ). 3 − x 3 + x x 1
Rút gọn biểu thức và tìm tất cả các giá trị nguyên của x ñể B > . 2
Câu III (1.5 ñiểm). 1
Trong mặt phẳng tọa ñộ Oxy cho parabol ( P) có phương trình 2 y =
x và ñường thẳng (d ) có phương 2
trình y = −mx + 3 − m (với m là tham số).
1) Tìm tọa ñộ ñiểm M thuộc parabol ( P) , biết ñiểm M có hoành ñộ bằng 4.
2) Chứng minh ñường thẳng (d ) luôn cắt parabol ( P) tại hai ñiểm phân biệt. Gọi x , x lần lượt là hoành ñộ 1 2 của hai ñiểm , A B . Tìm m ñể 2 2
x + x = 2x x + 20 . 1 2 1 2 Câu IV (4.0 ñiểm).
1) Cho nửa ñường tròn ( ;
O R) ñường kính AB . Trên cùng nửa mặt phẳng bờ AB chứa nửa ñường tròn ( ;
O R) vẽ các tiếp tuyến Ax, By với nửa ñường tròn ñó. Gọi M là một ñiểm bất kì trên nửa ñường tròn ( ;
O R) (với M khác A , M khác B ), tiếp tuyến của nửa ñường tròn tại M cắt Ax, By lần lượt tại C và D .
a) Chứng minh tứ giác ACMO nội tiếp.
b) Chứng minh tam giác COD vuông tại O . c) Chứng minh 2
AC.BD = R .
b) Kẻ MN ⊥ AB,( N ∈ AB) ; BC cắt MN tại I . Chứng minh I là trung ñiểm của MN .
2) Tính thể tích của một hình nón có bán kính ñáy r = 4 cm, ñộ dài ñường sinh l = 5 cm. Câu V (0,5 ñiểm).
Cho a, b, c là các số thực dương và thỏa mãn ñiều kiện abc = 1 1 1 1 Chứng minh + + ≤ 1. 2 + a 2 + b 2 + c Trang 1/5 - WordToan Hướng dẫn giải Câu I (2,0 ñiểm). 1) Giải phương trình 2 x − 5x + 4 = 0 Lời giải
Ta có a + b + c = 1 + ( 5
− ) + 4 = 0 ⇒ x = 1; x = 4 1 2
Vậy tập nghiệm của phương trình là S = {1; } 4 . 3 x − y = 3
2) Giải hệ phương trình: 2x + y = 7 Lời giải 3 x − y = 3 5 x = 10 x = 2 x = 2 Ta có ⇔ ⇔ ⇔ ⇒ ( ; x y) = (2;3) . 2x + y = 7 2x + y = 7 4 + y = 7 y = 3 Câu II (2,0 ñiểm).
1) Rút gọn biếu thức: A = − + ( − )2 4 3 45 5 1 5 −1 Lời giải + 2 4 5 1 4 Ta có A = − 3 45 + ( 5 − ) ( ) 1 = − 9 5 + 5 −1 5 −1 5 −1 = 5 +1− 9 5 + 5 −1 = 7 − 5 . 1 1 3 + x
2) Cho biểu thức: B = − .
, (với x > 0; x ≠ 9 ). 3 − x 3 + x x 1
Rút gọn biểu thức và tìm tất cả các giá trị nguyên của x ñể B > . 2 Lời giải 3 + x − + (3− 1 1 3 x x ) 3+ x Ta có B = − . = − x + x x ( − x)( + x). 3 3 3 3 x 2 x 3 + x 2 = ( = . 3 − x )(3 + x ) . x 3 − x 4 − (3 − 1 2 1 2 1 x ) B > ⇔ > ⇔ − > 0 ⇔ > 3 − x 3 − x 2 (3 − x ) 0 2 2 2 1 + ⇔ x > 2 (3 − x ) 0;(*) Vì 1+ x > 0 nên ( ) * ⇔ 3 − x > 0 ⇔
x < 3 ⇔ 0 < x < 9
Vì x ∈ ℤ ⇒ x ∈{1; 2;3; 4;5;6;7; } 8 .
Trang 2/5 – Diễn ñàn giáo viên Toán
Câu III (1.5 ñiểm). 1
Trong mặt phẳng tọa ñộ Oxy cho parabol ( P) có phương trình 2 y =
x và ñường thẳng (d ) có phương 2
trình y = −mx + 3 − m (với m là tham số).
1) Tìm tọa ñộ ñiểm M thuộc parabol ( P) , biết ñiểm M có hoành ñộ bằng 4. Lời giải 1 Vì M ∈ ( P) 2
⇒ y = .4 = 8 ⇒ M (4;8) . 2
2) Chứng minh ñường thẳng (d ) luôn cắt parabol ( P) tại hai ñiểm phân biệt. Gọi x , x lần lượt là hoành ñộ 1 2 của hai ñiểm , A B . Tìm m ñể 2 2
x + x = 2x x + 20 . 1 2 1 2 Lời giải 1
Phương trình hoành ñộ giao ñiểm của (d ) và ( P) là 2
x = −mx + 3 − m 2 2
⇔ x + 2mx + 2m − 6 = 0 2 2
Ta có ∆ = (−m) − ( m − ) 2 2
6 = m − 2m + 6 = (m − ) 1 + 5 > 0,∀m
Suy ra ñường thẳng (d ) luôn cắt parabol ( P) tại hai ñiểm phân biệt.
x + x = −2m Ta có hệ thức Vi-ét 1 2
x .x = 2m − 6 1 2 Yêu cầu 2 2 2 2
x + x = 2x x + 20 ⇔ x + x + 2x x = 4x x + 20 1 2 1 2 1 2 1 2 1 2
⇔ (x + x )2 = 4x x + 20 ⇔ ( 2
− m)2 = 4 2m − 6 + 20 1 2 1 2 ( )
⇔ m − m + = ⇔ (m − )2 2 4 8 4 0 4 1
= 0 ⇔ m −1 = 0 ⇔ m = (
1 thoa − man) . Vậy m = 1 . Câu IV (4.0 ñiểm).
1) Cho nửa ñường tròn ( ;
O R) ñường kính AB . Trên cùng nửa mặt phẳng bờ AB chứa nửa ñường tròn ( ;
O R) vẽ các tiếp tuyến Ax, By với nửa ñường tròn ñó. Gọi M là một ñiểm bất kì trên nửa ñường tròn ( ;
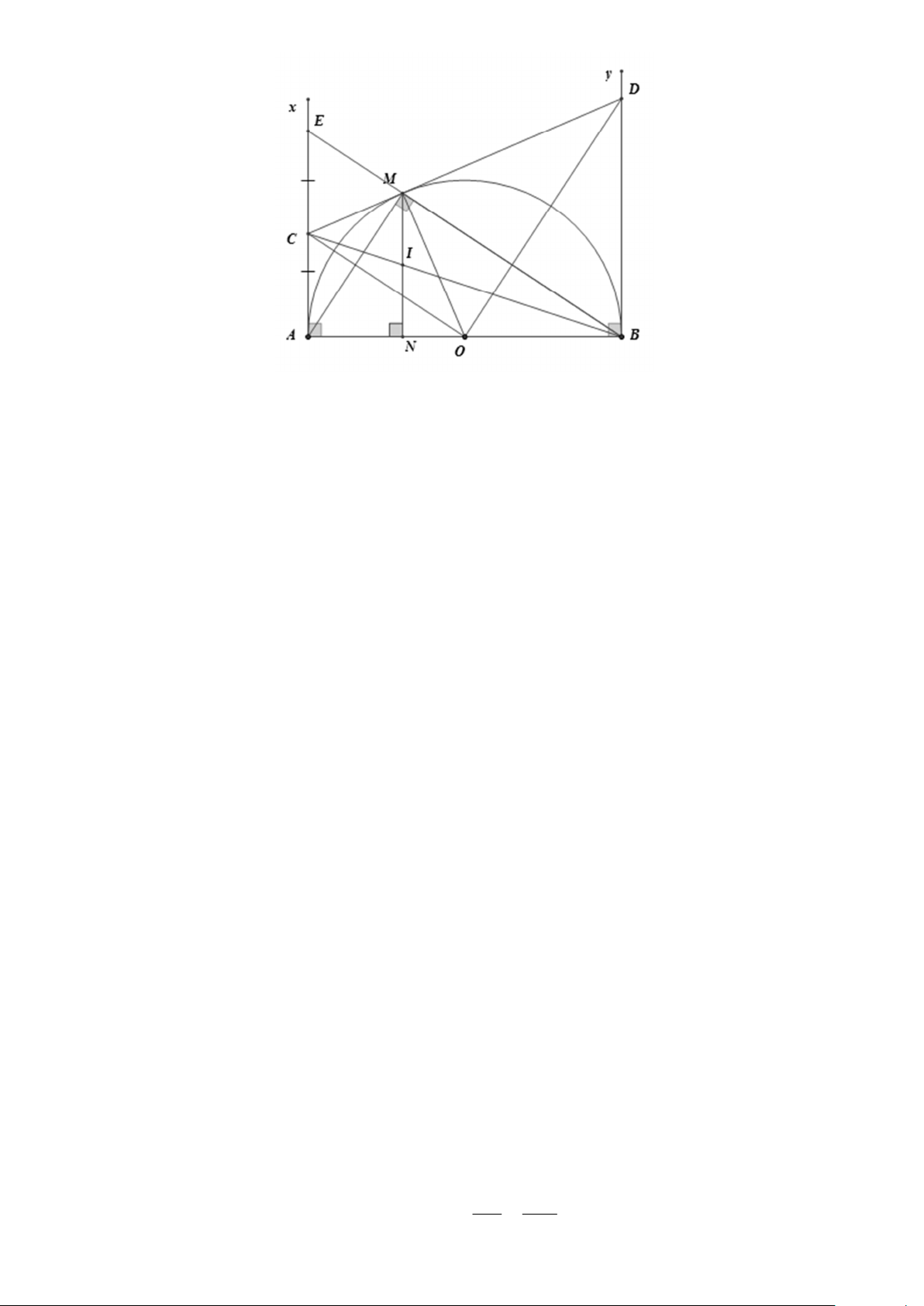
O R) (với M khác A , M khác B ), tiếp tuyến của nửa ñường tròn tại M cắt Ax, By lần lượt tại C và D .
a) Chứng minh tứ giác ACMO nội tiếp.
b) Chứng minh tam giác COD vuông tại O . c) Chứng minh 2
AC.BD = R .
b) Kẻ MN ⊥ AB,( N ∈ AB) ; BC cắt MN tại I . Chứng minh I là trung ñiểm của MN .
2) Tính thể tích của một hình nón có bán kính ñáy r = 4 cm, ñộ dài ñường sinh l = 5 cm. Lời giải Trang 3/5 - WordToan
a) Chứng minh tứ giác ACMO nội tiếp. OA ⊥ AC OAC = 90
Theo tính chất tiếp tuyến ta có ⇒ OM ⊥ CM OMC = 90
Xét tứ giác ACMO có tổng hai góc ở vị trí ñối nhau OAC + OMC = 90 + 90 = 180
Suy ra tứ giác ACMO nội tiếp.
b) Chứng minh tam giác COD vuông tại O .
Tương tự ý a) ta cũng chứng minh ñược tứ giác BDMO nội tiếp. Ta có
AMB = 90 (góc nội tiếp chắn nửa ñường tròn) suy ra tam giác ABM vuông tại B . Suy ra OAM + OBM = 90 Lại có OAM =
MCO (cùng chắn cung MO của ñường tròn ngoại tiếp tứ giác ACMO ) ODM =
OBM (cùng chắn cung MO của ñường tròn ngoại tiếp tứ giác BDMO ) DCO + ODC = MCO + ODM = OAM +
OBM = 90 ⇒ ∆ COD vuông tại O . c) Chứng minh 2
AC.BD = R . AC = MC
Theo tính chất hai tiếp tuyến cắt nhau ta có D B = MD
Tam giác COD vuông tại O có ñường cao OM
Áp dụng hệ thức lượng tam giác vuông ta có 2 2
MC.MD = OM ⇔ AC.BD = R ⇒ ðpcm.
d) Kẻ MN ⊥ AB,( N ∈ AB) ; BC cắt MN tại I . Chứng minh I là trung ñiểm của MN . Kẻ BM cắt Ax tại E.
Theo tính chất hai tiếp tuyến cắt nhau ta có CO là ñường phân giác trong của tam giác cân ACM. Suy ra OC
vừa phân giác vừa là ñường cao của tam giác ACM.
Suy ra OC ⊥ AM , mà EB ⊥ AM ⇒ OC // EB .
Lại có O là trung ñiểm của AB suy ra OC là ñường trung bình tam giác ABE.
Suy ra C là trung ñiểm của AE.
Ta có AE // MN (vì cùng vuông góc với AB). BA AE
Áp dụng hệ quả ñịnh lý Ta Lét vào tam giác ABE ta có = BN NM
Trang 4/5 – Diễn ñàn giáo viên Toán BA AC
Áp dụng hệ quả ñịnh lý Ta Lét vào tam giác ABC ta có = BN NI E A AC BA AE AC AE ⇒ = = ⇒ = ⇒
= NM = 2 ⇒ I là trung ñiểm của MN . NM NI BN NM NI AC NI
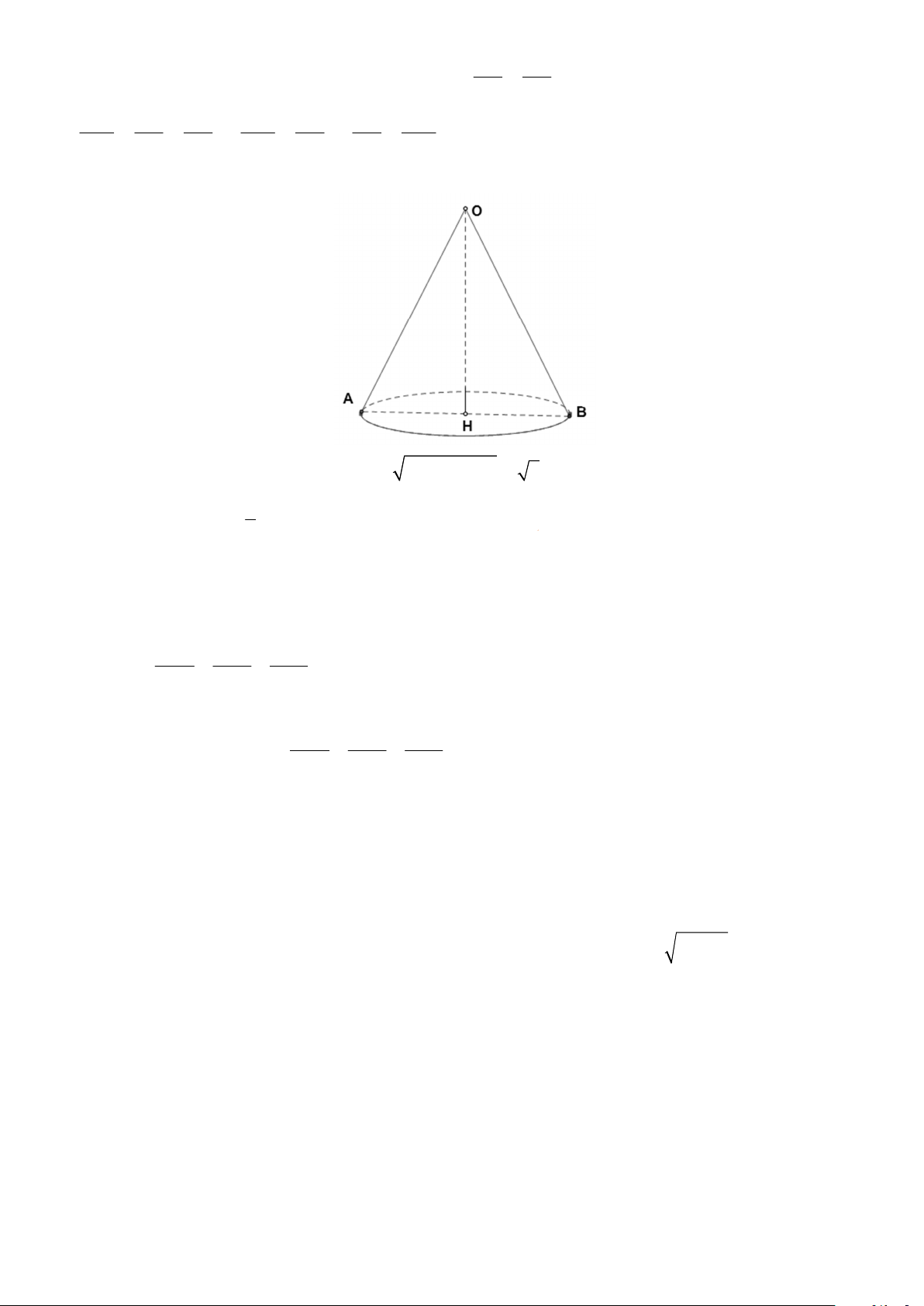
2) Tính thể tích của một hình nón có bán kính ñáy r = 4 cm, ñộ dài ñường sinh l = 5 cm. Ta có 2 2
AH = r = 4cm; AO = l = 5cm ⇒ OH = AO − AH = 9 = 3cm 1 Thể tích hình nón là 2 V = .OH.π .r = 16π ( 3 cm ). 3 Câu V (0,5 ñiểm).
Cho a, b, c là các số thực dương và thỏa mãn ñiều kiện abc = 1 1 1 1 Chứng minh + + ≤ 1. 2 + a 2 + b 2 + c Lời giải 1 1 1
Bất ñẳng thức cần chứng minh + + ≤ 1 2 + a 2 + b 2 + c
⇔ (b + 2)(c + 2) + (a + 2)(c + 2) + (a + 2)(b + 2) ≤ (a + 2)(b + 2)(c + 2)
⇔ ab + bc + ca + 4(a + b + c) +12 ≤ abc + 2(ab + bc + ca) + 4(a + b + c) + 8
⇔ ab + bc + ca + 4(a + b + c) +12 ≤ 1+ 2(ab + bc + ca) + 4(a + b + c) + 8
⇔ ab + bc + ca ≥ 3
Thật vậy áp dụng bất ñẳng thức CauChy cho 3 số dương ta có ⇔ ab + bc + ca ≥ (abc)2 3 3 ≥ 3 .
Dấu “=” xảy ra khi a = b = c = 1. Hoàn tất chứng minh. Trang 5/5 - WordToan




