

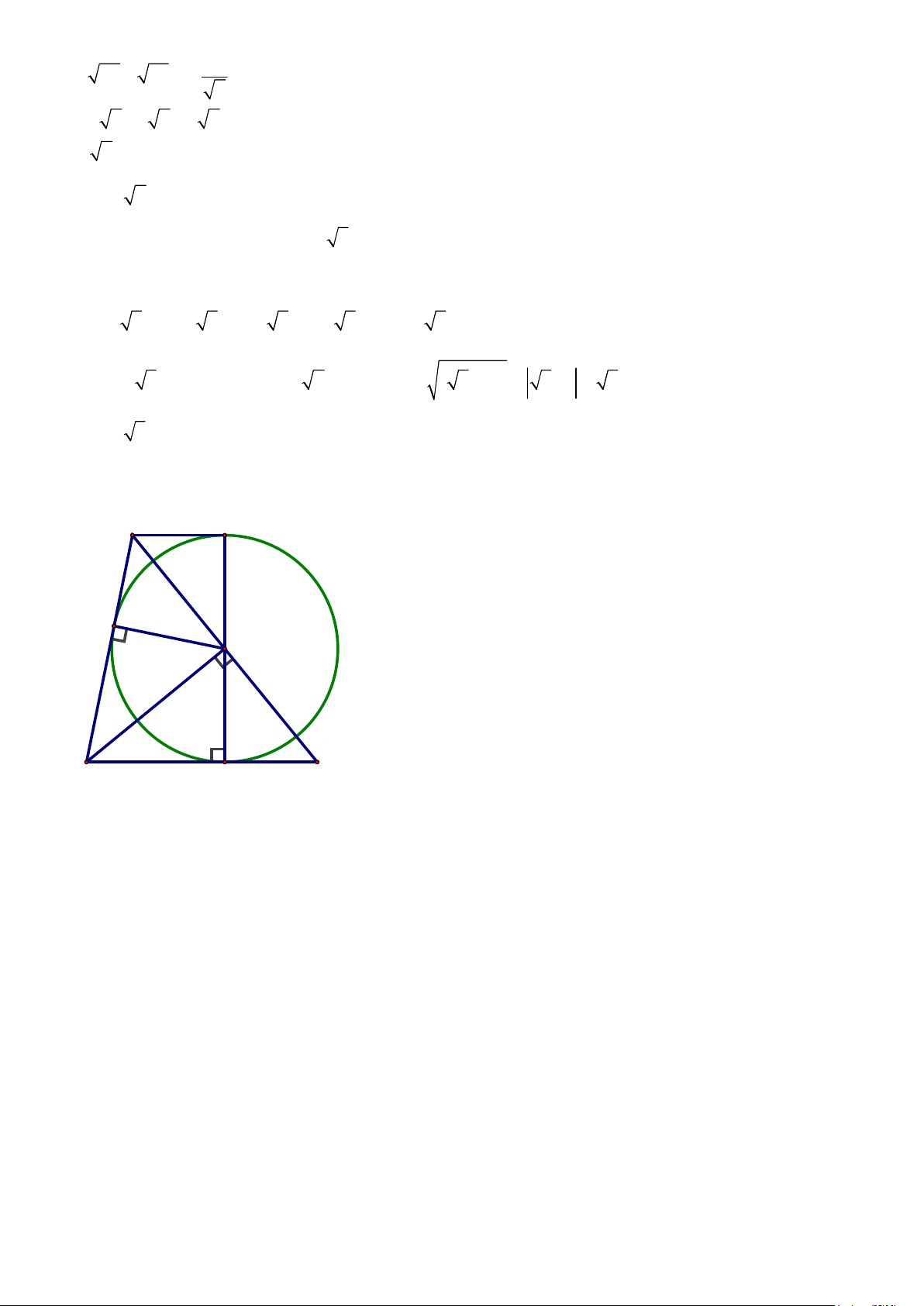


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT KHÁNH HÒA
Năm học 2019 – 2020 ------------------ Môn thi : TOÁN ĐỀ THI CHÍNH THỨC Ngày thi: 04/06/2019
Thời gian làm bài: 120 phút, không kể thời gian phát ñề
Bài 1: (2 ñiểm) Giải phương trình và hệ phương trình sau (không dùng máy tính cầm tay) 4 2 a) x + 3x − 4 = 0 x + 2y = 5 b)
x −5y = −9
Bài 2: (1,0 ñiểm) Trên mặt phẳng tọa ñộ Oxy, cho ñiểm T ( 2 − ; 2
− ) , parabol (P) có phương trình 2
y = −8x và ñường thẳng d có phương trình y = −2x − 6 .
a) ðiểm T có thuộc ñường thẳng d không?
b) Xác ñịnh tọa ñộ giao ñiểm của ñường thẳng d và parabol ( P) x
Bài 3: (2,0 ñiểm) Cho biểu thức P = 4x − 9x + 2 với x > 0 x a) Rút gọn P
b) Tính giá trị của P biết x = 6 + 2 5 (không dùng máy tính cầm tay).
Bài 4: (3,0 ñiểm) Cho tam giác ABC vuông tại A , ñường cao AH . Vẽ ñường tròn ( A) bán kính AH .
Từ ñỉnh B kẻ tiếp tuyến BI với ( A) cắt ñường thẳng AC tại D (ñiểm I là tiếp ñiểm, I và H không trùng nhau).
a) Chứng minh AHBI là tứ giác nội tiếp.
b) Cho AB = 4cm, AC = 3c . m Tính AI .
c) Gọi HK là ñường kính của ( A) . Chứng minh rằng BC = BI + DK .
Bài 5: (2,0 ñiểm) a) Cho phương trình 2
2x − 6x + 3m + 1 = 0 (với m là tham số). Tìm các giá trị của m ñể phương
trình ñã cho có hai nghiệm x , x thỏa mãn: 3 3 x + x = 9 1 2 1 2
b) Trung tâm thương mại VC của thành phố NT có 100 gian hàng. Nếu mỗi gian hàng của
Trung tâm thương mại VC cho thuê với giá 100.000.000 ñồng (một trăm triệu ñồng) một năm
thì tất cả các gian hàng ñều ñược thuê hết. Biết rằng, cứ mỗi lần tăng giá 5% tiền thuê mỗi gian hàng một
năm thì Trung tâm thương mại VC có thêm 2 gian hàng trống.
Hỏi người quản lý phải quyết ñịnh giá
thuê mỗi gian hàng là bao nhiêu một năm ñể doanh thu của Trung tâm thương mại VC từ tiền cho thuê gian
hàng trong năm là lớn nhất? ðáp án Bài 1: a) ðặt 2
x = t (t ≥ 0) , phương trình trở thành 2
t + 3t − 4 = 0.
Nhận xét: Phương trình có các hệ số a = 1, b = 2, c = −4 và a + b + c = 1+ 3 + (−4) = 0
Do ñó phương trình có hai nghiệm phân biệt t = 1(tm) 1 t = −4(ktm) 2 Với 2
t = 1 ⇒ x = 1 ⇔ x = ±1 1
Vậy tập nghiệm của phương trình là S = { 1 − ; } 1 x + 2y = 5 7 y = 14 y = 2 y = 2 b) ⇔ ⇔ ⇔ x − 5 y = −9 x = 5 − 2 y x = 5 − 2.2 x = 1
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = (1; 2) Bài 2:
a) ðiểm T có thuộc ñường thẳng d không?
Thay x = −2; y = −2 vào phương trình ñường thẳng d : y = −2x − 6 ta ñược −2 = −2.(−2) − 6 ⇔ 2 − = 2
− (luôn ñúng) nên ñiểm T thuộc ñường thẳng d.
b) Xác ñịnh tọa ñộ giao ñiểm của ñường thẳng d và parabol ( P) .
Xét phương trình hoành ñộ giao ñiểm của ñường thẳng d và parabol ( P) , ta có: 2 2 8 − x = 2
− x − 6 ⇔ 8x − 2x − 6 = 0 (*)
Phương trình (*) có a = 8;b = 2 − ;c = 6
− ⇒ a + b + c = 8 + ( 2 − ) + ( 6
− ) = 0 nên có hai nghiệm c 3 − x = 1; x = = 1 2 a 4 +Với 2
x = 1 ⇒ y = −8.1 = 8 − 2 3 3 9 + Với x = − ⇒ y = −8. − = − 4 4 2
Vậy tọa ñộ giao ñiểm của ñường thẳng d và parabol ( P) là ( − ) 3 9 1; 8 ; − ; − 4 2 Bài 3: a) Rút gọn P Với x > 0 thì: x
P = 4x − 9x + 2. x
= 2 x − 3 x + 2 x = x Vậy P =
x với x > 0 .
b) Tính giá trị của P biết x = 6 + 2 5 Ta có: x = + = + + = ( )2 + + = ( + )2 2 6 2 5 5 2 5 1 5 2. 5.1 1 5 1 Thay x = ( + )2
5 1 (tm) vào P =
x ta ñược P = ( + )2 5 1 = 5 +1 = 5 +1. Vậy P = 5 +1. Bài 4: D K I A B H C
a) Chứng minh tứ giác AHBI là tứ giác nội tiếp.
Do BI là tiếp tuyến của ( A) ⇒ ⊥ ⇒ 0 BI AI AIB = 90
Xét tứ giác AHBI có: 0 AIB = 90 0 AHB = 90 ( AH ⊥ BC) ⇒ + 0 0 0 AIB AHB = 90 + 90 = 180
⇒ Tứ giác AHBI là tứ giác nội tiếp ñường tròn ñường kính AB (tứ giác có tổng hai góc ñối bằng 0 180 )
b) Áp dụng hệ thức lượng trong tam giác vuông tính AH, suy ra AI.
Áp dụng hệ thức lượng trong tam giác vuông ABC, ñường cao AH ta có: 1 1 1 1 1 1 1 25 = + = + = + = 2 2 2 2 2 AH AB AC 4 3 16 9 144 144 144 12 2 ⇒ AH = ⇒ AH = = 25 25 5 12 Vậy AI = AH = (= R). 5
c) Gọi HK là ñường kính của ( A) . Chứng minh rằng BC = BI + DK . BI = BH ( ) 1
+) Áp dụng tính chất hai tiếp tuyến cắt nhau ta có: = BAI BAH = 0 ⇔ − 0 = − ⇔ = BAI BAH 90 BAI 90 BAH IAD HAC. Mà = ⇒ = HAC KAD IAD KA . D
+) Xét ∆ADI và ∆ADK có: AD chung = IAD KAD (cmt )
AI = AK (= R) Suy ra A ∆ DI = A ∆ KI ( . c g.c) ⇒ = 0 AKD
AID = 90 (hai góc tương ứng) ⇒ A
∆ KD vuông tại K.
+) Xét tam giác vuông AKD và tam giác vuông AHC có:
AK = AH (= R) ; = KAD HAC (ñối ñỉnh); A ∆ KD = A
∆ HC (cạnh góc vuông – góc nhọn kề)
⇒ DK = HC (2) (hai cạnh tương ứng). Từ ( )
1 và (2) suy ra BC = BH + HC = BI + DK (dpcm). Bài 5: a) 2
2x − 6x + 3m +1 = 0
Phương trình ñã cho có hai nghiệm ⇔ ∆ ' ≥ 0 2 ⇔ 3 − 2.(3m + ) 1 ≥ 0
⇔ 9 − 6m − 2 ≥ 0 ⇔ 7 − 6m ≥ 0 7 ⇔ m ≤ . 6
Khi ñó phương trình có hai nghiệm x ; x : 1 2 b x + x = − = 3 1 2 a
Theo ñinh lí Vi-et ta có: c 3m +1 x .x = = 1 2 a 2 Ta có :
x + x = 9 ⇔ ( x + x )3 3 3
− 3x x x + x = 9 1 2 1 2 1 2 ( 1 2 ) 3m +1 9 3 ⇒ 3 − 3. .3 = 9 ⇔ 27 − (3m + ) 1 − 9 = 0 2 2 27 27 ⇔ −
m = 0 ⇔ m = 1(TM ) 2 2
Vậy m = 1 thỏa mãn bài toán.
b) Gọi giá tiền mỗi gian hàng tăng lên x (triệu ñồng) (ðK: x > 0 )
Khi ñó giá mỗi gian hàng sau khi tăng lên là 100 + x (triệu ñồng).
Cứ mỗi lần tăng 5% tiền thuê mỗi gian hàng (tăng 5%.100 = 5 triệu ñồng) thì có thêm 2 gian hàng trống nên 2x
khi tăng x triệu ñồng thì có thêm gia hàng trống. 5 2x
Khi ñó số gian hàng ñược thuê sau khi tăng giá là 100 − (gian). 5
Số tiền thu ñược là: ( + x) 2x 100 100 − (triệu ñồng). 5
Yêu cầu bài toán trở thành tìm x ñể P = ( + x) 2x 100 100 −
ñạt giá trị lớn nhất. 5 Ta có: 2 P = ( + x) 2x 2x 100 100 − = 10000 − 40x +100x − 5 5 2 = − ( 2 2 2
x −150x ) +10000 = − ( 2 2 x − 2.75x + 75 ) 2 + .75 +10000 5 5 5 2
= − ( x − 75)2 +12250 5 2 2 2 2 2
Ta có ( x − 75) ≥ 0 ⇔ − ( x − 75) ≤ 0 ⇔ − ( x − 75) +12250 ≤ 12250 5 5
Dấu " = " xảy ra khi và chỉ khi x = 75 .
Vậy người quản lí phải cho thuê mỗi gian hàng với giá 100 + 75 = 175 triệu ñồng thì doanh thu của trung tâm
thương mại VC trong năm là lớn nhất.




