Đề tuyển sinh lớp 10 THPT năm 2019 – 2020 môn Toán sở GD&ĐT Lai Châu

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT LAI CHÂU NĂM HỌC 2019 - 2020 -------------- MÔN THI: TOÁN ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề) --------------------- Câu 1: (2,0 ñiểm)
1) Rút gọn các biểu thức sau: a) 3 4 + 2 25 − 4 9 b) 3 3 + 5 12 − 2 27
2) Giải phương trình và hệ phương trình sau: x + y = 2 a) 2 x − 6x + 5 = 0 b) 2x − y =  1 1 1 x
Câu 2: (1,5 ñiểm) Cho biểu thức M = + − x − 2 x + 2 4 − x
1) Tìm các giá trị thực của x ñể biểu thức có nghĩa? 2) Rút gọn biểu thức.
3) Tính giá trị của M biết x = 16 Câu 3: (2,5 ñiểm)
1) Quãng ñường AB dài 60km, một người ñi xe ñạp từ A ñến B với vận tốc và thời gian quy ñịnh.
Sau khi ñi ñược nửa quãng ñường người ñó giảm vận tốc 5km/h trên nửa quãng ñường còn lại. Vì
vậy, người ñó ñã ñến B chậm hơn quy ñịnh 1 giờ. Tính vận tốc và thời gian quy ñịnh của người ñó. 2) Cho phương trình: 2
2x + (2m −1)x + m −1 = 0 (1) trong ñó m là tham số.
a) Giải phương trình (1) khi m = 2 .
b) Tìm m ñể phương trình (1) có hai ngiệm thỏa mãn: 2 2
4x + x + x x = 1 4 2 2 1 2 1 Câu 4: (3,0 ñiểm)
Cho ñường tròn (O; R), dây BC cố ñịnh. ðiểm A di ñộng trên cung lớn BC (AB < AC) sao cho tam
giác ABC nhọn. Các ñường cao BE, CF cắt nhau tại H. Gọi K là giao ñiểm của EF với BC.
1) Chứng minh: Tứ giác BCEF nội tiếp. 2) Chứng minh: K . B KC = K . E KF
3) Gọi M là giao ñiểm của AK với (O) (M ≠ )
A . Chứng minh MH ⊥ AK .
Câu 5: (1,0 ñiểm) Cho các số thực dương a, b, c. Chứng minh rằng: ab bc ca 1 + +
≤ (a + b + c)
a + b + 2c
b + c + 2a
c + a + 2b 4
LỜI GIẢI ðỀ TUYỂN SINH VÀO 10 LAI CHÂU NĂM HỌC 2019-2020 Câu 1: (2,0 ñiểm)
1) Rút gọn các biểu thức sau: a) 3 4 + 2 25 − 4 9 b) 3 3 + 5 12 − 2 27
2) Giải phương trình và hệ phương trình sau: x + y = 2 a) 2 x − 6x + 5 = 0 b) 2x − y =  1 Lời giải
1) a) 3 4 + 2 25 − 4 9 = 3.2 + 2.5 − 4.3 = 4
b) 3 3 + 5 12 − 2 27 = 3 3 + 5.2 3 − 2.3 3 = 3 3 +10 3 − 6 3 = 7 3 2) a) 2 2
x − 6x + 5 = 0 ⇔ x − 5x − x + 5 = 0 ⇔ x(x − 5) − (x − 5) = 0 x − 5 = 0 x = 5
⇔ (x − 5)(x −1) = 0 ⇔ ⇔   x −1 = 0 x =   1 x + y = 2 3  x = 3 x = 1 x = 1 b)  ⇔  ⇔  ⇔  2x − y = 1 y = 2 − x y = 2 −1 y =     1
Vậy hệ ñã cho có nghiệm (x; y) là (1;1) 1 1 x
Câu 2: (1,5 ñiểm) Cho biểu thức M = + − x − 2 x + 2 4 − x
1) Tìm các giá trị thực của x ñể biểu thức có nghĩa?
2) Rút gọn biểu thức.
3) Tính giá trị của M biết x = 16 Lời giải
1) Tìm các giá trị thực của x ñể biểu thức có nghĩa? x ≥ 0   x − 2 ≠ 0 x ≥ 0 ðiều kiện:  ⇔  (*)  2 0 x x ≠ + ≠  4 4 − x ≠  0
Vậy x ≥ 0, x ≠ 0 thì biểu thức M có nghĩa.
2) Rút gọn biểu thức.
ðiều kiện: x ≥ 0 và x ≠ 4 1 1 = + − x M x − 2 x + 2 4 − x x + 2 x − 2 x = + +
( x − 2)( x + 2)
( x − 2)( x + 2)
( x − 2)( x + 2)
x + 2 + x − 2 + x 2 x + x x ( x + 2) x = = = =
( x − 2)( x + 2)
( x − 2)( x + 2)
( x − 2)( x + 2) x − 2 Vậy = x M x − 2
3) Tính giá trị của M biết x = 16
ðiều kiện: x ≥ 0 và x ≠ 4 16 4
Với x = 16 thì M = = = 2 16 − 2 4 − 2
Vậy với x = 16 thì M = 2. Câu 3: (2,5 ñiểm)
1) Quãng ñường AB dài 60km, một người ñi xe ñạp từ A ñến B với vận tốc và thời gian quy ñịnh.
Sau khi ñi ñược nửa quãng ñường người ñó giảm vận tốc 5km/h trên nửa quãng ñường còn lại. Vì
vậy, người ñó ñã ñến B chậm hơn quy ñịnh 1 giờ. Tính vận tốc và thời gian quy ñịnh của người ñó.
2) Cho phương trình: 2
2x + (2m −1)x + m −1 = 0 (1) trong ñó m là tham số.
a) Giải phương trình (1) khi m = 2 .
b) Tìm m ñể phương trình (1) có hai ngiệm thỏa mãn: 2 2
4x + x + x x = 1 4 2 2 1 2 1 Lời giải
1) Gọi vận tốc quy ñịnh của người ñó là x (km/h), (x > 5) 60
⇒ Thời gian quy ñịnh ñể người ñó ñi hết quãng ñường là (h). x 30
Nửa quảng ñường ñầu là: 60 : 2 = 30(km) nên thời gian ñi nửa quãng ñường ñầu là: (h) . x
Nửa quãng ñường sau, vận tốc của người ñó giảm 5km/h nên vận tốc lúc sau là: x − 5(km / h) . 30
⇒ Thời gian ñi nửa quãng ñường sau là (h) . x − 5
Vì người ñó ñến chậm so với thời gian dự ñịnh là 1 giờ nên ta có phương trình: 30 30 60 30 30 + −1 = ⇔ − −1 = 0 x x − 5 x x − 5 x
30x − 30(x − 5) − x(x − 5) ⇔ = 0 x(x − 5) 2
⇒ 30x − 30x +150 − x + 5x = 0 2
⇔ x − 5x −150 = 0 2
⇔ x −15x +10x −150 = 0
⇔ x(x −15) +10(x −15) = 0
⇔ (x −15)(x +10) = 0 x −15 = 0 x = 15 (tm) ⇔ ⇔   x + 10 = 0 x = −   10 (ktm)
Vậy vận tốc quy ñịnh của người ñó là 15km/h và thời gian quy ñịnh của người ñó là: 60 : 15 = 4 giờ.
2) Cho phương trình 2
2x + (2m −1)x + m −1 = 0 (1) trong ñó m là tham số.
a) Giải phương trình (1) khi m = 2 .
Khi m = 2 thì (1) trở thành: 2
2x + 3x +1 = 0 có hệ số a = 2;b = 3; c = 1 c 1
Dễ thấy a − b + c = 2 − 3 +1 = 0 nên phương trình có hai nghiệm x = − x = − = − 1 1; 2 a 2  1 
Vậy với m = 2 thì phưng trình có tập nghiệm S = −1; −   2 
b) Tìm m ñể phương trình (1) có hai ngiệm thỏa mãn: 2 2
4x + x + x x = 1 4 2 2 1 2 1
Phương trình (1) có nghiệm ⇔ ∆ ≥ 0 Ta có: 2 2 2 2
∆ = (2m −1) − 4.2.(m −1) = 4m − 4m +1−8m + 8 = 4m −12m + 9 = (2m − 3) Dễ thấy 2
∆ = (3m − 3) ≥ 0,∀m nên phương trình ñã cho luôn có hai nghiệm 1 x , 2 x  1− 2m 1 x + x2 =  2
Theo ñịnh lí Vi-ét ta có:  m −1  1xx2 =  2 Theo ñề bài ta có: 2 2 2 2
x + x + x x = ⇔ x + x + x x = ⇔  2 4 x + x −  x x + x x = 1 4 2 2 1 2 1 4( 1 2 ) 2 1 2 1 4 (  1 2 ) 2 1 2 2  1 2 1 2 2 ⇔ 4(x + x
− x x + x x = ⇔ x + x − x x = 1 2 ) 8 1 2 2 1 2 1 4( 1 2 ) 6 1 2 1 2  1− 2m  m −1 2 ⇒ 4 − 6.
= 1 ⇔ (2m −1) − 3(m −1) −1 =   0  2  2 m = 1 2 2 
⇔ 4m − 4m +1− 3m + 3 −1 = 0 ⇔ 4m − 7m + 3 = 0 ⇔ 3 m =  4  3  Vậy m ∈ 1
 ;  thỏa mãn bài toán.  4  Câu 4: (3,0 ñiểm)
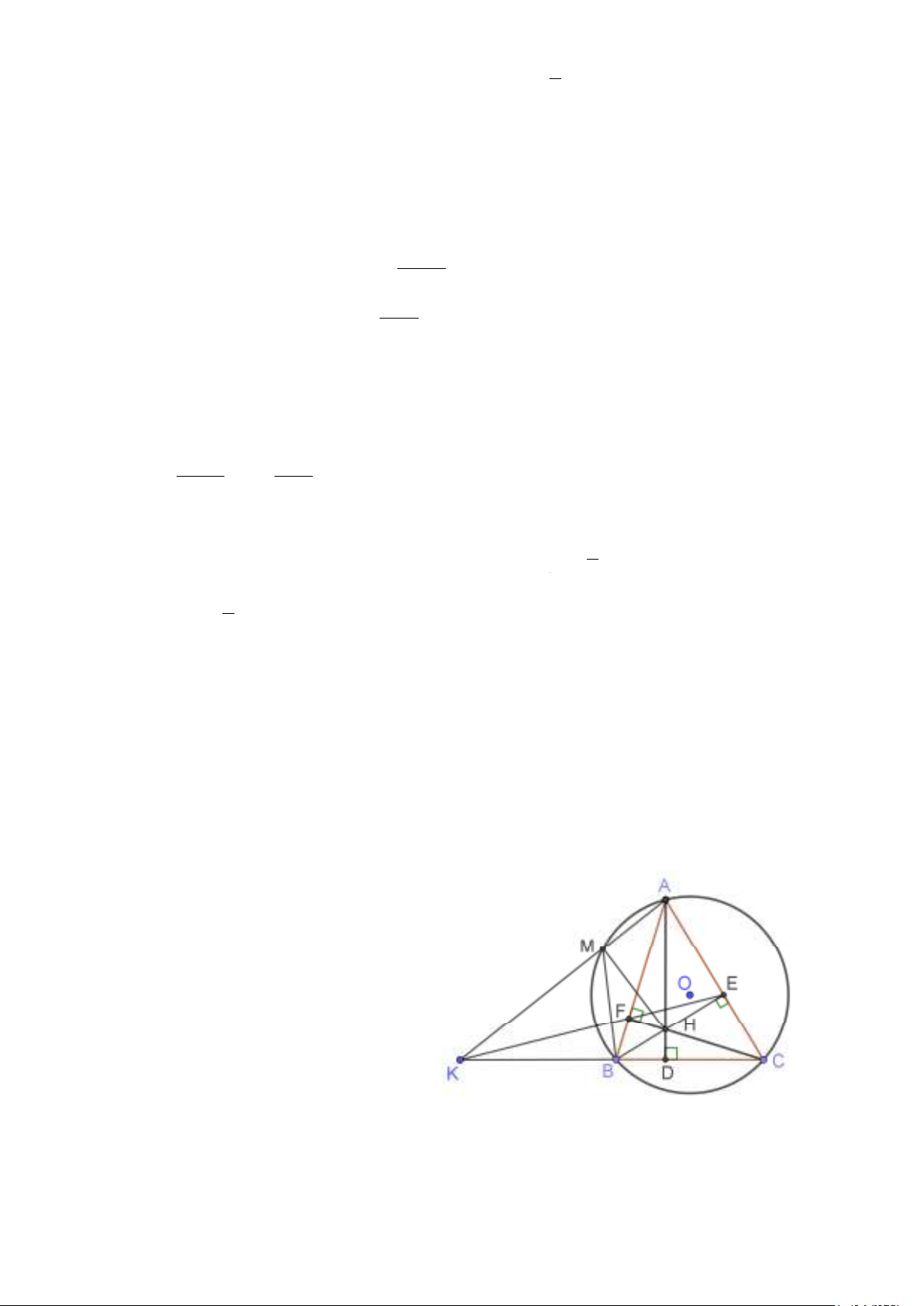
Cho ñường tròn (O; R), dây BC cố ñịnh. ðiểm A di ñộng trên cung lớn BC (AB < AC) sao cho tam
giác ABC nhọn. Các ñường cao BE, CF cắt nhau tại H. Gọi K là giao ñiểm của EF với BC.
1) Chứng minh: Tứ giác BCEF nội tiếp. 2) Chứng minh: K . B KC = K . E KF
3) Gọi M là giao ñiểm của AK với (O) (M ≠ )
A . Chứng minh MH ⊥ AK . Lời giải
1) Chứng minh: Tứ giác BCEF nội tiếp.
BE ⊥ AC ⇒ 0 BEC = 90 Do 
CF ⊥ AB ⇒ 0 CFB =  90 Tứ giác BCEF có BEC = 0 CFB =
90 nên là tứ giác nội tiếp (hai ñỉnh kề nhau cùng nhìn một cạnh
dưới các góc bằng nhau).
2) Chứng minh: K . B KC = K . E KF
Tứ giác BCEF nội tiếp (câu a) nên KFB =
ECB (góc ngoài tại một ñỉnh bằng góc trong tại ñỉnh ñối diện)
Xét tam giác ∆KFB và ∆KCE có:  K chung  ⇒ ∆KFB ∆KCE (g - g)  KFB =  KCE (cmt) ⇒ KF = KB ⇒ KF KE =
(các cặp cạnh tương ứng tỉ lệ) . K . B KC (ñpcm) KC KE
3) Gọi M là giao ñiểm của AK với (O) (M ≠ )
A . Chứng minh MH ⊥ AK .
Kéo dài AH cắt BC tại D thì AD ⊥ BC ⇒ 0 ADB = 90
Xét tam giác AFH và ADB có:   A chung AF AH  ⇒ A ∆ FH ∆ADB (g - g) ⇒ =
(các cặp cạnh tương ứng tỉ lệ)  H = 0 AF ADB = 90 AD AB
⇒ AF.AB = A . D AH (1)
Dễ thấy tứ giác AMBC nội tiếp (O) nên AMB + 0 ACB = 180 (tính chất) (2)
Tứ giác ABCF nội tiếp (cmt) nên BFE + 0 BCE = 180 Mà BFE = AFK (ñối ñỉnh) ⇒ AFK + 0 ACB = 180 (3) Từ (2) và (3) suy ra AMB = AFK (cùng bù với ACB )
Xét tam giác AMB và AFK có:   A chung AM AB  ⇒ A ∆ MB ∆AFK (g - g) ⇒ =
(các cặp cạnh tương ứng tỉ lệ)  = AMB AFK (cmt) AF AK ⇒ AM .AK = . AB AF (4) AM AD
Từ (1) và (4) suy ra AM AK = AD AH ⇒ = . . AH AK
Xét tam giác AMH và ADK có: A chung   ⇒ ∆ ∆ ⇒ AMH = AM AH AMH ADK (c - g - c)
ADK (hai góc tương ứng)  = (cmt)  AD AK Mà 0 ADK = ⇒ 0 90
AMH = 90 hay HM ⊥ AK (ñpcm)
Câu 5: (3,0 ñiểm) Cho các số thực dương a, b, c. Chứng minh rằng: ab bc ca 1 + +
≤ (a + b + c)
a + b + 2c
b + c + 2a
c + a + 2b 4 Lời giải 1 1  1 1 
Ta chứng minh bất ñẳng thức ≤ +   x + y 4  x
y  với x, y > 0.
Thậy vậy, với x, y > 0 thì: 1 1  1 1  1 x + y 2 2 2 ≤ + ⇔ ≤
⇔ (x + y) ≥ 4xy ⇔ x + 2xy + y − 4xy ≥   0 x + y 4 x y x +   y 4xy 2 2 2
⇔ x − 2xy + y ≥ 0 ⇔ (x − y) ≥ 0 (luôn ñúng) 1 1  1 1  Do ñó: ≤ +   x + y 4  x
y  với x, y > 0.
Áp dụng bất ñẳng thức trên ta có: 1 1 1 1 1 ab ab  1 1  = ≤ ( + ) ⇒ ≤ +  
a + b + 2c
(a + c) + (b + c) 4 a + c b + c
a + b + 2c
4 a + c b + c    bc bc  1 1  ≤ +   
b + c + 2a 4  b + a c + a  Tương tự ta có:  ca ca  1 1   ≤ +  
c + a + 2b 4  c + b a + b 
Cộng vế với vế các bất ñẳng thức với nhau ta ñược: ab bc ca ab  1 1  bc  1 1  ca  1 1  + + ≤ + + + + +      
a + b + 2c
b + c + 2a
c + a + 2b
4 a + c b + c  
4 b + a c + a  
4 c + b a + b   1  ab ab bc bc ca ca  = + + + + + 4   a + c b + c b + a c + a c + b a + b  
1 ab + bc ab + ca bc + ca  1  ( b a + c) ( a b + c) ( c b + a) 1 = + + = + +
= (a + b + c) 4     a + c c + b b + a   4 a + c c + b b + a   4 1 Do ñó VT ≤ VP (ñpcm). 4
Dấu “=” xảy ra khi a = b = c.