Đề tuyển sinh lớp 10 Toán (chuyên) 2022 – 2023 trường chuyên Lê Quý Đôn – BR VT

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN LÊ QUÝ ĐÔN TỈNH BÀ RỊA-VŨNG TÀU Năm học: 2022 – 2023 ĐỀ CHÍNH THỨC
ĐỀ THI MÔN: TOÁN (Chuyên)
Thời gian: 150 phút (không kể thời gian phát đề) Ngày thi:09/06/2022 Câu 1 (3,0 điểm).  x  2 x  2  2( x 1)
a) Rút gọn biểu thức P     : với x  0, x  1. 2 2 ( x 1)( x 1) ( x 1) (1 x)   b) Giải phương trình: 2
x  3x  2  (x 1) 2x  5  0 . 2 x  4xy  x  2  0
c) Giải hệ phương trinh:  . 2 4y  x  4y 1  0 Câu 2 (2,0 điểm). ac
a) Cho các số thực a,b,c, d thỏa mãn
 2 . Chứng minh phương trình sau luôn b  d có nghiệm  2 x  ax  b 2 x  cx  d   0
b) Tìm tất cả các cặp số nguyên (x; y) thỏa mãn phương trình 2
(x  y)(2x  3y)  2x  y  2  0 . Câu 3 (1,0 điểm).
Với các số thực dương x, y, z thỏa mãn  2 2 2
2 x  y  z   3y(x  z).
Tìm giá trị lớn nhất của biểu thức P  x  y  z   2 2 2( ) x  z  . Câu 4 (3,0 điểm).
Cho tam giác ABC nhọn (AB  AC) nội tiếp đường tròn tâm O và có ba đường cao
AD, BE,CF cắt nhau tại H . Gọi I , J lần lượt là trung điểm của AH và BC .
a) Chứng minh rằng IJ vuông góc với EF và IJ song song với OA .
b) Gọi K ,Q lần lượt là giao điểm của EF với BC và AD . Chứng minh rằng QE KE  . QF KF
c) Đường thẳng chứa tia phân giác của 
FHB cắt AB, AC lần lượt tại M và N . Tia phân giác của 
CAB cắt đường tròn ngoại tiếp tam giác AMN tại điểm P khác A .
Chứng minh ba điểm H , P, J thẳng hàng. Câu 5 (1,0 điểm).
Cho tam giác ABC cố định có diện tích S . Đường thẳng d thay đổi đi qua trọng
tâm của tam giác ABC cắt các cạnh AB, AC lần lượt tại M , N , Gọi S , S lần lượt là 1 2
diện tích các tam giác ABN và ACM . Tìm giá trị nhỏ nhất của S  S . 1 2
--------------HẾT------------- HƯỚNG DẪN GIẢI Câu 1 (3,0 điểm).  x  2 x  2  2( x 1)
a) Rút gọn biểu thức P     : với x  0, x  1. 2 2 ( x 1)( x 1) ( x 1) (1 x)   b) Giải phương trình: 2
x  3x  2  (x 1) 2x  5  0 . 2 x  4xy  x  2  0
c) Giải hệ phương trinh:  . 2 4y  x  4y 1  0 Lời Giải: 2 2
( x  2)( x 1)  ( x  2)( x 1) (x 1) (2 x )(x 1) a) P        x . 2 2 2 ( x 1)( x 1) 2( x 1) 2( x 1) ( x 1)   5 b) Điều kiện : x  . 2 x 1  0(1)
Phương trình  (x 1)(x  2  2x  5)  0   . x   2  2x  5(2)
(1)  x  1 (không thỏa mãn điều kiện). x  2 x  2 (2)      x  3. 2 2 (x  2)  2x  5  x  6x  9  0
Vậy tập hợp nghiệm của phương trình đã cho là S  {3}.
c) Cộng hai phương trình đã cho theo vế được x  2y 1 2
(x  2y)  2(x  2 y)  3  0   . x  2y  3 
Trường hợp 1: x  2y  1  x  1 2 y thay vào phương trình sau của hệ thu được  y  0  x  1 2 4 y 1 2 y 4 y 1 0        1  y    x  2  2
Trường hợp 2 : x  2 y  3  x  2y  3 thay vào phương trình sau của hệ thu được  1 17 5  17  y   x  2 2 4 2
4 y  3  2 y  4 y 1  0  2 y  y  2  0    1 17 5  17  y   x   4 2
Vậy hệ phương trình đã cho có 4 nghiệm    1   5   17 1   17   5   17 1   17  1;0 ; 2; ;    ; ; ;  . 2  2 4   2 4        Câu 2 (2,0 điểm). ac
a) Cho các số thực a,b,c, d thỏa mãn
 2 . Chứng minh phương trình sau luôn b  d có nghiệm  2 x  ax  b 2 x  cx  d   0
b) Tìm tất cả các cặp số nguyên (x; y) thỏa mãn phương trình 2
(x  y)(2x  3y)  2x  y  2  0 . Lời Giải: 2 x  ax  b  0(1)
a) Phương trình đã cho   . 2 x  cx  d  0(2) Ta có 2   a  4b và 2   c  4d 1 2
Giả sử phương trình này vô nghiệm, khi đó cả hai phương trình (1), (2) đều vô 2 (1)  0 4b  a nghiệm. Tức là   
 b  0;d  0  b  d  0 . 2 (2)  0  4d  c ac
Lúc này theo giả thiết thì  2  ac  2(b  d) . b  d 1
Tuy nhiên điều này vô lý do 2(b  d)   2 2 a  c   ac . 2
Vậy với điều kiện đề cho thì pt  2 x  ax  b 2
x  cx  d   0 luôn có nghiệm a  x  y b/ Đặt  b   2x  3y
Khi đó 2x  y  2  4x  4 y  2x  3y  2
 4x  y  2x  3y  2  4a  b  2 Ta có 2
(x  y)(2x  3y)  2x  y  2  0 2
 ab  4a  b  2  0  a  2 b  4  b  2 2  b  2b  4
 b  b   2 2 2 b  4   2
b    b  b   2 4 2 2 b  4   2 8 b  4   2 b  44,  8 1 Nếu 2
b  4  4  b  0  a   2  1 x  y     2 2x  3y  0  3 x     2 (loại) y 1 Nếu 2 b  4  4 b  2  a  0   1 b  2   a    2 *) b  2  a  0 x  y  0   2x  3y  2 x  2    (nhận) y  2 1 *) b  2   a   2  1 x  y     2 2x  3y  2  1 x    2 (loại) y  1  Vậy  2
 ;2 thỏa mãn pt đã cho Câu 3 (1,0 điểm).
Với các số thực dương x, y, z thỏa mãn  2 2 2
2 x  y  z   3y(x  z).
Tìm giá trị lớn nhất của biểu thức P  x  y  z   2 2 2( ) x  z  . Lời Giải: Ta có : 2 y x  z  y   2 2 x  z  2 2 3 ( ) 2 2  2 y  (x  z) 2 2
 3y(x  z)  2y  (x  z) 2 2
 (x  z)  3y(x  z)  2y  0 2  x  z   x  z    3  2  0      y   y  x  z  1  2 . y Do đó : 2 2 3  1   1  3 2 2 2 2 2 2
P  4(x  z)  x  z  2 x  z  x  z  x  z 1 x  z   x   z       2  2   2  2 . 1
Đẳng thức xảy ra  x  z  ; y  1. 2 3
Vậy giá trị lớn nhất của biểu thức P là . 2 Câu 4 (3,0 điểm).
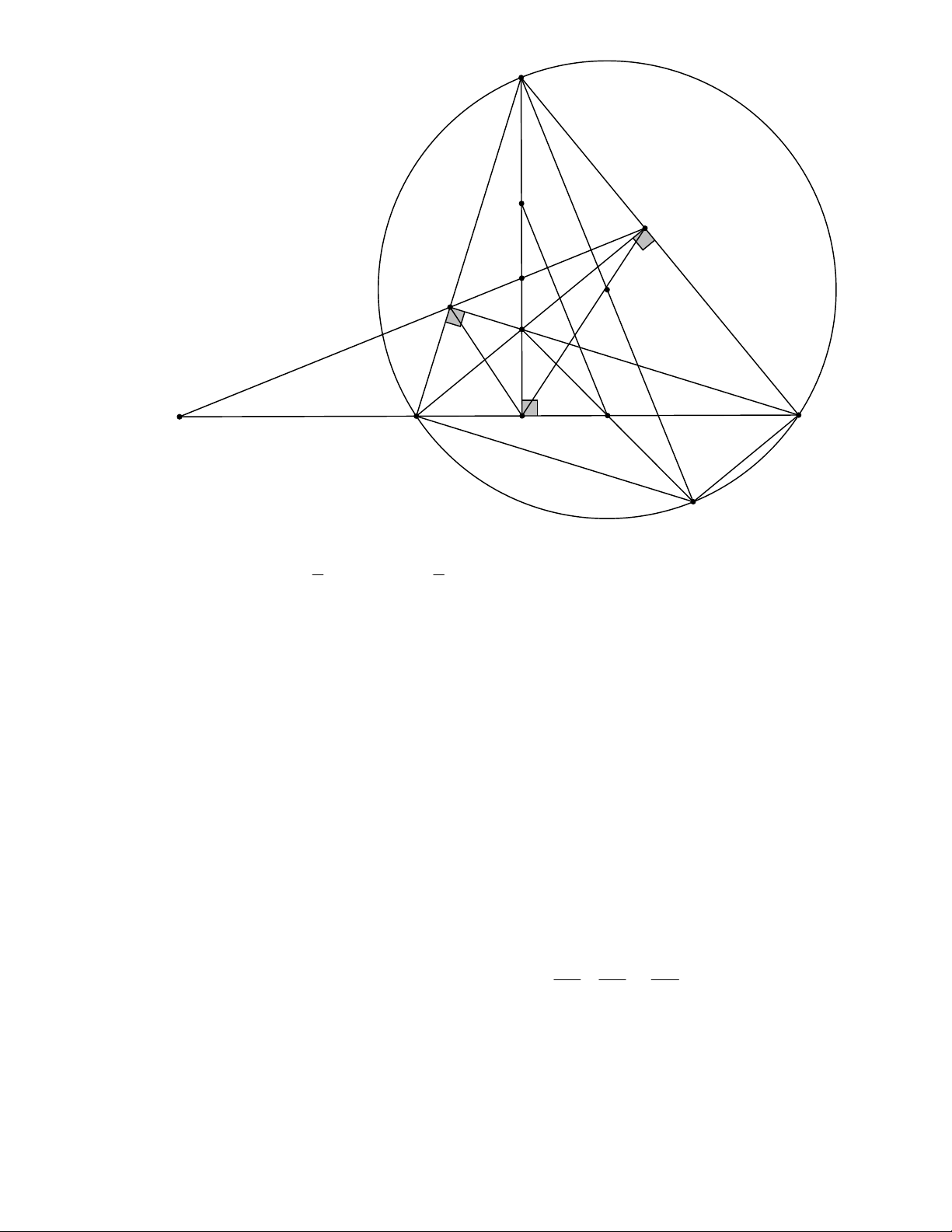
Cho tam giác ABC nhọn (AB  AC) nội tiếp đường tròn tâm O và có ba đường cao
AD, BE,CF cắt nhau tại H . Gọi I , J lần lượt là trung điểm của AH và BC .
a) Chứng minh rằng IJ vuông góc với EF và IJ song song với OA .
b) Gọi K ,Q lần lượt là giao điểm của EF với BC và AD . Chứng minh rằng QE KE  . QF KF
c) Đường thẳng chứa tia phân giác của 
FHB cắt AB, AC lần lượt tại M và N . Tia phân giác của 
CAB cắt đường tròn ngoại tiếp tam giác AMN tại điểm P khác A .
Chứng minh ba điểm H , P, J thẳng hàng. Lời Giải: A J E Q F O H K B D I C T 1 1
a) IE  IF  BC; JE  JF  AH 2 2
 IJ là đường trung trực của EF .  IJ  EF
Kẻ đường kính AT của (O)
 BHCT là hình bình hành
 I là trung điểm của HT .  IJ //AT
b) Các tứ giác BDHF,CDHE, BCEF là các tứ giác nội tiếp nên ta có  EDH   HCE   HBF   HDF
và do HD  HK  DQ, DK là phân giác trong và phân giác ngoài của tam giác DEF .
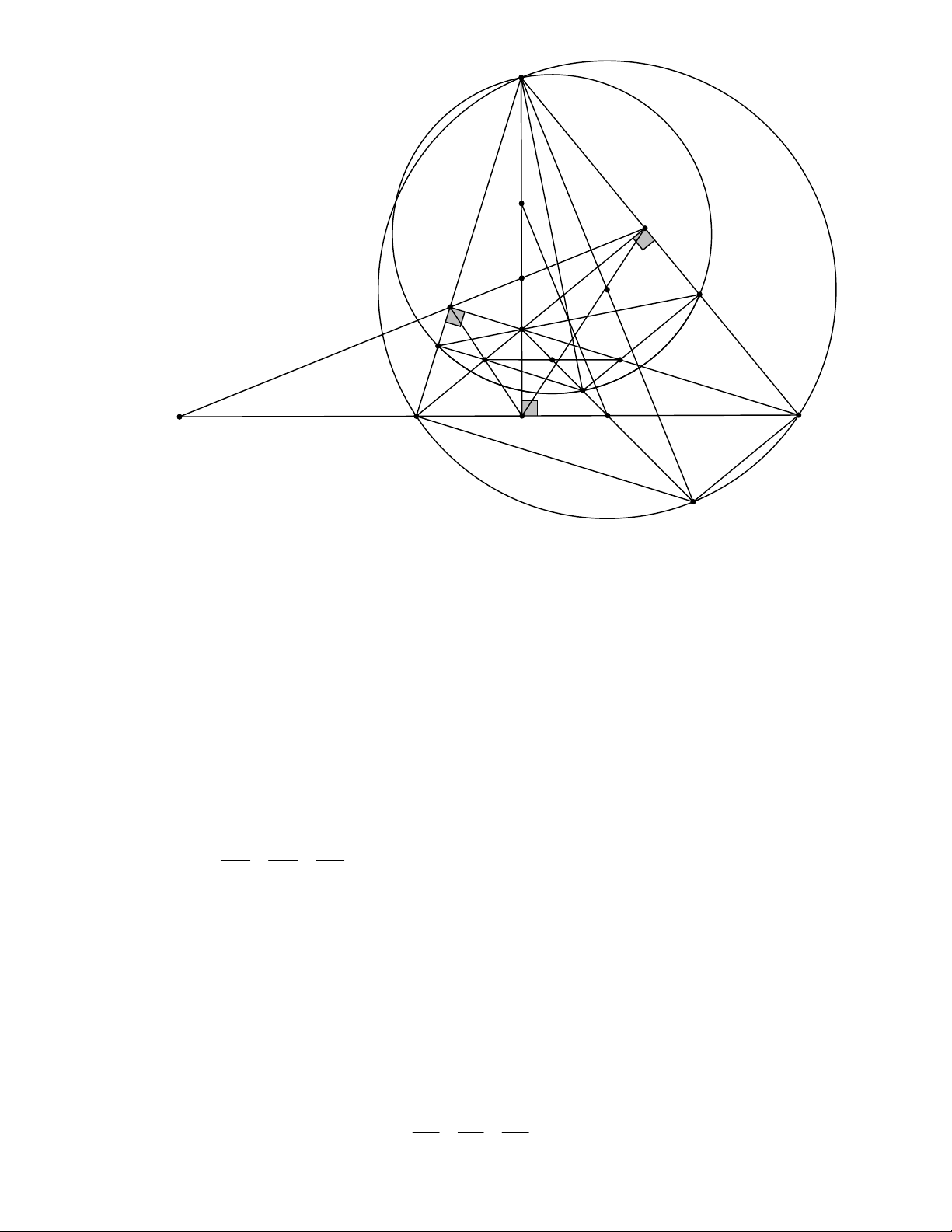
Đến đây theo tính chất đường phân giác thì QE KE  DE      . QF KF  DF  A J E Q O F N H G R L M P K B D I C T c) Ta có  AMH   MBH   MHB   NCH   NHC   HNA  A  MN cân tại A
 AP là đường kính của (AMN )  PM //HC, PN //HB .
Gọi G là giao điểm của PM , HB và L là giao điểm của PN , HC .
Khi đó tứ giác HGPL là hình bình hành
nên HP đi qua trung điểm R của GL .
Đến đây sử dụng định lý Talet và tính chất đường phân giác ta được GH MF HF   ; GB MB HB LH NE HE   . LC NC HC HF HE
Tuy nhiên hai tam giác HFB, HEC đồng dạng nên  . HB HC GH LH    GL//BC GB LC Cho HR cắt BC tại I RG AR RL
sử dụng định lý Talet thì   IB AI I C   IB  I C   I  I .
Vậy ba điểm H , P, I thẳng hàng. Câu 5 (1,0 điểm).
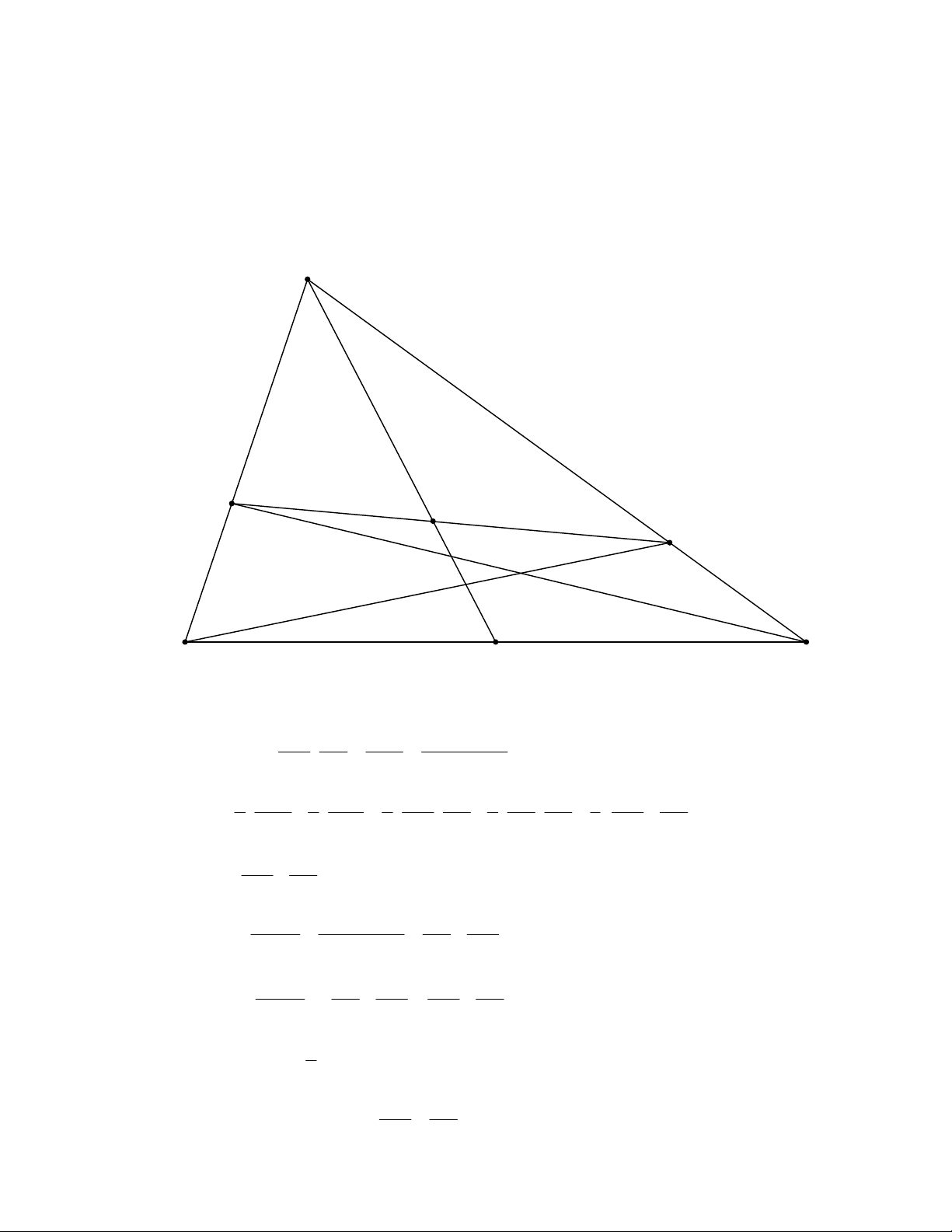
Cho tam giác ABC cố định có diện tích S . Đường thẳng d thay đổi đi qua trọng
tâm của tam giác ABC cắt các cạnh AB, AC lần lượt tại M , N , Gọi S , S lần lượt là 1 2
diện tích các tam giác ABN và ACM . Tìm giá trị nhỏ nhất của S  S . 1 2 Lời Giải: A M G N B C D
Gọi D là trung điểm BC và G là trọng tâm tam giác ABC . AM AN S S  S Ta có : AMN AMG ANG    AB AC S S 1 S 1 S 1 AM AG 1 AN AG 1  AM AN  AMG ANG               2 S 2 S 2 AB AD 2 AC AD 3  AB AC  ABD ACD AB AC    3 AM AN S  S S  S Mà AN AM 1 2 ABN ACM    S S AC AB ABC S  S  AN AM  AB AC  1 2  3.     4    S  AC AB  AM AN  4  S  S  S . 1 2 3 AM AN Đẳng thức xảy ra    d //BC . AB AC 4
Vậy giá trị nhỏ nhất của biểu thức S  S là S , đạt được khi và chỉ khi d //BC . 1 2 3