Đề tuyển sinh vào lớp 10 môn Toán năm 2021 – 2022 sở GD&ĐT Đắk Lắk

Giới thiệu đến quý thầy, cô giáo và các em học sinh đề tuyển sinh vào lớp 10 môn Toán năm học 2021 – 2022 sở GD&ĐT Đắk Lắk; đề thi có đáp án và lời giải chi tiết (lời giải được trình bày bởi thầy giáo Nguyễn Dương Hải – giáo viên Toán trường THCS Nguyễn Chí Thanh, Buôn Ma Thuộc, Đắk Lắk). Mời bạn đọc đón xem!

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

3 trang 8 tháng trước

Tác giả:

Profile Vũ Hường
trang
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐẮK LẮK
ĐỀ THI CHÍNH THỨC
KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG
NĂM HỌC 2021 - 2022
MÔN THI: TOÁN
(Thời gian 120 phút không kể thời gian phát đề)
Ngày thi 09/6/2021
Câu 1: (1,5 điểm)
1) Giải phương trình:
2
2 5 3 0x x .
2) Cho hàm số
1 2021y m x
. Tìm tất cả các giá trị của tham số m để hàm số
đồng biến trên
.
3) Cho 1 2a và 1 2b . Tính giá trị của biểu thức: 2P a b ab
Câu 2: (2,0 điểm) Cho biểu thức:
2 9 3 2 1
5 6 2 3
x x x
P
x x x x
với
0, 4, 9x x x
1) Rút gọn P .
2) Tìm các giá trị của
x
để 1P .
Câu 3: (2,0 điểm)
1) Trong mặt phẳng tọa độ Oxy, viết phương trình đường thẳng
đi qua điểm
1; 2A và song song với đường thẳng 2 1y x .
2) Trong mặt phẳng tọa độ
Oxy
cho Parabol
2
:
P y x
và đường thẳng
: 2 1 3d y m x m . Gọi
1 2
,x x là hoành độ giao điểm của đường thẳng
d và
Parabol
P
. Tìm giá trị nhỏ nhất của
2 2
1 2
M x x .
Câu 4: (3,5 điểm)
Trên nửa đường tròn
O
đường kính AB với 2022AB , lấy điểm C (C khác A và
B), từ C kẻ CH vuông góc với AB (H AB). Gọi D là điểm bất kì trên đoạn CH (D khác C
và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E.
1) Chứng minh tứ giác BHDE là tứ giác nội tiếp.
2) Chứng minh AD EC CD AC .
3) Chứng minh
2
2022AD AE BH BA .
4) Khi điểm C di động trên nửa đường tròn (C khác A, B và điểm chính giữa cung
AB), xác định vị trí điểm C sao cho chu vi tam giác COH đạt giá trị lớn nhất.
Câu 5: (1,0 điểm) Cho
1348, 1348a b
. Chứng minh rằng :
2 2
2022a b ab a b
----------------- Hết -----------------
trang
2
SƠ LƯỢC BÀI GIẢI
Câu 1: (1,5 điểm)
1)
2
1
2 1 0
2 5 3 0 2 1 3 0
2
3 0
3
x
x
x x x x
x
x
Vậy tập nghiệm của phương trình là
1
; 3
2
S
2) Hàm số
1 2021y m x
đồng biến trên
1 0 1m m
3)
2 1 2 1 2 2 1 2 1 2 2 2 1 4P a b ab
Câu 2: (2,0 điểm) Cho biểu thức:
1) Rút gọn
P
.
Ta có:
2 9 3 2 1 2 9 3 2 1
2 3
x x x x x x
P
x x x x x x
x x
2 9 3 3 2 1 2
2 9 9 2 3 2
2 3 2 3
x x x x x
x x x x
x x x x
2 1
2 1
3
2 3 2 3
x x
x x x
x
x x x x
2) Ta có
1 1 1 3 4
1 1 1 0 0 0
3 3 3 3
x x x x
P
x x x x
3 0 3 9x x x (TMĐK)
Câu 3: (2,0 điểm)
1) Phương trình đường thẳng
có dạng
y ax b
Vì đường thẳng
song song với đường thẳng 2 1 2, 1y x a b
Vì đường thẳng
đi qua điểm
1; 2 2 1 2 4A b b (TMĐK
1b
)
Vậy phương trình đường thẳng
: 2 4
y x
.
2) Phương trình hoành độ giao điểm của
d
và
P
là:
2 2
2 1 3 2 1 3 0 *x m x m x m x m
d
cắt
P
*
có nghiệm 0
2
2
2
3 7
1 3 0 3 4 0 0
2 4
m m m m m
(đúng với mọi m )
Theo Viét, ta có:
1 2
1 2
2 1
3
x x m
x x m
Khi đó
2
2
2 2 2
1 2 1 2 1 2
2 2 1 2 3 4 10 10M x x x x x x m m m m
2
5 15 15
2
2 4 4
m
. Dấu “=” xảy ra khi
5 5
2 0
2 4
m m
trang
3
Vậy
15
4
Min M
khi
5
4
m
.
Câu 4: (3,5 điểm)
1) Chứng minh tứ giác BHDE là tứ giác nội tiếp.
Xét tứ giác BHDE, ta có:
0
90BHD CH AB
0
90BED (góc nội tiếp chắn nửa đường tròn (O))
Vậy tứ giác BHDE là tứ giác nội tiếp.
2) Chứng minh AD EC CD AC .
Ta có
0
90ACB (góc nội tiếp chắn nửa đường tròn (O))
ACD ABC (cùng phụ
BAC )
mà
AEC ABC (góc nội tiếp cùng chắn cung
AC ), nên
ACD AEC
Xét ACD và AEC , ta có:
CAD (góc chung),
ACD AEC (cmt)
Vậy
ACD
.AEC g g
AD CD
AD EC CD AC
AC EC
(đpcm)
3) Chứng minh
2
2022AD AE BH BA .
Xét AHD và AEB , ta có:
DAH (góc chung),
0
90AHD AEB
(gt và cmt)
Vậy AHD
.
AD AH
AEB g g AD AE AB AH
AB AE
Do đó
2 2
2022
AD AE BH BA AH AB BH BA AB AH HB AB AB AB
4) Xác định vị trí điểm C sao cho chu vi tam giác COH đạt giá trị lớn nhất.
Đặt
,OH a CH b
.
0
: 90COH CHO , nên
2
2 2 2 2 2 2
2022
1011
2
OH CH OC a b
Áp dụng bất đẳng thức
2
2 2
2a b a b
, ta có:
2
2 2 2
2 2 1011 1011 2a b a b a b
Do đó chu vi tam giác COH:
2022
1011 2 1011 1011 2 1
2
OH CH OC a b
Dấu “=” xảy ra khi a b COH vuông cân tại H
0
45AOC sđ
0
45AC
Vậy khi C nằm trên nửa đường tròn sao cho sđ
0
45AC thì chu vi tam giác COH đạt giá trị
lớn nhất là
1011 2 1 (đv chu vi)
Câu 5: (1,0 điểm) Cho 1348, 1348a b . Chứng minh rằng :
2 2
2022a b ab a b
Ta có:
2 2 2 2
3 3
2 3
2 2
a b ab a b ab ab ab ab
Lại có
3 3 3 3
1348, 1348 1348 1348 2022
2 2 2 2
a b ab ab b b a b
Do đó
2 2
2022a b ab a b . Dấu “=” xảy ra khi 1348
1348, 1348
a b
a b
a b
E
H
A
B
O
C
D
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG TỈNH ĐẮK LẮK NĂM HỌC 2021 - 2022 MÔN THI: TOÁN
(Thời gian 120 phút không kể thời gian phát đề)
ĐỀ THI CHÍNH THỨC Ngày thi 09/6/2021
Câu 1: (1,5 điểm) 1) Giải phương trình: 2
2x  5x  3  0 .
2) Cho hàm số y  m  
1 x  2021. Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên  .
3) Cho a  1  2 và b  1  2 . Tính giá trị của biểu thức: P a b  2ab
Câu 2: (2,0 điểm) Cho biểu thức: 2 x  9 x  3 2 x  1 P   
với x  0, x  4, x  9 x  5 x  6 x  2 x  3 1) Rút gọn P .
2) Tìm các giá trị của x để P 1.
Câu 3: (2,0 điểm)
1) Trong mặt phẳng tọa độ Oxy , viết phương trình đường thẳng  đi qua điểm
A1;  2 và song song với đường thẳng y  2x 1.
2) Trong mặt phẳng tọa độ Oxy cho Parabol  P 2
: y x và đường thẳng
d  : y  2m  
1 x m  3. Gọi x , x là hoành độ giao điểm của đường thẳng d  và 1 2
Parabol  P . Tìm giá trị nhỏ nhất của 2 2
M x x . 1 2
Câu 4: (3,5 điểm)
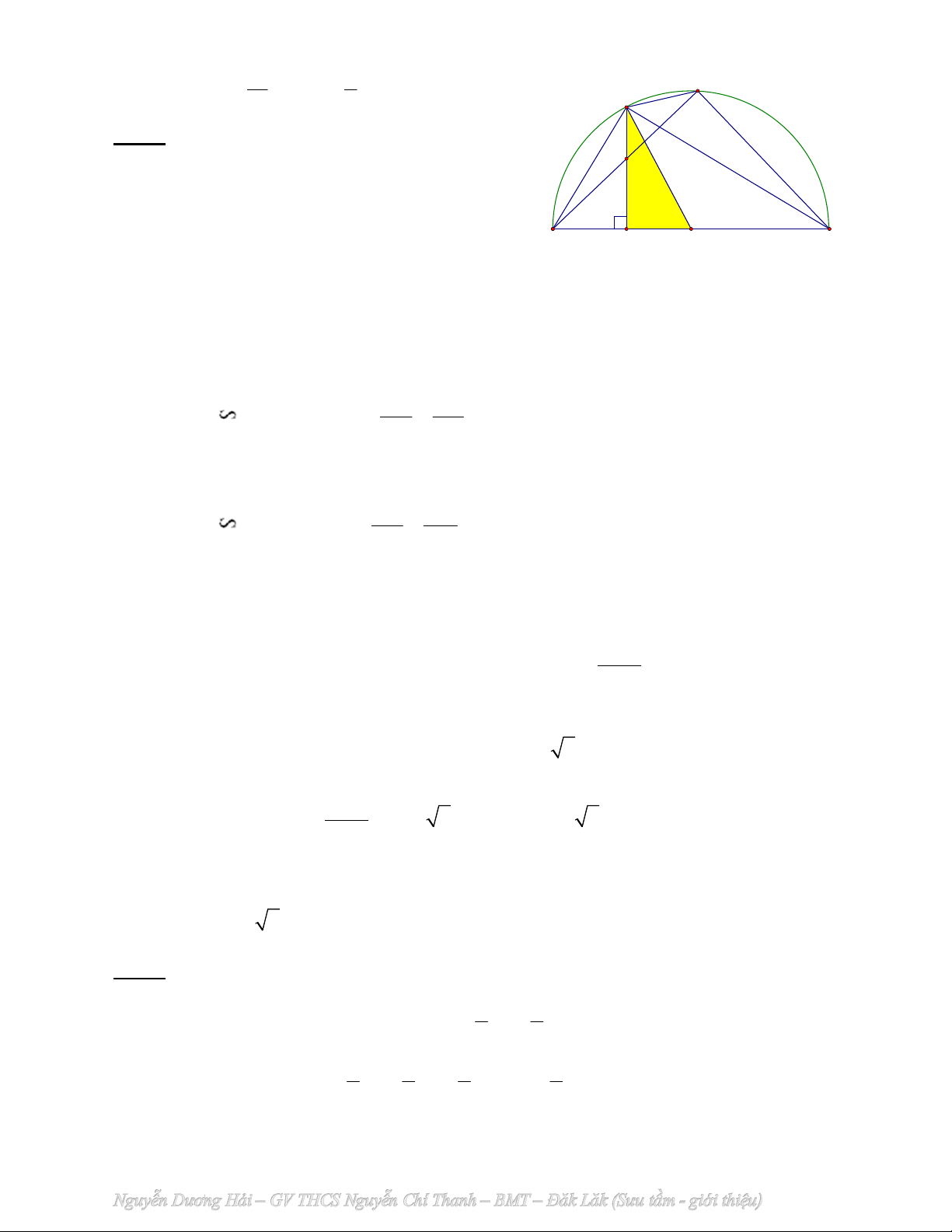
Trên nửa đường tròn O đường kính AB với AB  2022 , lấy điểm C (C khác A và
B), từ C kẻ CH vuông góc với AB (HAB). Gọi D là điểm bất kì trên đoạn CH (D khác C
và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E.
1) Chứng minh tứ giác BHDE là tứ giác nội tiếp.
2) Chứng minh AD EC CD AC . 3) Chứng minh 2
AD AE BH BA  2022 .
4) Khi điểm C di động trên nửa đường tròn (C khác A, B và điểm chính giữa cung
AB), xác định vị trí điểm C sao cho chu vi tam giác COH đạt giá trị lớn nhất.
Câu 5: (1,0 điểm) Cho a  1348, b  1348 . Chứng minh rằng : 2 2
a b ab  2022a b
----------------- Hết ----------------- trang 1
SƠ LƯỢC BÀI GIẢI
Câu 1: (1,5 điểm)  1 2x 1  0 x  1) 2 2x 5x 3 0 2x  1  x 3 0           2  x  3  0   x  3   1 
Vậy tập nghiệm của phương trình là S   ;  3  2 
2) Hàm số y   m  
1 x  2021 đồng biến trên   m 1  0  m  1
3) P a b  2ab  1 2   1 2   21 2 1 2   2  2    1  4
Câu 2: (2,0 điểm) Cho biểu thức: 1) Rút gọn P . 2 x  9 x  3 2 x  1 2 x  9 x  3 2 x 1 Ta có: P       x  5 x  6 x  2 x  3
x  2 x  3 x  2 x  3
2 x  9   x  3 x  3  2 x  
1  x  2 2 x  9  x  9  2x  3 x  2  
x  2 x  3
x  2 x  3
x  2 x x x    1 2 x  1   
x  2 x  3  x  2 x  3 x  3 x  1 x  1 x  1 x  3 4 2) Ta có P  1   1   1  0   0   0 x  3 x  3 x  3 x  3  x  3  0 
x  3  x  9 (TMĐK)
Câu 3: (2,0 điểm)
1) Phương trình đường thẳng  có dạng y ax b
Vì đường thẳng  song song với đường thẳng y  2x 1 a  2, b  1 
Vì đường thẳng  đi qua điểm A1;  2  2 1 b  2   b  4  (TMĐK b  1)
Vậy phương trình đường thẳng  : y  2x  4 .
2) Phương trình hoành độ giao điểm của d  và  P là: 2
x  m   2 2
1 x m  3  x  2m  
1 x m  3  0 *
d  cắt P    * có nghiệm     0 2  3  7
  m   2 1   m  3 2
 0  m  3m  4  0  m    0    
(đúng với mọi m )  2  4
x x  2 m 1 1 2   Theo Viét, ta có:  x x m  3  1 2 2 2 Khi đó 2 2
M x x   x x   2x x  2m  
1   2m  3 2
 4m  10m  10  1 2 1 2 1 2   2  5  15 15 5 5  2m     
. Dấu “=” xảy ra khi 2m   0  m   2  4 4 2 4 trang 2 15 5
Vậy MinM   khi m  . E C 4 4
Câu 4: (3,5 điểm)
1) Chứng minh tứ giác BHDE là tứ giác nội tiếp. D
Xét tứ giác BHDE, ta có:  0
BHD  90 CH AB  0 A B
BED  90 (góc nội tiếp chắn nửa đường tròn (O)) H O
Vậy tứ giác BHDE là tứ giác nội tiếp.
2) Chứng minh AD EC CD AC . Ta có  0
ACB  90 (góc nội tiếp chắn nửa đường tròn (O))  
ACD ABC (cùng phụ  BAC ) mà  
AEC ABC (góc nội tiếp cùng chắn cung  AC ), nên   ACD AEC Xét ACD và AEC , ta có:  CAD (góc chung),  
ACD AEC (cmt) AD CD Vậy ACD
AEC g.g   
AD EC CD AC (đpcm) AC EC 3) Chứng minh 2
AD AE BH BA  2022 .
Xét AHD và AEB , ta có: DAH (góc chung),   0
AHD AEB  90 (gt và cmt) AD AH Vậy AHD
AEB g.g   
AD AE AB AH AB AE
Do đó AD AE BH BA AH AB BH BA AB   AH HB  2 2
AB AB AB  2022
4) Xác định vị trí điểm C sao cho chu vi tam giác COH đạt giá trị lớn nhất.
Đặt OH a, CH b . 2   2022 0  C
OH : CHO  90 , nên 2 2 2 2 2 2
OH CH OC a b   1011    2  2
Áp dụng bất đẳng thức a b   2 2
2 a b  , ta có:
a b2   2 2 a b  2 2
 2 1011  a b  1011 2
Do đó chu vi tam giác COH: 2022
OH CH OC a b
 1011 2  1011  101  1 2   1 2
Dấu “=” xảy ra khi a b C
OH vuông cân tại H  0
AOC  45  sđ  0 AC  45
Vậy khi C nằm trên nửa đường tròn sao cho sđ  0
AC  45 thì chu vi tam giác COH đạt giá trị lớn nhất là 101  1 2   1 (đv chu vi)
Câu 5: (1,0 điểm) Cho a  1348, b  1348 . Chứng minh rằng : 2 2
a b ab  2022a b 3 3 Ta có: 2 2 2 2
a b  2ab a b ab  3ab ab ab 2 2 3 3 3 3
Lại có a  1348, b  1348  ab ab  1348b
1348b  2022a b 2 2 2 2 a b Do đó 2 2
a b ab  2022a b . Dấu “=” xảy ra khi
a b  1348 
a  1348, b  1348  trang 3