

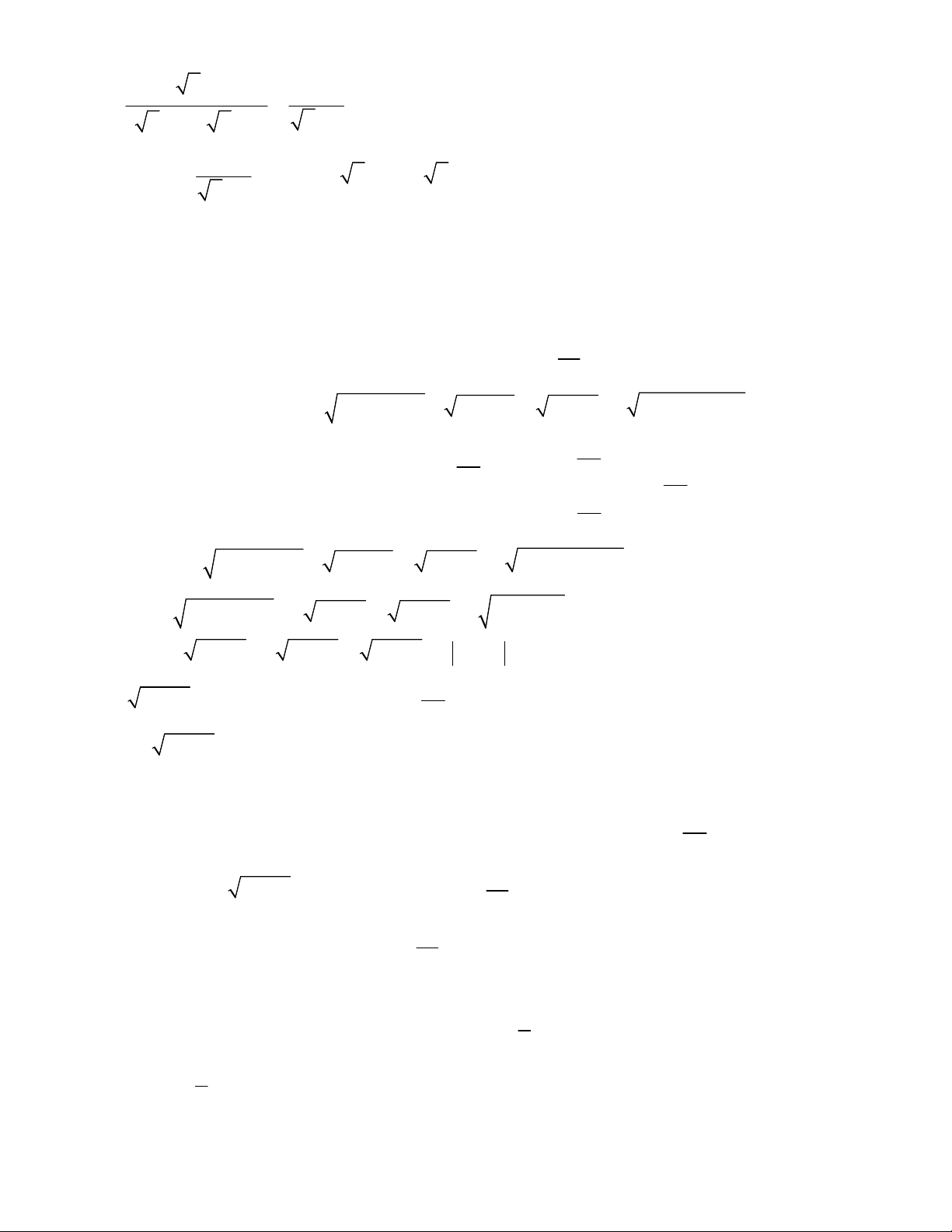

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT, THPT CHUYÊN TỈNH HẬU GIANG NĂM HỌC 2021-2022 MÔN THI: TOÁN – THPT ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề
(Đề thi gồm có 02 trang)
I. Phần trắc nghiệm: (2,0 điểm)
Câu 1. Cho hàm số f x 3x 1 . Giá trị của f 1 bằng A. -2. B. 2. C. 1. D. 0.
Câu 2. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d có phương trình y 2 7x . Hệ số
góc của đường thẳng d bằng 7 B. 7. C. -7. D. 2. A. . 2 Câu 3. Phương trình 2
x 7x 10 0 có một nghiệm bằng A. 5 . B. -7. C. -2. D. 5. 3 x y 7
Câu 4. Hệ phương trình có nghiệm duy nhất là 5 x y 9 x 2 x 2 x 2 x 2 A. . B. . C. . D. . y 1 y 1 y 3 y 3
Câu 5. Điều kiện của x để biểu thức x 2 có nghĩa là A. x 2 . B. x 2 . C. x 2 . D. x 2 .
Câu 6. Giá trị của biểu thức 3 2 2 bằng A. 1 2 2 . B. 2 2 . C. 2 1. D. 1 2 .
Câu 7. Cho tam giác ABC vuông tại A có AB 6c ,
m BC 10cm và đường cao AH với H BC .
Khi đó độ dài đoạn BH bằng 18 24 3 A. cm . B. cm . C. 2cm. D. cm . 5 5 5
Câu 8. Cho tứ giác ABCD nội tiếp trong đường tròn (O). Biết 0 BAD 105 và 0 DBC 45 . Khi đó, giá trị của cos BDC bằng 6 2 2 1 3 A. . B. . C. . D. . 4 2 2 2
II. Phần tự luận: (8,0 điểm) Câu 1 (2,0 điểm)
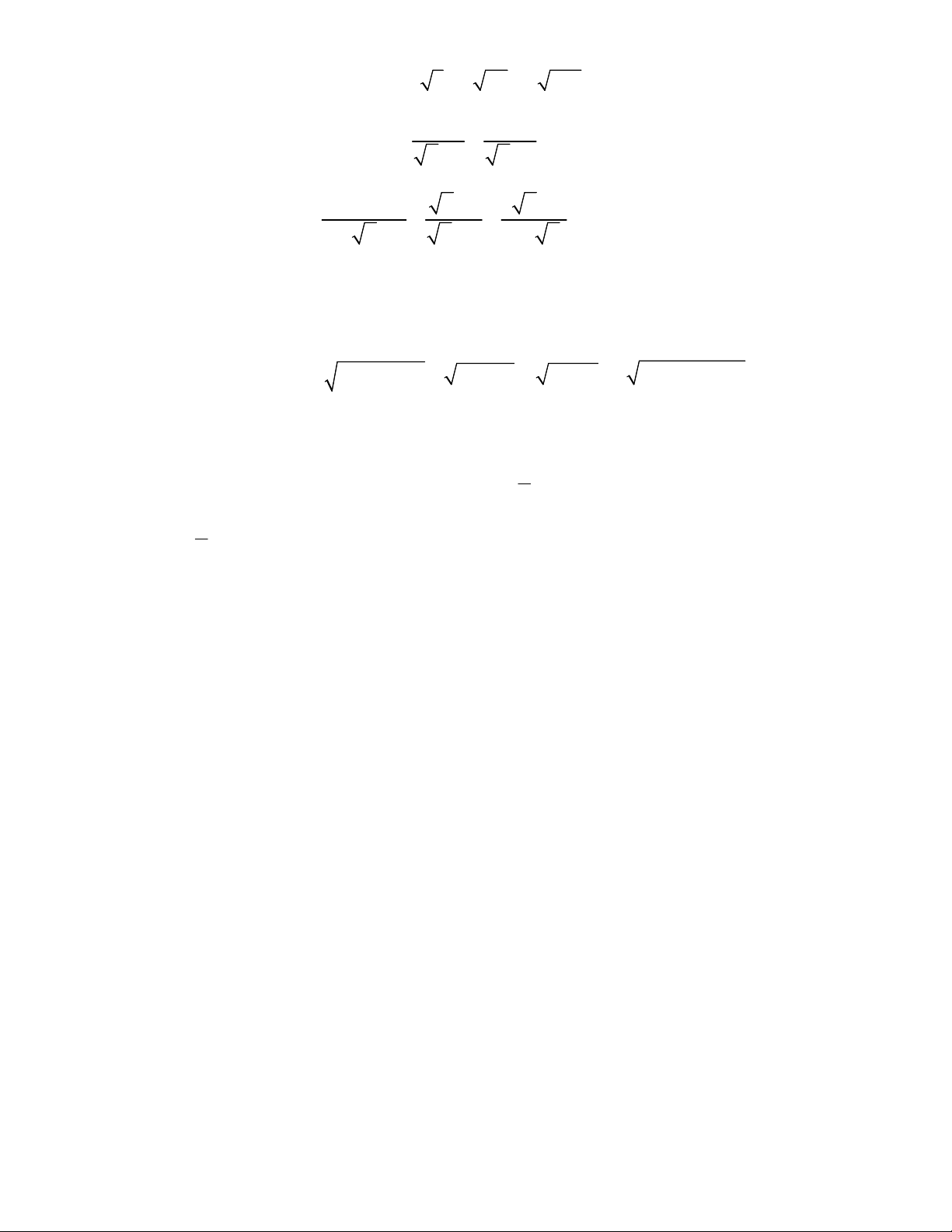
a) Tính giá trị của biểu thức A 3 3 7 27 2 243 . x 2 x
b) Tính giá trị của biểu thức B khi x 4. x 1 x 1 2 x 13 x 1 3 x 2 c) Cho biểu thức C
với x 0, x 9 . Tìm x để C 1. x x 6 x 2 3 x Câu 2 (2,0 điểm) a) Giải phương trình 2 3x 5x 2 0 . b) Giải phương trình: x 2 49 3
2 12x 8 3x 2 3 9x 12x 4 7 . Câu 3 (1,5 điểm) 1
Trong mặt phẳng tọa độ Oxy, cho hàm số 2
y x có đồ thị (P) và đường thẳng d có phương 2 1 trình 2
y x m m 1, với m là tham số. 2 a) Vẽ đồ thị (P).
b) Tìm m để đường thẳng d cắt (P) tại 2 điểm phân biệt có hoành độ x , x sao cho 1 2 3 3 x x 68 . 1 2 Câu 4 (2,0 điểm)
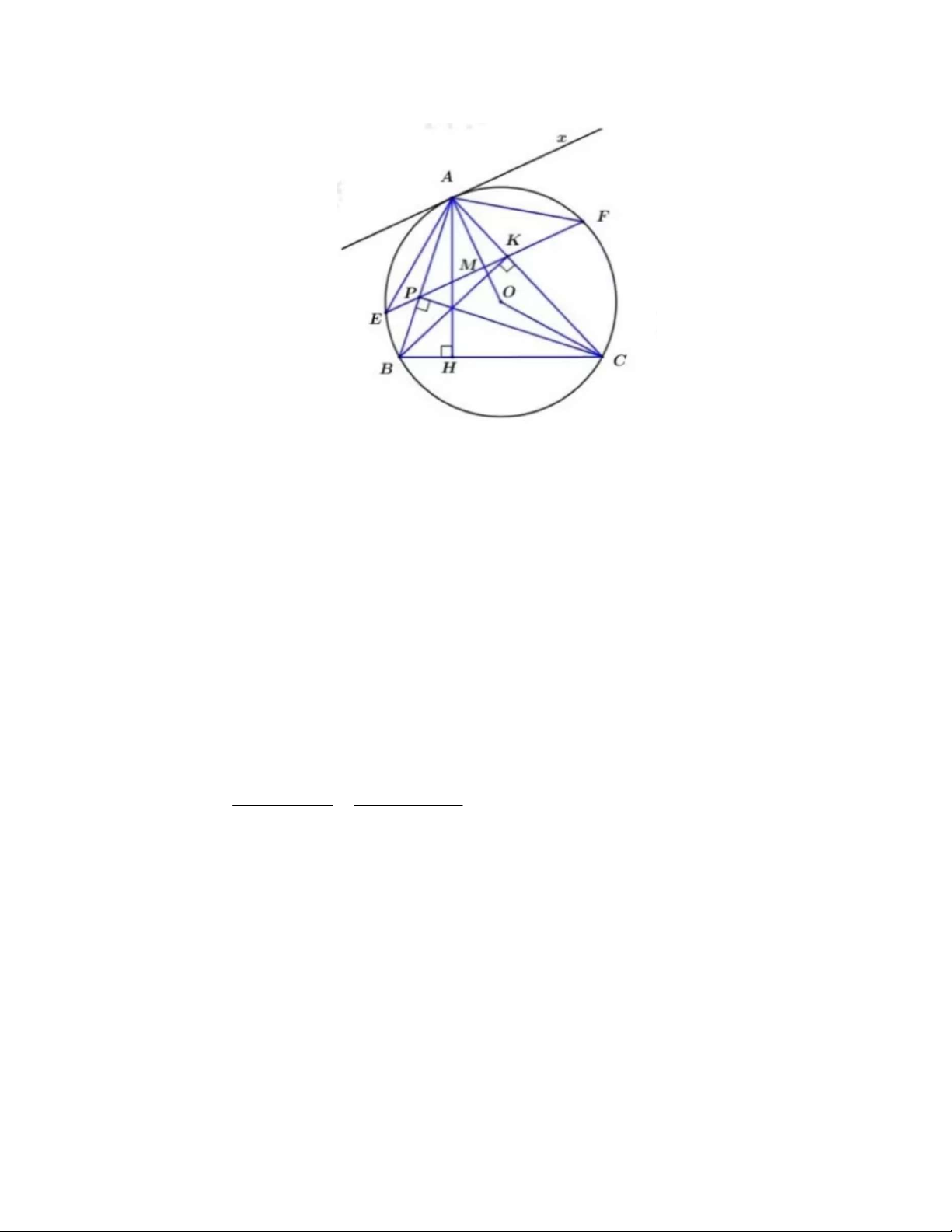
Cho tam giác nhọn ABC nội tiếp trong đường tròn (O). Vẽ các đường cao AH, BK và CP của
tam giác ABC, với H BC, K AC, P A . B
a) Chứng minh tứ giác BPKC nội tiếp. b) Chứng minh rằng BAH OAC.
c) Đường thẳng PK cắt (O) tại hai điểm E và F. Chứng minh OA là tia phân giác của EAF . Câu 5 (0,5 điểm) 3 2
y 12x y 8 3x 2 1 6xy
Giải hệ phương trình (với x, y ). 2
xy 2y x x 10 0
------------------HẾT-------------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HDC KỲ THI TUYỂN SINH LỚP 10 THPT, THPT CHUYÊN TỈNH HẬU GIANG NĂM HỌC 2021-2022 MÔN THI: TOÁN – THPT (HDC gồm có 03 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề
I. Phần trắc nghiệm (2,0 điểm) 1. B 2.C 3.D 4.A 5.C 6.D 7.A 8.C
II. Phần tự luận (8,0 điểm) Câu 1 (2,0 điểm)
a) Tính giá trị của biểu thức A 3 3 7 27 2 243 .
Ta có: A 3 3 7 27 2 243 A 3 3 21 3 18 3 A 3 2118 3 A 0 Vậy A = 0. x 2 x
b) Tính giá trị của biểu thức B khi x 4. x 1 x 1 x 0 x 0 ĐKXĐ: x 1 0 x 1
Thay x = 4 (TM ĐKXĐ vào biểu thức B ta có: 4 2 4 2 4 B 4 1 4 1 2 1 2 1 4 10 2 3 3 2 x 13 x 1 3 x 2 c) Cho biểu thức C
với x 0, x 9 . Tìm x để C 1. x x 6 x 2 3 x 2 x 13 x 1 3 x 2 C x x 6 x 2 3 x 2x 13 x 1 3 x 2 C x 23 x x 2 3 x 2 x 13 x
1 3 x 3 x 2 x 2 C x 2 x 3 2
x 13 x 2 x 3 3x 4 x 4 C x 2 x 3 6 x 2 6 C x 2 x 3 x 3 6 Để C = 1 thì
1 6 x 3 x 9 x 81(TM ) x 3
Vậy với x = 81 thì C = 1. Câu 2 (2,0 điểm) a) Giải phương trình 2 3x 5x 2 0 . Ta có 2
5 4.32 49 0 nên phương trình đã cho có 2 nghiệm phân biệt 1 x 2; x 1 2 3 b) Giải phương trình: x 2 49 3
2 12x 8 3x 2 3 9x 12x 4 7 2 3x 2 0 2 x x 3 2 12x 8 0 3 x ĐKXĐ: 9 x 12x 4 0 3x 22 2 3 2 0 x 3 x 2 49 3
2 12x 8 3x 2 3 9x 12x 4 7 Ta có: x x x x 2 49 3 2 2 3 2 3 2 3 3 2 7
7 3x 2 2 3x 2 3x 2 3 3x 2 7 2
4 3x 2 33x 2 7 0 x (Do 3 nên 3x + 2 >0) t 3x 2(t 0) 2 3t 4t 7 0(*) Đặt
, phương trình trở thành t 1(TM )
Ta có a + b + c = 3 + 4 + (-7) = 0 nên pt (*) có hai nghiệm phân biệt 7 t (KTM ) 3 1
3x 2 1 3x 2 1 x Với t = 1, suy ra 3 1 x
Vậy phương trình có nghiệm 3 . Câu 3 (1,5 điểm) 1
Trong mặt phẳng tọa độ Oxy, cho hàm số 2
y x có đồ thị (P) và đường thẳng d có phương 2 1 trình 2
y x m m 1, với m là tham số. 2 a) Vẽ đồ thị (P). 1
Parabol (P) có hệ số a
0 nên đồng biến với x > 0 và nghịch biến với x < 0. Đồ thị hàm 2
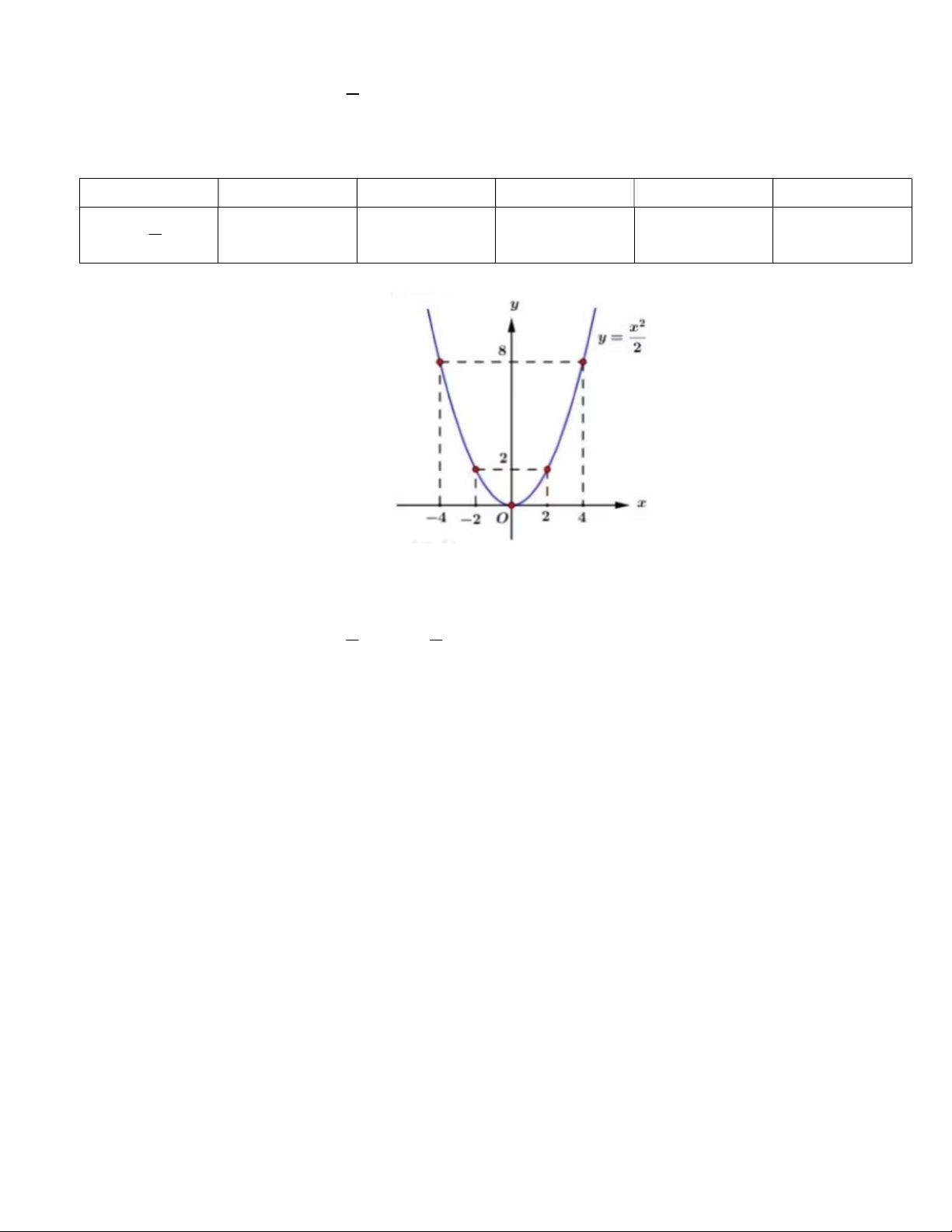
số đi qua gốc tọa độ O(0;0) và nhận Oy làm trục đối xứng. Bảng giá trị x -4 -2 0 2 4 1 2 y x 8 2 0 2 8 2 Vẽ đths:
b) Tìm m để đường thẳng d cắt (P) tại 2 điểm phân biệt có hoành độ x , x sao cho 1 2 3 3 x x 68 . 1 2 1 1 PT hoành độ giao điểm: 2 2 2 2
x x m m 1 x 2x m 2m 2 0(*) 2 2
Để đường thẳng d cắt (P) tại 2 điểm phân biệt thì pt (*) có hai nghiệm phân biệt
m m m 2 2 ' 0 2 3 0 1 2 0 Do m 2 1 0m nên m 2
1 2 0m , do đó pt (*) luôn có hai nghiệm phân biệt với
mọi m đường thẳng d luôn cắt (P) tại 2 điểm phân biệt có hoành độ x , x 1 2 x x 2 1 2
Khi đó áp dụng ĐL Viet ta có: 2 x x m 2m 2 1 2 3 3
Theo bài ra ta có: x x 68 1 2
x x 3 3x x x x 68 1 2 1 2 1 2 3 2 3 2 m 2m 2.2 68 2 6m 12m 48 0 2 m 6m 8 0(**)
PT (**) có hai nghiệm phân biệt m 2;m 4 . 1 2 Câu 4 (2,0 điểm)
Cho tam giác nhọn ABC nội tiếp trong đường tròn (O). Vẽ các đường cao AH, BK và CP của
tam giác ABC, với H BC, K AC, P A . B
a) Chứng minh tứ giác BPKC nội tiếp. Xét tứ giác BPKC có: BPC 0
BKC 90 nên P, K cùng thuộc đường tròn đường kính BC.
Vậy tứ giác BPKC nội tiếp đường tròn đường kính BC. b) Chứng minh rằng BAH OAC.
ABH vuông tại H nên BAH 0 AHB BAH 0 ABC 0 90 90 BAH 90 ABC (1) OAC O AC có OA = OC nên O AC cân tại O OCA OAC OCA Ta có: 0 AOC 180 AOC 2 180 0 OAC 180 AOC 0 OAC 2 AOC 2 Lại có:
ABC (góc nội tiếp và góc ở tâm cùng chắn cung AC). 0 180 0 AOC 180 2 ABC 0 OAC 90 ABC 2 2 (2) Từ (1) và (2) ta suy ra BAH OAC
c) Đường thẳng PK cắt (O) tại hai điểm E và F. Chứng minh OA là tia phân giác của EAF .
Kẻ tiếp tuyến Ax với (O). xAC Ta có
ABC (góc nội tiếp và góc ở tâm cùng chắn cung AC). AKP Mà
ABC (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp BPKC) xAC AK .
P Hai góc này lại ở vị trí so le trong. Ax / /PK.
Ta có: Ax OA (do Ax là tiếp tuyến của (O) tại A) PK OA
Gọi M OA PK , ta có EF OA tại M. Suy ra M là trung điểm của EF.
Suy ra tam giác AEF có OA là đường cao đồng thời là trung tuyến
Suy ra tam giác AEF cân tại A.
Vậy đường cao AO là phân giác của góc EAF. Câu 5 (0,5 điểm) 3 2
y 12x y 8 3x 2 1 6xy
Giải hệ phương trình (với x, y ). 2
xy 2y x x 10 0 3 2
y 12x y 8 3x 2 1 6xy (1) 2
xy 2y x x 10 0 (2) Ta có: 3 2 y 12x y 8 3 x 2 1 6xy 3 2 2 3
8x 12x y 6xy y 8 2x3 32x2 2 3 .y 3.2 . x y y 8 3 2x y 8 2x y 2 y 2x 2
Thay vào phương trình (2) ta có
x 2x 2 22x 2 2 x x 10 0 2 2
2x 2x 4x 4 x x 10 0 2 x 5x 14 0(*) 3 1 0 Do đó pt(*) vô nghiệm.
Vậy hpt đã cho vô nghiệm.




