

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT TỈNH QUẢNG NINH NĂM 2022-2023
Môn thi: TOÁN (Dành cho mọi thí sinh) ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 120 phút, không kể thời gian giao đề (Đề thi này có 01 trang) Câu 1. (2,75 điểm)
a) Thực hiện phép tính 2 9 4 . 1 1 2
b) Rút gọn biểu thức A : với x 0 và x 1. x 1 x 1 x 1
c) Tìm các giá trị của m để đường thẳng d : y 2x 3m đi qua điểm B(1;5). 2 x y 7
d) Giải hệ phương trình . x y 2 Câu 2. (1,75 điểm) Cho phương trình 2 x 2m
1 x 2m 1 0 ( m là tham số)
a. Giải phương trình với m 2
b. Tìm các giá trị của m để phương trình có hai nghiệm x ; x thỏa mãn 2x 3x 3x x 1 1 1 2 1 2 1 2
Câu 3. (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Hai đội công nhân cùng làm một công việc thì hoàn thành trong 12 ngày. Nếu họ làm riêng
thì đội II hoàn thành công việc hết nhiều thời gian hơn đội I là 10 ngày. Hỏi nếu làm riêng, mỗi
đội phải làm trong bao nhiêu ngày để xong công việc. Câu 4. (3,5 điểm)
Cho đường tròn tâm 0, đường kính AB, dây CD vuông góc với AB tại F. Gọi M là một điểm
thuộc cung nhỏ BC( M khác B, M khác C), hai đường thẳng AM và CD cắt nhau tại E.
a) Chứng minh tứ giác BMEF nội tiếp;
b)Chứng minh tia MA là phân giác của góc CMD b) Chứng minh 2 AC AE.AM ;
c) Gọi I là giao điểm của hai đường thẳng MD và AB, N là giao điểm của hai đường thẳng
AM và BC. Chứng minh tâm đường tròn ngoại tiếp tam giác CEN nằm trên đường thẳng CI. Câu 5. (0,5 điểm)
Một tỉnh dự định làm đường điện từ điểm A
trên bờ biển đến điểm B trên một hòn đảo. B
cách bờ một khoảng BB’=2km, A cách B’ một
khoảng AB’ = 3 km (hình vẽ). Biết chi phí làm
1km đường điện trên bờ là 5 tỷ đồng, dưới
nước là 13 tỷ đồng. Tìm vị trí điểm C trên đoạn
bờ biển AB’ sao cho khi làm đường điện theo
đường gấp khúc ACB thì chi phí thấp nhất(coi
bờ biển là đường thẳng).
............................ Hết ...........................
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ........................................................Số báo danh: ......................
Chữ kí của cán bộ coi thi 1: .....................Chữ kí của cán bộ coi thi 2:....................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM THI TUYỂN SINH TỈNH QUẢNG NINH
VÀO LỚP 10 THPT NĂM HỌC 2022-2023
Môn thi : TOÁN (Dành cho mọi thí sinh) ĐỀ THI CHÍNH THỨC
(Hướng dẫn này có 02 trang) Câu Sơ lược lời giải Điểm
a. 2 9 4 2.3 2 6 2 4 0,5 đ b. với x 0 và x 1. 1 1 2 x 1 x 1 x 1 A : . x 1 x 1 x 1 x 1 x 1 2 1,0 đ Câu 1 2 x x 1 2,75 . x điểm x 1 2
c. Đường thẳng d : y 2x 3m đi qua điểm B(1;5) 5 2.1 3m 0,5 đ 3m 3 m 1 0,25 đ 2 x y 7 3x 9 x 3 d.
Vậy hệ phương trình có nghiệm (3;-1) 0,5đ x y 2 x y 2 y 1
a) Với m = 2, phương trình trở thành 2 x 2x 5 0 0,25 đ
' 6 0 phương trình có hai nghiệm phân biệt x 1 6, x 1 6 0,5 đ 1 2 b) m 2 2 2 '
1 2m 1 m 2m 1 2m 1 m 2 0với mọi m 0,25 đ
=> Phương trình luôn có hai nghiệm phân biệt x1 , x2 với mọi m Câu 2 Theo định lý Vi – ét: 1,75 x x 2m 2 1 2 điểm 0,25 đ x .x 2 m 1 1 2
2x 3x 3x x 11 3 x x 3x x x 11 1 2 1 2 1 2 1 2 1 0,25đ 3(2m 2) 3( 2 m1) x 1 1 x 2 1 1 7
x1 là nghiệm của phương trình nên: 2
2 4(m1) 2 m1 0 m 0,25đ 6
Gọi thời gian đội I làm riêng để hoàn thành công việc là x(ngày)(đk: x > 0) 0,25 đ
Thời gian đội II làm riêng để hoàn thành công việc là x + 10 (ngày) 1 1 0,25 đ
Trong 1 ngày đội I làm được (công việc), đội II làm được (công việc) x x 10 Câu 3
Vì hai đội cùng làm thì hoàn thành công việc trong 12 ngày nên ta có phương trình: 1,5 điểm 1 1 1 2 x 14x 120 0 0,25 đ x x 10 12 Giải pt được x 6
( không thỏa mãn đk); x 20 ( thỏa mãn đk). 1 2 0,5 đ
Kết hợp với điều kiện x = 20. Vậy nếu làm riêng thì đội I hoàn thành công việc trong
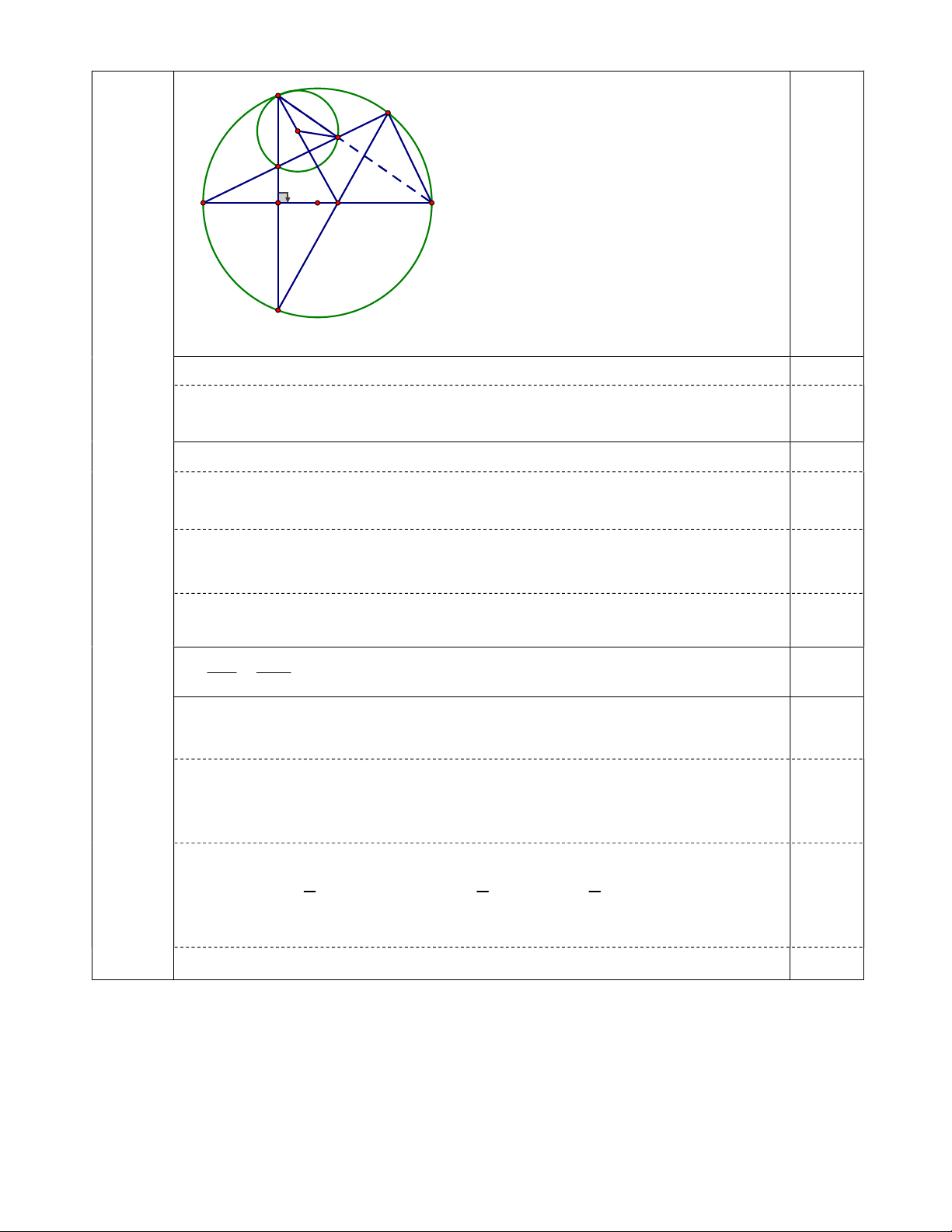
20 ngày, đội II trong 30 ngày 0,25 đ 1 C M K N E A B F O I 0,25 đ D Hình vẽ (đủ cho ý a)
a) M thuộc đường tròn đường kính AB=> 0 AMB 90 hay 0 EMB 90 0,25 đ Do 0
EFB 90 ( Dây CD vuông góc với đường kính AB) 0,25 đ Tứ giác BMEF có EMB 0 EFB 180 0,25đ
nên Tứ giác BMEF nội tiếp
b) Đường kính AB vuông góc với dây CD => AC = AD 0,25 đ
CMA nội tiếp (O) chắn cung AC,
DMA nội tiếp (O) chắn cung AD nên Câu 4 0,5 đ CMA 3,5
DMA => MA là phân giác của CMD điểm ACD c)
AMD ( Cùng chắn cung AD), mà CMA DMA ( chứng minh a) => 0,5 đ ACE AMC
Xét tam giác ACE và tam giác AMC có A chung , ACE AMC 0,25 đ
=> tam giác ACE đồng dạng tam giác AMC (g-g) AC AM 2 AC A . D AM (đpcm) 0,25 đ AE AC d) Ta có AMC ABC (cùng chắn AC ) mà AMC AMD NMI => NBI 0,25 đ
=> Tứ giác NMBI nội tiếp => 0 NIB 0 180 NMB 90
Điểm C thuộc đường tròn đường kính AB => 0 ACB 90 Tứ giác ACNI có ACN 0
AIN 180 nên Tứ giác ACNI nội tiếp đường tròn => 0,25 đ NAI NCI (1)
Gọi K là tâm đường tròn ngoại tiếp C EN . Ta có K CN cân tại K KCN 1 0 KNC CKN 0 1 0 1 180 - 90 - CKN 90 - sd 0 CN 90 CEN 2 2 2 0,25 đ Do A EF vuông => 0 EAF 0 90 AEF 90 CEN KCN NAI (2) Từ (1), (2) => KCN
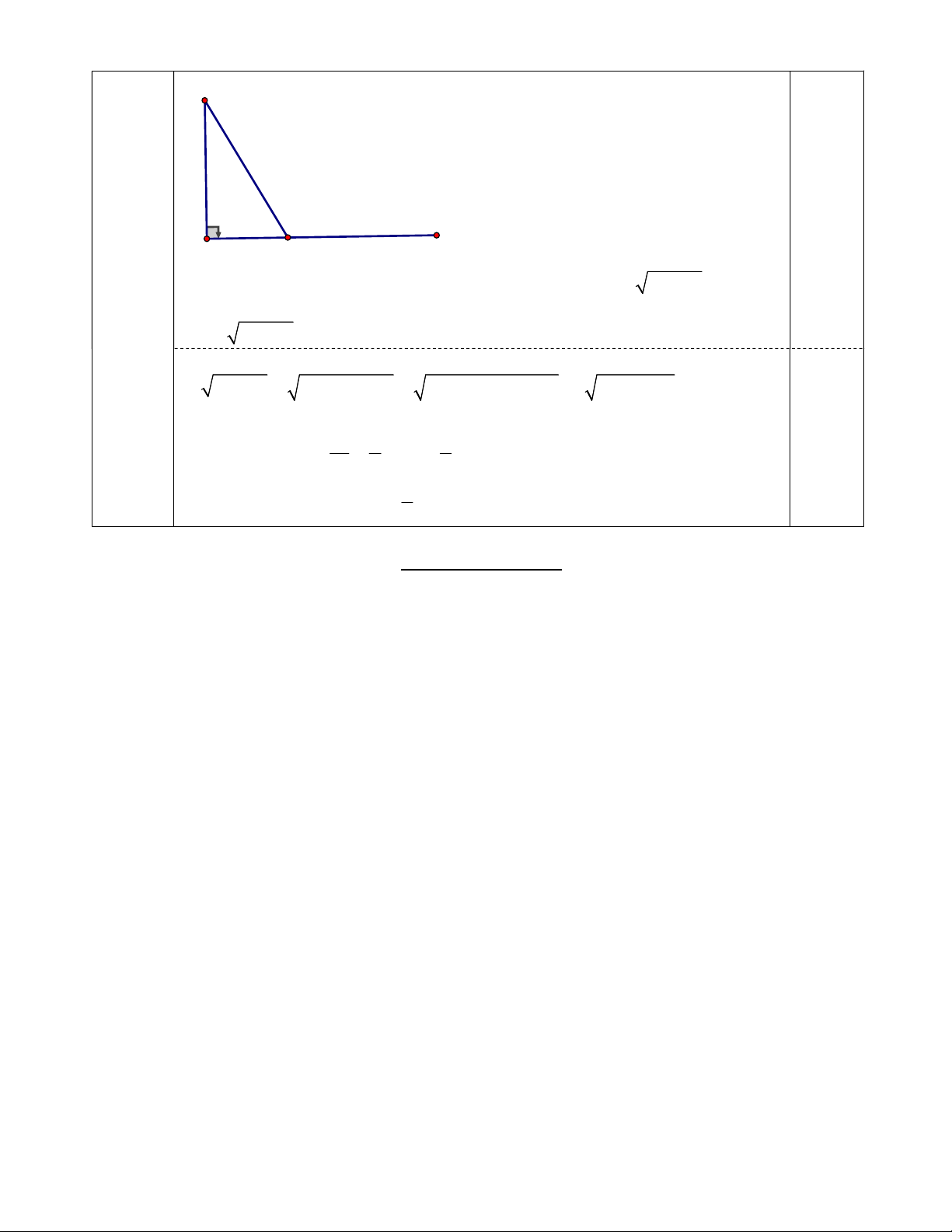
ICN nên ba điểm C, K, I thẳng hàng 0,25 đ 2 Câu 5 B 0,5 điểm 0,25 đ A B' x C
Đặt B’C = x (km)(đk : 0 x 3) =>AC = 3 - x(km), BC = 2 2 2 x (km)
Tổng số tiền làm đường điện theo đường gấp khúc ACB là : T =13 2 2
2 x +5(3 - x) (tỷ đồng) Ta có 2 2 2 2 2 2 2 2 2
13 2 x 169(2 x ) (12 5 )(2 x ) (24 5x) 24 5x
T 24 5x 15 5x 39 12 5 5 0,25 đ Dấu đẳng thức khi x . 2 x 6 5
Vậy C cách B’ một khoảng km thì chi phí thấp nhất 6 Các chú ý khi chấm
1. Hướng dẫn chấm này chỉ trình bày sơ lược một cách giải. Bài làm của học sinh phải
chi tiết, lập luận chặt chẽ, tính toán chính xác mới cho điểm tối đa.
2. Với các cách giải đúng nhưng khác đáp án, tổ chấm trao đổi và thống nhất điểm chi
tiết nhưng không được vượt quá số điểm dành cho câu hoặc phần đó. Mọi vấn đề phát sinh
trong quá trình chấm phải được trao đổi trong tổ chấm và chỉ cho điểm theo sự thống nhất của cả tổ.
3. Điểm toàn bài là tổng số điểm các phần đã chấm, không làm tròn điểm.
............................. Hết .......................... 3




