Đề tuyển sinh vào lớp 10 môn Toán năm 2022 – 2023 sở GD&ĐT Trà Vinh
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi chính thức kỳ thi tuyển sinh vào lớp 10 môn Toán năm học 2022 – 2023 sở Giáo dục và Đào tạo tỉnh Trà Vinh; đề thi gồm hai phần: phần chung dành cho tất cả các thí sinh (07 điểm) và phần tự chọn (03 điểm), thời gian học sinh làm bài thi là 120 phút (không kể thời gian giao đề). Mời các bạn đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT TRÀ VINH
NĂM HỌC 2022 – 2023 ĐỀ CHÍNH THỨC Môn thi: TOÁN
Thời gian: 120 phút (không kể thời gian phát đề) HƯỚNG DẪN GIẢI I.
PHẦN CHUNG DÀNH CHO TẤT CẢ CÁC THÍ SINH Câu 1. (2,0 điểm)
a) Tính giá trị biểu thức sau: A = 12 − 2 27 + 3 75 . Lời giải A = 12 − 2 27 + 3 75 = − + A 2 3 2.3 3 3.5 3 A = 2 3 − 6 3 +15 3 A =11 3 Vậy A =11 3 . 3 x + y =11
b) Giải hệ phương trình: 2x − y = 4 Lời giải 3 x + y =11 5x =15 x = 3 ⇔ ⇔ 2x y 4 2x y 4 − = − = y = 2
Vậy hệ phương trình có nghiệm (3;2).
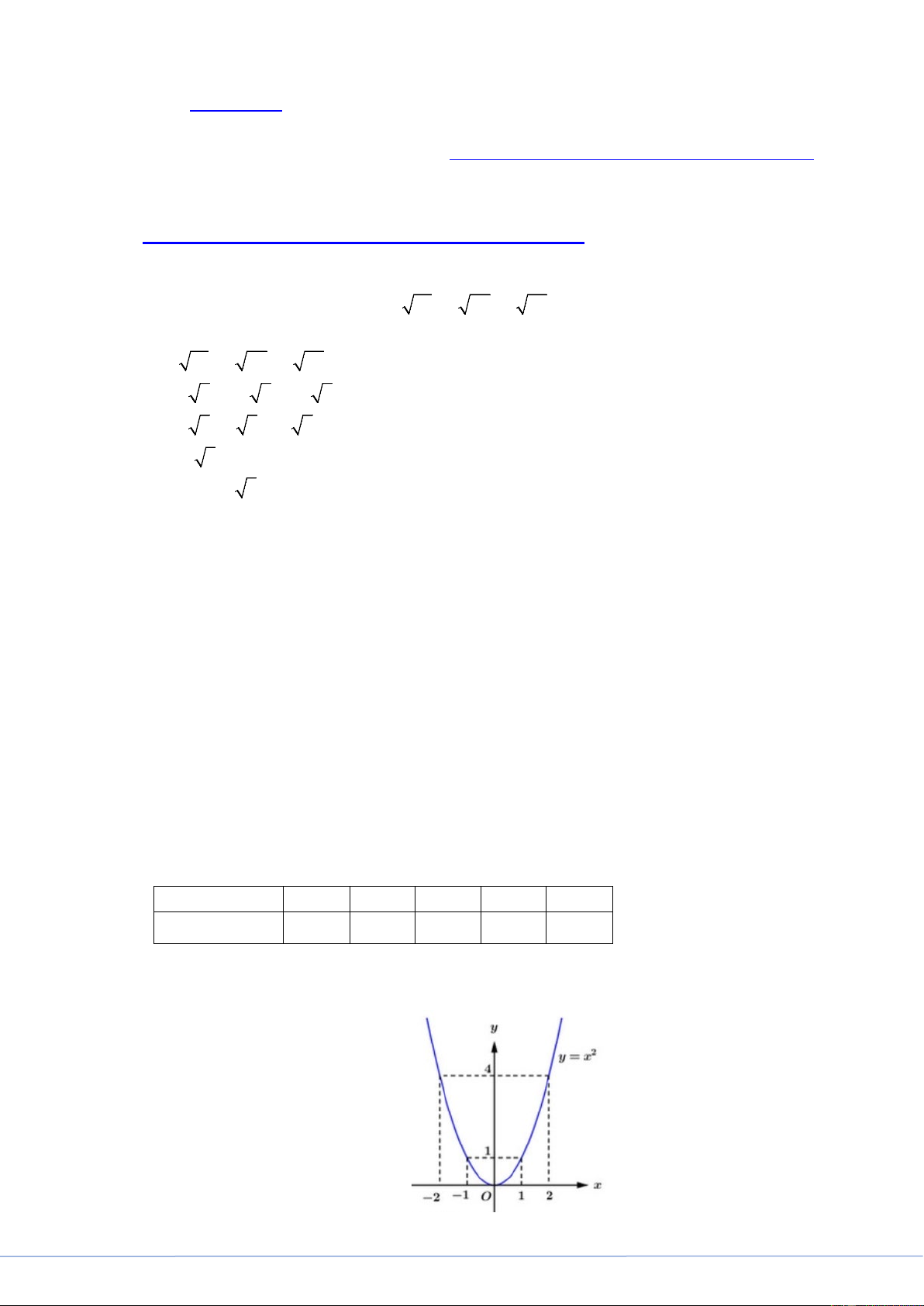
Câu 2. (2.0 điểm) Cho parabol 2
(P) : y = x .
a) Lập bảng giá trị và vẽ Parabol (P) .
b) Tìm tọa độ giao điểm của (P) và đường thẳng (d) : y = 4x − 3 bằng phép tính. Lời giải
a) Lập bảng giá trị và vẽ parabol 2
(P) : y = x . Bảng giá trị: 2
(P) : y = x x 2 − 1 − 0 1 2 2 y = x 4 1 0 1 4 Suy ra parabol 2
(P) : y = x là đường cong đi qua các điểm ( 2; − 4),( 1 − ; ) 1 ,(0;0),(1; ) 1 ,(2;4) Vẽ đồ thị 2
(P) : y = x Trang 2
b) Phương trình hoành độ giao điểm của 2
(P) : y = x và (d) : y = 4x − 3 x = 1 2 2
x = 4x − 3 ⇔ x − 4x + 3 = 0 ⇔ x = 3 Với 2
x =1⇒ y =1 =1⇒ A(1; ) 1 Với 2
x = 3 ⇒ y = 3 = 9 ⇒ B(3;9)
Vậy giao điểm của (P) và (d) là A(1; ) 1 , B(3;9) .
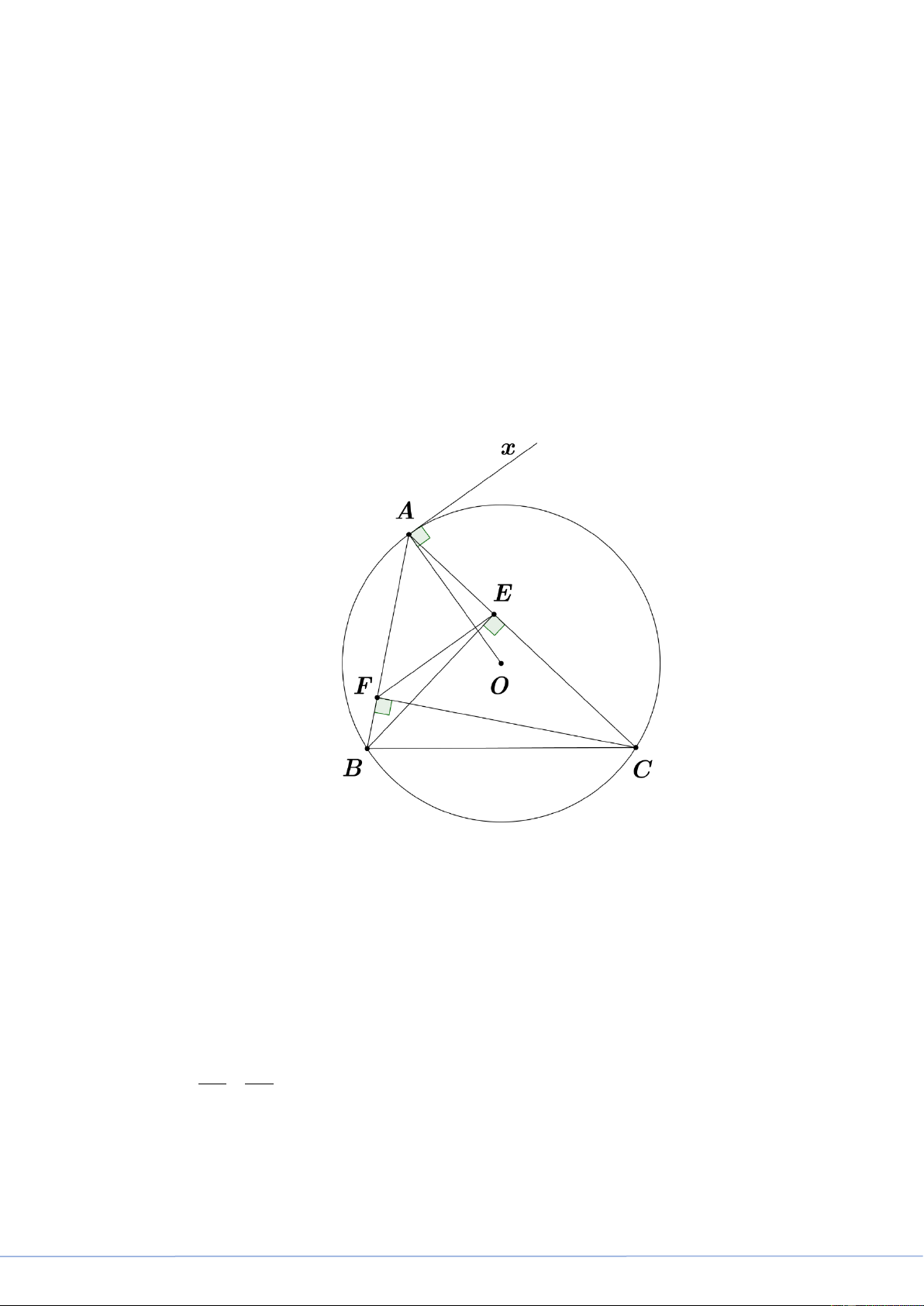
Câu 3. (3,0 điểm) Cho tam giác nhọn ABC nội tiếp đường tròn (O) . Hai đường cao BE,CF cắt nhau
tại H (E ∈ AC, F ∈ AB). Chứng minh rằng:
a) Tứ giác BCEF nội tiếp đường tròn;
b) AE.BC = EF.AB ; c) OA ⊥ EF. Lời giải
a) Xét tứ giác BCEF có =
BFC BEC = 90° (vì BE,CF là hai đường cao của tam giác ABC ). Mà
BFC; BEC cùng nhìn cạnh BC .
Suy ra tứ giác BCEF nội tiếp đường tròn (tứ giác có hai đỉnh kề cùng nhìn 1 cạnh dưới 1 góc bằng nhau). b) Xét A ∆ EF và A ∆ BC có BAC chung và =
AFE ACB (tứ giác BCEF nội tiếp). Suy ra A ∆ EF ∽ A ∆ BC (g – g) Suy ra AE EF =
⇒ AE.BC = A . B EF. AB BC
c) Kẻ tia Ax là tiếp tuyến của đường tròn (O) . Ta có: =
CAx ABC (góc nội tiếp bằng góc giữa tiếp tuyến và dây cung cùng chắn cung AC ). Mà: =
ABC AEF (tứ giác BCEF nội tiếp). Suy ra : =
CAx AEF . Mặt khác CA ;
x AEF nằm ở vị trí so le trong. Trang 3
Suy ra Ax//EF . Mà Ax ⊥ OA ⇒ OA ⊥ EF (đpcm).
III. PHẦN TỰ CHỌN
Thí sinh chọn một trong hai đề sau đây: ĐỀ 1:
Câu 4. (1,0 điểm) Giải phương trình 4 2
x − x −12 = 0. (1) Lời giải Đặt 2
x = t (t ≥ 0) , phương trình (1) trở thành: 2t − t −12 = 0.
Ta có: 2t − t −12 = 0. Ta có: ∆ = (− )2 1 − 4.( 12
− ) = 49 > 0 ⇒ ∆ = 7 , nên phương trình có hai nghiệm phân biệt 1+ 7 t = = 4 (N ) 2 1− 7 t = = 3 − (L) 2 x = 2 Với 2
t = 4 ⇒ x = 4 ⇔ x = 2 −
Vậy phương trình có tập nghiệm là: S = { 2; − } 2
Câu 5. (1,0 điểm) Sân vận động Quốc gia Mỹ Đình (Quận Nam Từ Liêm – Hà Nội) có mặt sân bóng
đá hình chữ nhật với chiều dài hơn chiều rộng 37m và có diện tích là 2
7140m . Hãy tính chiều
dài và chiều rộng của mặt sân bóng đá này. Lời giải
Gọi chiều rộng của mặt sân là x (m) ( x > 0).
Suy ra chiều dài mặt sân là x + 37 (m) .
Vì diện tích mặt sân là 2
7140m nên ta có phương trình x(x + ) 2
37 = 7140 ⇔ x + 37x − 7140 = 0 Ta có: 2 ∆ = 37 − 4.( 7140 − ) = 29929 > 0, ∆ =173 37 − +173 x = = 68 (N)
Suy ra phương trình có 2 nghiệm phân biệt 2 37 − − 173 x = = 105 − (L) 2
Vậy chiều rộng của mặt sân là 68m, chiều dài của mặt sân là 68 + 37 =105 (m)
Câu 6. (1,0 điểm) Cho phương trình 2
x − mx + m −1 = 0.(m là tham số). Tìm các giá trị của m để phương
trình có hai nghiệm phân biệt x , x thỏa mãn 2 2 + = + . 1 2 x x x x 1 2 1 2 Lời giải
Ta có: ∆ = (−m)2 − (m − ) 2 4
1 = m − 4m + 4 = (m − 2)2 .
Phương trình có hai nghiệm phân biệt x , x ⇔ ∆ > 0 ⇔ (m − 2)2 > 0 ⇔ m − 2 ≠ 0 ⇔ m ≠ 2 1 2 Trang 4
x + x = m
Theo hệ thức Vi – ét, ta có: 1 2
x .x = m − 1 1 2 Theo đề ta có 2 2
x + x = x + x 1 2 1 2
⇔ (x + x )2 − 2x x − x + x = 0 1 2 1 2 ( 1 2) 2
⇔ m − 2(m − ) 1 − m = 0 2
⇔ m − 2m + 2 − m = 0 2
⇔ m − 3m + 2 = 0 m =1 (n)
⇔ m = 2 (l) Vậy m =1. ĐỀ 2:
Câu 4. (1,0 điểm) Giải phương trình 2
2x − 5x + 2 = 0. Lời giải 5 + 3 x = = 2 Ta có: ∆ = (− )2
5 − 4.2.2 = 9 > 0 nên phương trình có 2 nghiệm phân biệt 2.2 5 − 3 1 x = = 2.2 2
Vậy phương trình có tập nghiệm 1 S 2; = . 2
Câu 5. (1,0 điểm) Một máy giặt và một tivi có giá tổng cộng 28 690 000 đồng. Sau khi giảm 10% một
máy giặt và 15% một tivi, tổng số tiền mua hai sản phẩm này chỉ còn lại 24 961 000 đồng. Tính
giá tiền mỗi sản phẩm trước khi giảm giá. Lời giải
Gọi giá tiền của một máy giặt là x (đồng) (x < 28690000) .
Giá tiền của một ti vi là y (đồng) ( y < 28690000) .
Vì một máy giặt và một tivi có giá tổng cộng 28 690 000 đồng nên ta có phương trình: x + y = 28690000 (1) .
Giá của một máy giặt sau khi giảm giá là 10% là 0,9x (đồng).
Giá của một ti vi sau khi giảm giá là 15% là 0,85x (đồng).
Vì sau khi giảm giá, tổng số tiền mua hai sản phẩm này là 24 961 000 đồng nên ta có phương
trình: 0,9x + 0,85y = 24961000 (2).
Từ (1) và (2) ta có hệ phương trình: x + y = 28690000
0,9x + 0,9y = 25821000 0,05y = 860000 ⇔ ⇔
0,9x 0,85y 24961000
0,9x 0,85y 24961000 + = + =
x + y = 28690000 x =17200000 ⇔ (tmdk) y =11490000 Trang 5
Vậy giá tiền một máy giặt là 11 490 000 đồng; giá tiền của một tivi là 17 200 000 đồng.
Câu 6. (1,0 điểm) Cho biểu thức B = x − 2 x − 2 + 2022 (với x ≥ 2 ). Với giá trị nào của x thì B đạt giá
trị nhỏ nhất? Tính giá trị nhỏ nhất đó. Lời giải Ta có:
B = x − 2 x − 2 + 2022
B = x − 2 − 2 x − 2 +1+ 2023
B = ( x − 2 − )2 1 + 2023 Vì ( x − − )2 2 1 ≥ 0 x
∀ ≥ 2 nên B = ( x − − )2 2 1 + 2023 ≥ 2023, x ∀ ≥ 2.
Dấu “=” xảy ra khi và chỉ khi x − 2 −1 = 0 ⇔ x − 2 =1 ⇔ x − 2 =1 ⇔ x = 3(N) .
Vậy GTNN của B bằng 2023 đạt tại x = 3.
--------------- HẾT ------------- Trang 6
Document Outline
- de-tuyen-sinh-vao-lop-10-mon-toan-nam-2022-2023-so-gddt-tra-vinh
- 59.TRÀ VINH