


Preview text:
Lời giải Bài 1: 5
x 3y 1
1. Giải hệ phương trình:
x 3y 5 2. Cho biểu thức x 3 x 4x 32 P
; x 0, x 16. x 4 x 4 x 16
c) Rút gọn biểu thức P .
d) Tìm giá trị lớn nhất của P . x 1 5
x 3y 1 6x 6 x 1 1. Ta có 4 x 3y 5 5x 3y 1 5.1 3y 1 y 3 2. a) Ta có: x 3 x 4x 32 x 3 x 4x 32 P x 4 x 4 x 16 x 4
x 4 x 4 x 4
x x 4 3 x x 4 4x 32 x 4 x 3x 12 x 4x 32
x 4 x 4
x 4 x 4 8 x x 4 8 32 8
x 4 x 4 x 4 x 4 x 4
b) P lớn nhất x 4 nhỏ nhất x 0 x 0 . Khi đó P 2 .
Vậy giá trị lớn nhất của P là 2. Bài 2: 1 1. 2
x m 3 2
x m 1 0 4 1
Ta có m 32 2 2 2
4( m 1) m 6m 9 m 4 6m 5 4 5
Phương trình có hai nghiệm phân biệt x , x 0 6m 5 0 m * 1 2 6
Khi điều kiện * được thỏa, phương trình có hai nghiệm x , x , theo định lý Vi-et ta có: 1 2
x x m 3 1 1 2 1 2
x x m 1 2 1 2 4 Do đó:
2 x x 2 8x .x 34 2.m 32 1 2 8 m 1 34 1 2 1 2 4 2 2
m 6m 9 2 2m 8 34
12m 24 m 2 (Thoûa (*))
Vậy giá trị cần tìm là m 2 . 2.
a) Đường thẳng d đi qua điểm A 1 ;5 5 . a
1 4 5 a 4 a 9 . 2
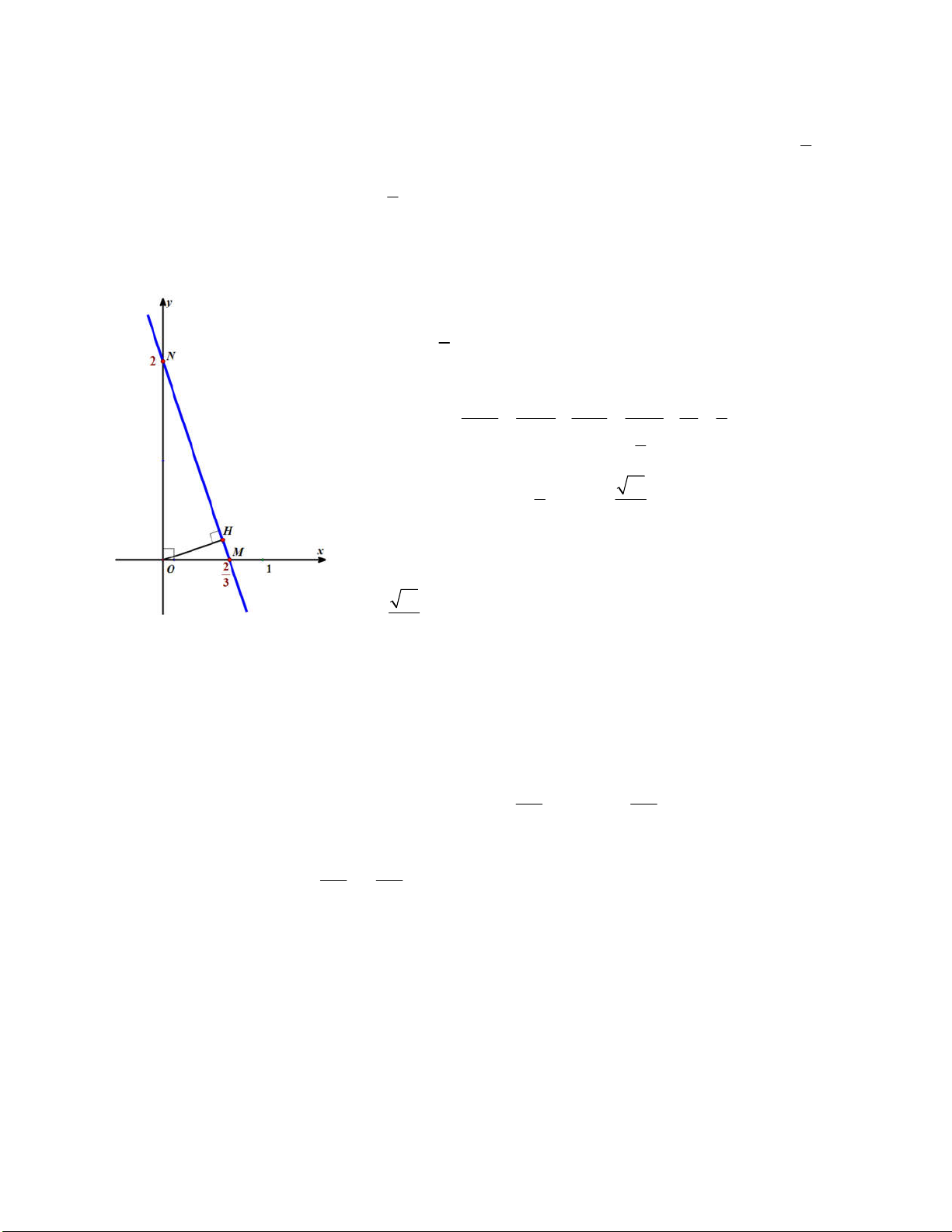
b) Cho y 0 thay vào phương trình đường thẳng d ta được: 0 3x 2 x . 1 3 2 Vậy
d cắt trục hoành tại điểm M ;0 . 1 3
Cho x 0 thay vào phương trình đường thẳng d ta được y 2 . Vậy d cắt trục 1 1
tung tại điểm N 0;2. 2
Ta có OM ,ON 2 . Trong tam giác vuông OMN ta vẽ đường 3 cao OH , khi đó: 1 1 1 1 1 5 2 2 2 2 2 OH OM ON 2 2 2 3 2 10 2
OH OH 5 5
Vậy khoảng cách từ gốc tọa độ O đến đường thẳng d là 1 10 OH 5 Bài 3: Cách 1: Gọi ,
x y lần lượt là số học sinh dự thi của mỗi trường A, B. Điều kiện , x y nguyên dương.
Cả hai trường A và B có tổng số 380 thí sinh dự thi nên: x y 380 1 55 45
Số thí sinh trúng tuyển của trường A và B lần lượt là: x (thí s , inh) y (thí sinh) . 100 100
Số thí sinh trúng tuyển của cả hai trường là 191 thí sinh nên: 55 45 x +
y 191 11x 9y 3820 2 100 100
Từ (1) suy ra y 380 x thay vào (2) ta được: 11x 9380 x 3820 2x 400 x 200
Suy ra y 180 . Vậy số thí sinh dự thi của mỗi trường A, B lần lượt là 200 và 180.
Cách 2: Gọi x là số thí sinh dự thi trường A. Điều kiện: x nguyên dương, x 380 (*)
Số thí sinh dự thi trường B là 380 x . Theo đề bài ta lập được phương trình:
0,55x 0, 45380 x 191 0,1x 20 x 200 (thoûa (*)) y 180
Vậy có 200 thí sinh dự thi trường A và 180 thí sinh dự thi trường B. Bài 4:
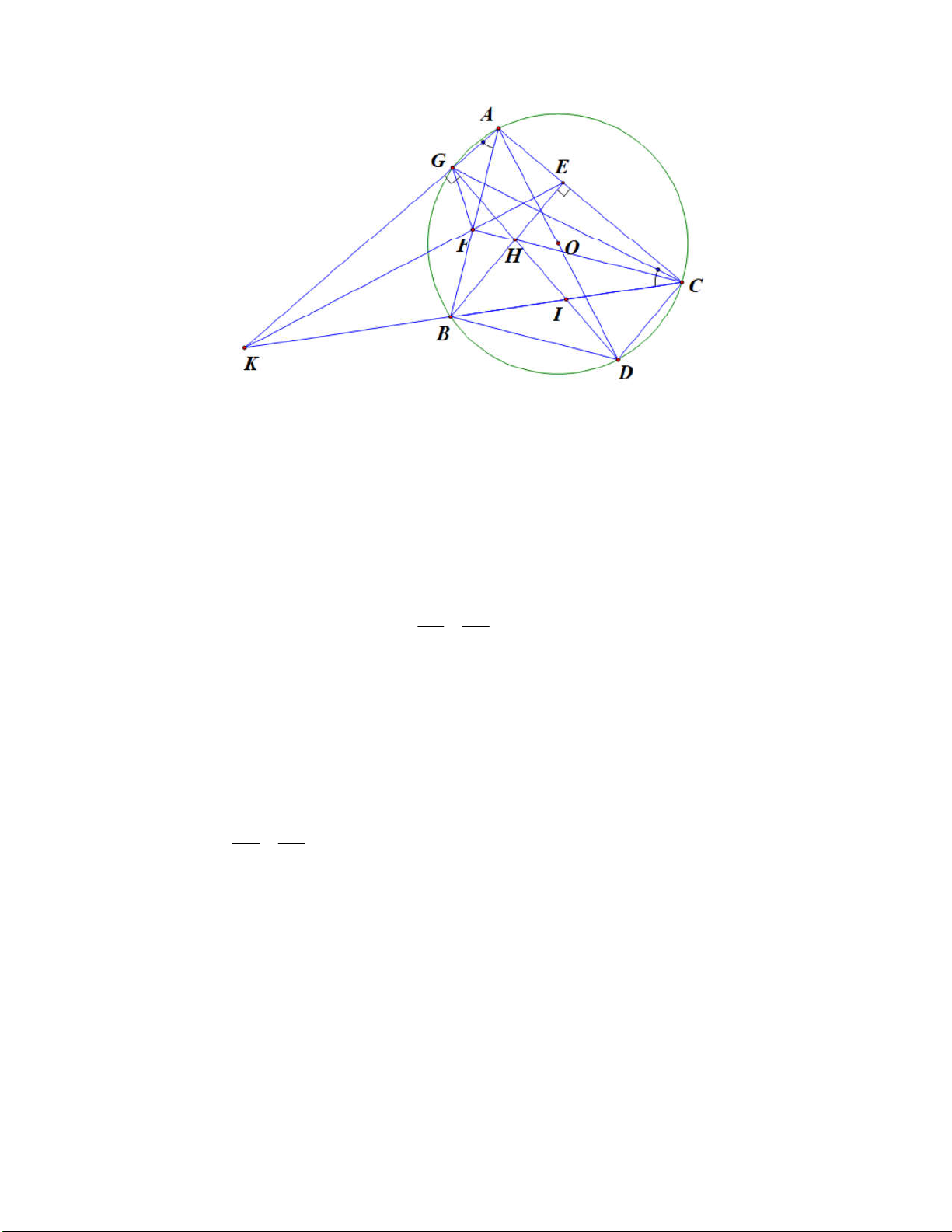
1. BE vaø CF là các đường cao của tam giác ABC nên
BFC BEC 90 . Vậy các điểm
E, F cùng nhìn đoạn BC dưới một góc vuông nên các điểm E, F, , B C cùng nằm trên
đường tròn đường kính BC . Hay tứ giác BCEF nội tiếp.
2. Tứ giác BCEF nội tiếp nên
BCF BEF (góc nội tiếp cùng chắn cung BF ) Ta có
KBF BCF CFB (Goùc ngoaøi tam giaùc) BEF 90 BEF BEC KEC
Xét hai tam giác KBF và KEC ta có:
BKF EKC (Góc chung),
KBF KEC , do đó hai KB KF
tam giác này đồng dạng. Suy ra .
KB KC KF.KE . KE KC Ta có:
AEH AFH 90 4 điểm ,
A E, H , F cùng nằm trên đường tròn đường kính AH .
Xét hai tam giác KAB và KCG :
AKB CKG Góc chung),
KAB KCG (Góc nội tiếp cùng chắn cung BG ) KA KB
Vậy hai tam giác nói trên là đổng dạng do đó: . KG KA .
KB KC KF.KE . KC KG KG KF Suy ra: , kết hợp với
GKF EKA (Góc chung) nên hai tam giác KGF và KEA KE KA đồng dạng. Suy ra
AEK FGK (Góc tương ứng).
Tứ giác AGFE có:
AGF AEF AGF AEK AGF FGK 180 (Kề bù)
Vậy tứ giác AGFE nội tiếp.
Suy ra 5 điểm A, G, F, E, H cùng thuộc một đường tròn đường kính AH.
4. Từ kết quả câu 3. ta suy ra HG AK .
Vẽ đường kính AD khi đó ta có:
DG AK (Góc
DGA nội tiếp chắn nửa đường tròn) Suy ra ,
D H,G thẳng hàng. BH AC BH //DC DC AC
Tương tự ta cũng có CH //BD , suy ra tứ giác BDCH là hình bình hành. Vậy I là trung
điểm cùa HD hay G, H, I, D thẳng hàng. Do đó HI vuông góc với AK .
Bài 5. (1,0 điểm) Cho các số thực dương a, ,
b c thỏa mãn a b c 2024 . Tìm giá trị lớn nhất của a b c biểu thức P .
a 2024a bc
b 2024b ca
c 2024c ab
a b a c
a b c Ta có
a bc a b ca bc a ba c 2 2024 2 2 a a
a abac
a 2024a bc
a abaca abac
a a a ba c 2
a a a ba c a a ba c 2 a 2
a a ba c
ab bc ca
ab bc ca
2a b c 2 a a 2 ab ac
ab bc ca
2ab bc ca b bc ba c ca cb Tương tự ta cũng có: ,
b 2024b ca
2ab bc ca c 2024c ab 2ab bc ca Suy ra: a b c ab ac bc ba ca cb P
a 2024a bc
b 2024b ca
c 2024c ab
2ab bc ca 2ab bc ca 2ab bc ca
2ab bc ca
ab bc ca 1 2 2024
Đẳng thức xảy ra a b c 3
Vậy giá trị lớn nhất của P là 1.
Document Outline
- de-tuyen-sinh-vao-lop-10-mon-toan-nam-2023-2024-so-gddt-binh-dinh
- TS_10_23-24




